Ciencias Empresariales
Nombres index
NÚMEROS [Author ID1: at Tue Oct 21 10:43:00 2003 ]NOMBRES [Author ID1: at Tue Oct 21 10:43:00 2003]ÍNDEX
Definició
Els números [Author ID1: at Tue Oct 21 10:43:00 2003 ]nombres [Author ID1: at Tue Oct 21 10:43:00 2003]índex són indicadors de la variació en el temps de determinades variables,[Author ID1: at Tue Oct 21 10:43:00 2003 ] respecte a una de referència donada de forma [Author ID1: at Tue Oct 21 10:43:00 2003 ]manera [Author ID1: at Tue Oct 21 10:43:00 2003]arbitra[Author ID1: at Tue Oct 21 12:00:00 2003 ]à[Author ID1: at Tue Oct 21 12:00:00 2003]ria, denominada període base.
Disposar de la informació en forma percentual permet comparar varies [Author ID1: at Tue Oct 21 10:44:00 2003 ]diverses [Author ID1: at Tue Oct 21 10:44:00 2003]variables, inclòs [Author ID1: at Tue Oct 21 10:44:00 2003 ]fins i tot [Author ID1: at Tue Oct 21 10:44:00 2003]si originalment estan expressades [Author ID1: at Tue Oct 21 10:44:00 2003]en diferent unitat de mesura.
La majoria d'estadístiques macroeconòmiques es donen en forma d'índex [Author ID1: at Tue Oct 21 10:44:00 2003 ]: índex de preus al consumo[Author ID1: at Tue Oct 21 10:44:00 2003 ] (IPC), índex de producció, índex de la borsa, etc.
[Author ID1: at Tue Oct 21 10:44:00 2003 ]Classificació dels números [Author ID1: at Tue Oct 21 10:44:00 2003 ]nombres [Author ID1: at Tue Oct 21 10:44:00 2003]índex
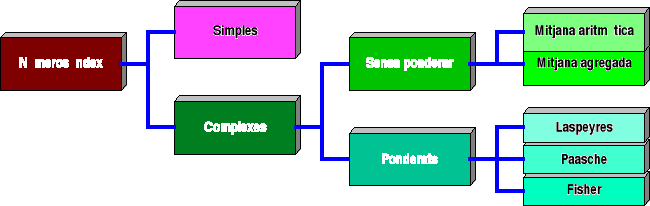
Números [Author ID1: at Tue Oct 21 10:45:00 2003 ]Nombres [Author ID1: at Tue Oct 21 10:45:00 2003]índex simples
| t | yt | Índex S[Author ID1: at Tue Oct 21 10:45:00 2003 ]s[Author ID1: at Tue Oct 21 10:45:00 2003]imple |
| t0 | y0 | (y0 / y0) 100 |
| t1 | y1 | (y1 / y0) 100 |
| . . . | . . . | |
| tn | yn | (yn/ y0) 100 |
Exemple:[Author ID1: at Tue Oct 21 10:45:00 2003] tenim uns preus i calculem l'índex:[Author ID1: at Tue Oct 21 10:45:00 2003]
| Anys | Preus | Índex simple |
| 1999 | 100 | |
| 2000 | 107 | |
| 2001 | 115 | |
| 2002 | 117 |
Interpretació
-
A l[Author ID1: at Tue Oct 21 10:45:00 2003 ]L[Author ID1: at Tue Oct 21 10:45:00 2003]'any 2000 els preus s'[Author ID1: at Tue Oct 21 10:45:00 2003]han incrementat un 7 [Author ID1: at Tue Oct 21 10:45:00 2003]% respecta[Author ID1: at Tue Oct 21 10:45:00 2003 ]e[Author ID1: at Tue Oct 21 10:45:00 2003] als preus de l'any 1999.
-
A l[Author ID1: at Tue Oct 21 10:45:00 2003 ]L[Author ID1: at Tue Oct 21 10:45:00 2003]'any 2001 els preus s'[Author ID1: at Tue Oct 21 10:45:00 2003]han incrementat un 15 [Author ID1: at Tue Oct 21 10:45:00 2003]% respecta[Author ID1: at Tue Oct 21 10:46:00 2003 ]e[Author ID1: at Tue Oct 21 10:46:00 2003] als preus de l'any 1999.
-
Etc.
Números [Author ID1: at Tue Oct 21 10:46:00 2003 ]Nombres [Author ID1: at Tue Oct 21 10:46:00 2003]índex complexos sense ponderar
S'utilitzen quan tenim més d'una variable i es vol estudiar la variació conjunta d'aquest grup de variables en el temps.
Mètode de la mitjana aritmètica simple. Índex de Sauerbeck
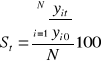
Exemple: tenim els preus de 2 articles i calculem l'índex de Sauerbeck.[Author ID1: at Tue Oct 21 11:28:00 2003]
| Any | p1 | p2 | p3 | Ip1 | Ip2 | Ip3 | St |
| 1999 | 350 | 200 | 540 | 100 | 100 | 100 | 100 |
| 2000 | 365 | 210 | 560 | 104 | 105 | 103,7 | 104,3 |
| 2001 | 369 | 215 | 572 | 105 | 108 | 105,9 | 106,3 |
| 2002 | 372 | 218 | 580 | 106 | 109 | 107,4 | 107,6 |
![]()
![]()
![]()
![]()
Interpretació
Igual que l'índex simple.
Mètode de la mitjana agregada simple. Índex de Bradstreet-D*tot
Se sumen primer els valors de les se[Author ID1: at Tue Oct 21 11:29:00 2003 ]è[Author ID1: at Tue Oct 21 11:29:00 2003]ries i es calcula l'índex simple de la sèrie agregada.
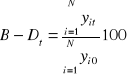
| Any | p1 | p2 | p3 | p1+ p2+ p3 | B-Dt |
| 1999 | 350 | 200 | 540 | 1090 | 100,0 |
| 2000 | 365 | 210 | 560 | 1135 | 104,1 |
| 2001 | 369 | 215 | 572 | 1156 | 106,1 |
| 2002 | 372 | 218 | 580 | 1170 | 107,3 |
![]()
Interpretació
Igual que l'índex simple.
Índexs[Author ID1: at Tue Oct 21 11:35:00 2003] complexos ponderats de preus i quantitats. Índex de Laspeyres, Paasche i Fisher.[Author ID1: at Tue Oct 21 11:35:00 2003 ]
S'utilitzen per obtenir un índex complex que,[Author ID1: at Tue Oct 21 11:35:00 2003] al mateix temps que sintetitza diferents variables observades, recull la diferent importància de cada una d'elles[Author ID1: at Tue Oct 21 11:35:00 2003 ].
S'estudien bàsicament se[Author ID1: at Tue Oct 21 11:35:00 2003 ]è[Author ID1: at Tue Oct 21 11:35:00 2003]ries que inclouen les variables preus i quantitats.
Índex de Laspeyres
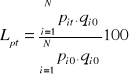
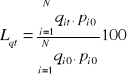
Avantatges d'aquest índex
-
Aïlla l'evolució de la variable ja que la ponderació és fixa.
-
Necessita poca informació.
Inconvenients
-
A mesura que ens alluny[Author ID1: at Tue Oct 21 12:02:00 2003]em de l'any base,[Author ID1: at Tue Oct 21 11:37:00 2003] les ponderacions són cada cop menys representatives de la realitat, queden desfasades.
És l'índex que s'[Author ID1: at Tue Oct 21 11:37:00 2003]e [Author ID1: at Tue Oct 21 11:37:00 2003 ]utilitza per confeccionar les magnituds macroeconòmiques: índex de preus, de la borsa, etc.
Exemple: T[Author ID1: at Tue Oct 21 11:37:00 2003 ]t[Author ID1: at Tue Oct 21 11:37:00 2003]enim els preus de 3 articles i les quantitats del primer any.
| Any | p1 | q1 | p2 | q2 | p3 | q3 | Lp |
| 1999 | 500 | 20 | 800 | 12 | 400 | 30 | 100,00 |
| 2000 | 540 | 830 | 450 | 108,42 | |||
| 2001 | 590 | 850 | 500 | 117,09 | |||
| 2002 | 620 | 860 | 530 | 122,22 |
Interpretació
Igual que l'índex simple.
Índex de Paasche


Avantatja[Author ID1: at Tue Oct 21 11:38:00 2003 ]ge[Author ID1: at Tue Oct 21 11:38:00 2003] d'aquest índex
-
La[Author ID1: at Tue Oct 21 11:38:00 2003 ]e[Author ID1: at Tue Oct 21 11:38:00 2003]s ponderacions són sempre actuals.
Inconvenients
-
Al variar cada any, [Author ID1: at Tue Oct 21 11:38:00 2003 ]Com que [Author ID1: at Tue Oct 21 11:38:00 2003]tant [Author ID1: at Tue Oct 21 11:38:00 2003 ]els [Author ID1: at Tue Oct 21 11:38:00 2003]preus com les [Author ID1: at Tue Oct 21 11:38:00 2003]quantitats varien cada any[Author ID1: at Tue Oct 21 11:39:00 2003], l'índex [Author ID1: at Tue Oct 21 11:39:00 2003]no aïlla l'efecte de la variació d'[Author ID1: at Tue Oct 21 11:39:00 2003]e [Author ID1: at Tue Oct 21 11:39:00 2003 ]una variable.
-
E[Author ID1: at Tue Oct 21 11:39:00 2003 ]É[Author ID1: at Tue Oct 21 11:39:00 2003]s molt més costos, [Author ID1: at Tue Oct 21 11:39:00 2003 ]necessita més informació.
Exemple: T[Author ID1: at Tue Oct 21 11:39:00 2003 ]t[Author ID1: at Tue Oct 21 11:39:00 2003]enim els preus de 3 articles i les quantitats de tots els anys.
| Any | p1 | q1 | p2 | q2 | p3 | q3 | Pp |
| 1999 | 500 | 20 | 800 | 12 | 400 | 30 | 100,00 |
| 2000 | 540 | 25 | 830 | 14 | 450 | 36 | 108,45 |
| 2001 | 590 | 28 | 850 | 15 | 500 | 38 | 117,16 |
| 2002 | 620 | 22 | 860 | 13 | 530 | 40 | 123,05 |
![]()
![]()
![]()
![]()
Interpretació
Igual que l'índex simple.
Índex de Fisher[Author ID1: at Tue Oct 21 11:41:00 2003]


No té cap avantatja[Author ID1: at Tue Oct 21 11:41:00 2003 ]ge[Author ID1: at Tue Oct 21 11:41:00 2003] especial.
Exemple: U[Author ID1: at Tue Oct 21 11:41:00 2003 ]u[Author ID1: at Tue Oct 21 11:41:00 2003]tilitzem els índexs[Author ID1: at Tue Oct 21 11:41:00 2003] ja calculats en els apartats anteriors.
| Any | Lp | Pp | Fp |
| 1999 | 100,00 | 100,00 | 100,00 |
| 2000 | 108,42 | 108,45 | 108,43 |
| 2001 | 117,09 | 117,16 | 117,12 |
| 2002 | 122,22 | 123,05 | 122,63 |
Interpretació
Igual que l'índex simple.
Canvi del període base
Sempre podem tenir l'índex amb base [Author ID1: at Tue Oct 21 11:42:00 2003 ]a[Author ID1: at Tue Oct 21 11:41:00 2003 ]segons [Author ID1: at Tue Oct 21 11:42:00 2003] [Author ID1: at Tue Oct 21 11:42:00 2003 ]l'any que ens convingui fent[Author ID1: at Tue Oct 21 11:41:00 2003] un canvi de base.
Exemple: tenim uns índexs[Author ID1: at Tue Oct 21 11:41:00 2003] calculats en base a [Author ID1: at Tue Oct 21 11:42:00 2003 ]segons [Author ID1: at Tue Oct 21 11:42:00 2003]un any i fem un canvi a un altre any base.
| Anys | Índex (base=1999) | Índex (base=2002) |
| 1999 | 100 | (100/120) 100 = 83,3 |
| 2000 | 107 | (107/120) 100 = 89,2 |
| 2001 | 115 | (115/120) 100 = 95,8 |
| 2002 | 120 | (120/120) 100 = 100 |
Renovació i enllaç
La necessitat de renovació ve donada pels [Author ID1: at Tue Oct 21 11:43:00 2003 ]és deguda als [Author ID1: at Tue Oct 21 11:43:00 2003]canvis en l'[Author ID1: at Tue Oct 21 11:43:00 2003]a [Author ID1: at Tue Oct 21 11:43:00 2003 ]activitat;[Author ID1: at Tue Oct 21 11:43:00 2003 ]:[Author ID1: at Tue Oct 21 11:43:00 2003] productes que desapareixen, altres que [Author ID1: at Tue Oct 21 11:43:00 2003 ]apareixen, etc.
En aquest cas,[Author ID1: at Tue Oct 21 11:43:00 2003] hi ha dues sèries diferents que cal unir en una de sola.
En el següent [Author ID1: at Tue Oct 21 11:43:00 2003 ]l'[Author ID1: at Tue Oct 21 11:43:00 2003]exemple següent [Author ID1: at Tue Oct 21 11:43:00 2003]tenim uns índexs[Author ID1: at Tue Oct 21 11:43:00 2003] de preus ja calculats, utilitzant un nou mètode a partir de l'any 1998. Es crea una única sèrie fent[Author ID1: at Tue Oct 21 11:43:00 2003] un canvi de base.
| Anys | Índex (base = 1996) | Índex (base = 1999) | Nova sèrie (base=1999) |
| 1996 | 100 | (100/120)100= 83 | |
| 1997 | 105 | (105/120)100= 87 | |
| 1998 | 112 | (112/120)100= 93 | |
| 1999 | 120 | 100 | 100 |
| 2000 | 106 | 106 | |
| 2001 | 111 | 111 | |
| 2002 | 116 | 116 |
Deflació de les sè[Author ID1: at Tue Oct 21 11:43:00 2003]e[Author ID1: at Tue Oct 21 11:43:00 2003 ]ries temporals de valor
Les se[Author ID1: at Tue Oct 21 11:44:00 2003 ]è[Author ID1: at Tue Oct 21 11:44:00 2003]ries temporals expressades en xifres monetàries,[Author ID1: at Tue Oct 21 11:44:00 2003 ] estan sotmeses a les fluctuacions del poder adquisitiu de la moneda.
-
El valor nominal (VN) és la xifra monetària observada (moneda corrent).
-
El valor real (VR) és esta [Author ID1: at Tue Oct 21 11:44:00 2003 ]aquesta [Author ID1: at Tue Oct 21 11:44:00 2003]xifra un cop efectuada [Author ID1: at Tue Oct 21 11:44:00 2003 ]feta [Author ID1: at Tue Oct 21 11:44:00 2003]la correcció convenient per eliminar l'[Author ID1: at Tue Oct 21 11:44:00 2003 ]a [Author ID1: at Tue Oct 21 11:44:00 2003]influe[Author ID1: at Tue Oct 21 11:44:00 2003 ]è[Author ID1: at Tue Oct 21 11:44:00 2003]ncia de la depreciació monetària (moneda constant).
Deflactar una sèrie cronològica és convertir els valors nominals en reals.
Utilitat. Quan es fa un estudi utilitzant una sèrie cronològica de valor,[Author ID1: at Tue Oct 21 11:51:00 2003] s'utilitza la sèrie en valor constant per tal [Author ID1: at Tue Oct 21 11:51:00 2003 ]que[Author ID1: at Tue Oct 21 11:51:00 2003 ]è[Author ID1: at Tue Oct 21 11:51:00 2003] els valors siguin comparables.
Per obtenir els valors reals es fa la següent [Author ID1: at Tue Oct 21 11:51:00 2003 ]fo[Author ID1: at Tue Oct 21 12:04:00 2003 ]ó[Author ID1: at Tue Oct 21 12:04:00 2003]rmula següent[Author ID1: at Tue Oct 21 11:51:00 2003]:
![]()
Amb números [Author ID1: at Tue Oct 21 11:51:00 2003 ]nombres [Author ID1: at Tue Oct 21 11:51:00 2003]índex:[Author ID1: at Tue Oct 21 12:04:00 2003] ![]()
L'IVN (índex del valor nominal) i l'IPC han d'estar en base al [Author ID1: at Tue Oct 21 11:51:00 2003 ]de partir del [Author ID1: at Tue Oct 21 11:51:00 2003]mateix any per poder calcular l'IVR (índex del valor real).
Exemple: tenim uns salaris anuals (VN) i l'IPC i calcularem: V[Author ID1: at Tue Oct 21 11:51:00 2003 ]v[Author ID1: at Tue Oct 21 11:51:00 2003]alor real (VR), l'[Author ID1: at Tue Oct 21 12:07:00 2003 ]índex de salaris amb valors nominals (IVN) i valors reals (IVR).[Author ID1: at Tue Oct 21 12:07:00 2003]
| Any | VN | IPC | IPC(95) | VR | IVN | IVR |
| 1996 | 135 | 100,0 | 1250,0 | 100,0 | 100,0 | |
| 1997 | 140 | 103,7 | 1234,3 | 102,4 | 98,7 | |
| 1998 | 148 | 109,6 | 1185,8 | 104,0 | 94,9 | |
| 1999 | 152 | 112,6 | 1243,4 | 112,0 | 99,5 | |
| 2000 | 156 | 115,6 | 1263,5 | 116,8 | 101,1 | |
| 2001 | 159 | 117,8 | 1350,0 | 127,2 | 108,0 | |
| 2002 | 163 | 120,7 | 1341,7 | 129,6 | 107,3 |
Càlculs que s'han de fer[Author ID1: at Tue Oct 21 11:52:00 2003]a[Author ID1: at Tue Oct 21 11:52:00 2003 ] realitzar[Author ID1: at Tue Oct 21 12:07:00 2003 ]:
-
Canvi de base de l'IPC.
-
Per calcular el valor real, es divideix el valor nominal per l'IPC (base [Author ID1: at Tue Oct 21 11:52:00 2003]= [Author ID1: at Tue Oct 21 11:52:00 2003]1995),[Author ID1: at Tue Oct 21 11:52:00 2003 ] i es multiplica per 100.
L'[Author ID1: at Tue Oct 21 11:52:00 2003]a [Author ID1: at Tue Oct 21 11:52:00 2003 ]evolució dels índexs[Author ID1: at Tue Oct 21 11:52:00 2003] en valor nominal és superior a l'evolució en valor real. Durant uns anys el valor real és inferior a 100. Aquesta persona ha perdut poder adquisitiu, malgrat l'increment del seu salari. Els darrers anys hi ha un increment del salari i del valor adquisitiu perquè l'índex del valor real supera el valor 100.
Índex de preus al consum (IPC)
l[Author ID1: at Tue Oct 21 11:53:00 2003 ]L[Author ID1: at Tue Oct 21 11:53:00 2003]'IPC mesura l'evolució en el temps dels preus d'un conjunt determinat de be[Author ID1: at Tue Oct 21 11:53:00 2003 ]é[Author ID1: at Tue Oct 21 11:53:00 2003]ns i serveis,[Author ID1: at Tue Oct 21 11:53:00 2003 ] que formen part de la cistella de la compra (conjunt de be[Author ID1: at Tue Oct 21 11:53:00 2003 ]é[Author ID1: at Tue Oct 21 11:53:00 2003]ns i serveis que les famílies compren habitualment).
S'utilitza per calcular l'increment que han d'experimentar els salaris cada any. L'elabora l'Institut Nacional d'Estadística.
Grups
Aliments, begudes i tabac.
Vestit i calçat.
Habitatge.
Parament i serveis de la llar.
Serveis metges [Author ID1: at Tue Oct 21 11:54:00 2003 ]mèdics [Author ID1: at Tue Oct 21 11:54:00 2003]i conservació de la salut.
Transports i comunicacions.
Oci, cultura i ensenyament.
Altres despeses de consum.
La cistella de la compra s'obté mitjançant l'E[Author ID1: at Tue Oct 21 11:59:00 2003 ]e[Author ID1: at Tue Oct 21 11:59:00 2003]nquesta de P[Author ID1: at Tue Oct 21 11:59:00 2003 ]p[Author ID1: at Tue Oct 21 11:59:00 2003]ressupostos F[Author ID1: at Tue Oct 21 11:59:00 2003 ]f[Author ID1: at Tue Oct 21 11:59:00 2003]amiliars,[Author ID1: at Tue Oct 21 11:59:00 2003] que es fa a una mostra significativa de famílies del país. La selecció de les famílies es realitza en base a [Author ID1: at Tue Oct 21 11:59:00 2003 ]fa d'acord amb [Author ID1: at Tue Oct 21 11:59:00 2003]criteris qualitatius (grandària, tipus de habitatge, etc.) i quantitatius (nivell d'ingressos mínims o màxims, etc.) o amb una combinació d'ambdós.
[Author ID2: at Tue Jul 27 16:08:00 2004 ][Author ID2: at Tue Jul 27 16:08:00 2004 ][Author ID2: at Tue Jul 27 16:08:00 2004 ]41[Author ID2: at Tue Jul 27 16:08:00 2004 ][Author ID2: at Tue Jul 27 16:08:00 2004 ]

Descargar
| Enviado por: | Jamgaci |
| Idioma: | catalán |
| País: | España |
