Equipos e instalaciones electrotécnicas
Multiplexores y demultiplexores
Memoria 4
Multiplexores
Demultiplexores
Circuitos Comparadores
Circuitos Aritmeticos
Circuitos Multiplexores
Circuitos que envían por un solo canal de salida alguna de las informaciones presentes en varias lineas de salida
N S
Entradas Salidas
| N= 2n |
D0
| a | b | c | s |
| 0 | 0 | 0 | d0 |
| 0 | 0 | 1 | d1 |
| 0 | 1 | 0 | d2 |
| 0 | 1 | 1 | d3 |
| 1 | 0 | 0 | d4 |
| 1 | 0 | 1 | d5 |
| 1 | 1 | 0 | d6 |
| 1 | 1 | 1 | d7 |
D1
D2
D3
D4 S
D5
D6
D7
A B C
Circuito multiplexor en cascada
Ejemplo: Hacer un multiplexor de 8 entradas con multiplexores de 4 entradas
d0
d1 S1
d2
d3
E1
a b S0
E2
d4
d5 S2 C
d6
d7
a b
Estudio del multiplexor 74151 con 8 entradas
Simbolo Lógico
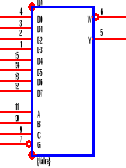
Diagrama de conexiones
Entradas de datos Selección de datos
Vcc 4 5 6 7 A B C
d4 d5 d6 d7 a b
d3 c
d2 d1 d0 y w S
3 2 1 0 Y W strobe
Entradas de datos Salidas
Tabla de la verdad
| C | B | A | strobe | d0 | d1 | d2 | d3 | d4 | d5 | d6 | d7 | y | w |
| x | x | x | 1 | x | x | x | x | x | x | x | x | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | x | x | x | x | x | x | x | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | x | 1 | 0 |
| 0 | 0 | 1 | 0 | x | 0 | x | x | x | x | x | x | 0 | 1 |
| 0 | 0 | 1 | 0 | x | 1 | x | x | x | x | x | x | 1 | 0 |
| 0 | 1 | 0 | 0 | x | x | 0 | x | x | x | x | x | 0 | 1 |
| 0 | 1 | 0 | 0 | x | x | 1 | x | x | x | x | x | 1 | 0 |
| 0 | 1 | 1 | 0 | x | x | x | 0 | x | x | x | x | 0 | 1 |
| 0 | 1 | 1 | 0 | x | x | x | 1 | x | x | x | x | 1 | 0 |
| 1 | 0 | 0 | 0 | x | x | x | x | 0 | x | x | x | 0 | 1 |
| 1 | 0 | 0 | 0 | x | x | x | x | 1 | x | x | x | 1 | 0 |
| 1 | 0 | 1 | 0 | x | x | x | x | x | 0 | x | x | 0 | 1 |
| 1 | 0 | 1 | 0 | x | x | x | x | x | 1 | x | x | 1 | 0 |
| 1 | 1 | 0 | 0 | x | x | x | x | x | x | 0 | x | 0 | 1 |
| 1 | 1 | 0 | 0 | x | x | x | x | x | x | 1 | x | 1 | 0 |
| 1 | 1 | 1 | 0 | x | x | x | x | x | x | x | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | x | x | x | x | x | x | x | 1 | 1 | 0 |
Conclusiones
Como se puede ver en la tabla de la verdad la entrada Strobe está a 0 siempre por lo tanto lo vamos a colocar en 0v del entrenador para ahorrar un interruptor.
La W es la negada de la Y, la casa que construye este circuito es la única que da 2 salidas, todas las otras dan una unia salida de datos, esta opción te permite ahorrar el tener que poner otro circuito integrado inversor.
Circuitos demultiplexores
Utilizan la función inversa de los demultiplexores. La información de la entrada se transmite a la línea de salida seleccionada mediante las entradas de control.
S0
S1
Entrada
S2
S3
A B
| a | b | S0 | S1 | S2 | S3 |
| 0 | 0 | x | 0 | 0 | 0 |
| 0 | 1 | 0 | x | 0 | 0 |
| 1 | 0 | 0 | 0 | x | 0 |
| 1 | 1 | 0 | 0 | 0 | x |
Estudio del demultiplexor 74138 con 1 entrada y 8 salidas.
Simbolo Lógico
Entradas de datos
4 5 6
bits de control
1 2 3 1 2 3
A0 A1 A2
D0 D1 D2 D3 D4 D5 D6 D7
15 14 13 12 11 10 9 7
salidas de datos
Diagrama de conexiones
16 15 14 13 12 11 10 9
Vcc D0 D1 D2 D3 D4 D5 D6
A0 A1 A2 E1 E2 E3 D7
1 2 3 4 5 6 7 8
Tabla de la verdad
| E1 | E2 | E3 | A0 | A1 | A2 | D0 | D1 | D2 | D3 | D4 | D5 | D6 | D7 |
| 1 | x | x | x | x | x | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x | 1 | x | x | x | x | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x | x | 0 | x | x | x | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Conclusiones
Este circuito hace la función inversa del multiplexor. Dos de sus entradas de datos són negadas, por lo tanto las conectaremos a la massa de 5v del entrenador para poder conseguir 1.
Circuitos Comparadores
Compara 2 combinaciones binarias y nos dice si son iguales o no.
| a | b | A=B | A B | A B |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| A1 | A0 | B1 | B0 | |||
| 0 | 0 | 1 | 0 | A0,1= B1,0 | ||
| 0 | 1 | 0 | 1 | A0,1 B1,0 | ||
| 1 | 0 | 0 | 0 | A0,1 B1,0 | ||
| 1 | 1 | 0 | 1 | A0,1 B1,0 |
Estudio del circuito comparador 7485 con magnitud de 4 bits
Simbolo Lógico
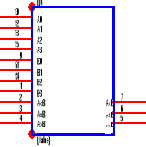
Diagrama de conexiones
Entradas de datos
16 15 14 13 12 11 10 9
Vcc
A3 B2 A2 A1 B1 A0
B3 B0
A B A=B A B A B A=B A B
Gnd
1 2 3 4 5 6 7 8
Entrada Cascada de Salidas
de datos entradas
Tabla de la verdad
| A3,B3 | A2,B2 | A1,B1 | A0,B0 | A B | A B | A=B | A B | A B | A=B |
| A3 B3 | x | x | x | x | x | x | 1 | 0 | 0 |
| A3 B3 | x | x | x | x | x | x | 0 | 1 | 0 |
| A3=B3 | A2 B2 | x | x | x | x | x | 1 | 0 | 0 |
| A3=B3 | A2 B2 | x | x | x | x | x | 0 | 1 | 0 |
| A3=B3 | A2=B2 | A1 B1 | x | x | x | x | 1 | 0 | 0 |
| A3=B3 | A2=B2 | A1 B1 | x | x | x | x | 0 | 1 | 0 |
| A3=B3 | A2=B2 | A1=B1 | A0 B0 | x | x | x | 1 | 0 | 0 |
| A3=B3 | A2=B2 | A1=B1 | A0 B0 | x | x | x | 0 | 1 | 0 |
| A3=B3 | A2=B2 | A1=B1 | A0=B0 | 1 | 0 | 0 | 1 | 0 | 0 |
| A3=B3 | A2=B2 | A1=B1 | A0=B0 | 0 | 1 | 0 | 0 | 1 | 0 |
| A3=B3 | A2=B2 | A1=B1 | A0=B0 | 0 | 0 | 1 | 0 | 0 | 1 |
| A3=B3 | A2=B2 | A1=B1 | A0=B0 | x | x | 1 | 0 | 0 | 1 |
| A3=B3 | A2=B2 | A1=B1 | A0=B0 | 1 | 1 | 0 | 0 | 0 | 0 |
| A3=B3 | A2=B2 | A1=B1 | A0=B0 | 0 | 0 | 0 | 1 | 1 | 0 |
Conclusiones
Las 3 salidas de datos se utilizarán más adelante para hacer el circuito en cascada, donde se conectaran a las entradas del otro circuito.
Si nosotros ponemos el A3 más grande que el B3, en la salida se encenderà la salida de A3 B3. I asi en cada uno de los casos que se puedan encontrar en funcion de la tabla de la verdad.
Estudio del 7485 en casacada.
siempre a 1
A3 A2 A1 A0 B3 B2 B1 B0 A7 A6 A5 A4 B7 B6 B5 B4
A=B A=B A=B
A B A B A B
A B A B A B
A=B A B A B
=
A7 A6 A5 A4 A3 A2 A1 A0 B7 B6 B5 B4 B3 B2 B1 B0
A=B A B A B
Circuitos aritmeticos
Són circuitos convinacionales que realizan operaciones matematicas.
Suma
| A | B | s | cy |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 |
Reta
| A | B | r | borrow |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Estudio del circuito 7483, sumador completo binario de 4 bits con arrastre rapido.
Simbolo Lógico
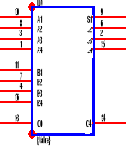
Diagrama de conexiones
16 15 14 13 12 11 10 9
B4 S4 C4 Cin GND B1 A1 S1
A4 S3 A3 B3 VCC S2 B2 A2
1 2 3 4 5 6 7 8
Tabla de la verdad
| Entradas | Salidas | ||||||||
| Cin=0 C2= 0 | Cin=1 C2= 1 | ||||||||
| A1/A3 | B1/B3 | A2/A4 | B2/B4 | S1/S3 | S2/S4 | C2/C4 | S1/S3 | S2/S3 | C2/C4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
Sumador Total
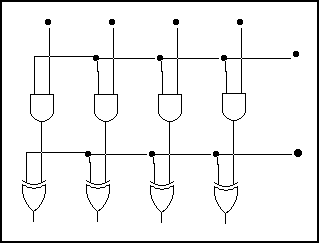
B0 B1 B2 B3
E
W
A0 A1 A2 A3
Cin
Cout
S1 S2 S3 S4
| E | W | Ci |
|
| 0 | 0 | 0 | A |
| 1 | 0 | 0 | A+B |
| 1 | 1 | 0 | A+B |
| 1 | 1 | 1 | A-B |
Descargar
| Enviado por: | Eduard Martínez |
| Idioma: | castellano |
| País: | España |
