Ingeniero en Electrónica
Medición de la potencia activa trifásica equilibrada con carga inductiva
Objeto del ensayo: Debido al tipo de carga la potencia activa deberá ser medida mediante un wattimetro. La conexión a utilizar permitirá determinar la potencia activa consumida por una fase. Como el sistema es trifasico y equilibrado se multiplica por 3 la lectura del wattimetro para obtener la potencia total.
Además para conocer el factor de potencia se determinara la potencia aparente mediante voltímetro y amperímetro.
Como carga se utilizara un motor asincronico trifasico, con el cual se podrán realizar las conexiones en estrella y en triángulo, aplicando las tensiones que correspondan de acuerdo a la chapa de características. Finalmente se trazaran los diagramas vectoriales trifasicos respetando el ángulo µ.
Programa de ensayo: 1) Variar las conexiones en estrella y en triángulo, 2) Medir Uf, If y Pf, 3) Calcular la potencia activa total y la potencia aparente por fase, para ambas conexiones, 4) Determinar el coseno µ y el ángulo µ para las dos conexiones, 5) Trazar o representar los diagramas vectoriales correspondientes a las dos conexiones utilizadas.
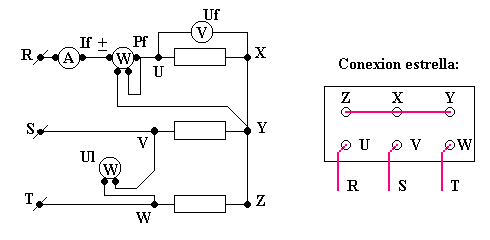
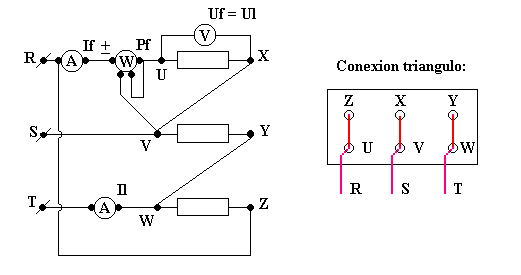
Esquema de conexiones:
Consideración teórica: Recordemos que el consumo de potencia activa por fase en corriente alterna se expresa, Pf = Uf . If . cosµ, donde el ángulo µ es el desfasaje entre la tensión y la corriente y depende del tipo de carga inductiva, capacitiva o valores intermedios conectados en esa fase. Por lo tanto en un sistema trifasico, equilibrado y simétrico, la potencia total esta dada por la expresión Ptrif = 3Pf . If . cosµ. Si reemplazamos los valores de tensión e intensidad de fase por los correspondientes valores compuestos o en línea, obtendremos para las conexiones en estrella y en triángulo las siguientes expresiones:
Estrella - Ptrif = 3 . ( U1/ 3 ) . I1 . cosµ = 3 . Ul . Il . cosµ.
Triángulo - Ptrif = 3 . Ul . ( Il / 3 ) .cosµ = 3 . Ul . Il .cosµ.
En la practica los valores de fase se distinguen con el subíndice “f”, no así los valores de línea por lo tanto:
Ptrif = 3 . U . I cosµ
Este se denomina expresión generalizada de la potencia activa trifasica en sistemas equilibrados y simétricos.
En el caso de carga desequilibrada la expresión de la potencia será:
Pt = Uf1 . If1 . cosµ1 + Uf2 . If2 . cosµ2 + Uf3 . If3 . cosµ3
Pt = Pf1 + Pf2 + Pf3
Factor de potencia: Es la relación entre la potencia activa consumida y la potencia aparente suministrada.
De la expresión generalizada podemos obtener el factor de potencia y por lo tanto el ángulo µ para trazar los diagramas vectoriales trifasicos ,ósea:
Cosµ = Pf = Pf
St Uf . If
Cuadro de valores:
| Nº | If (a) | Il (a) | Uf (v) | Ul (v) | Pf (va) | ||
| Div | Cte | Watt | |||||
| 1 | 4,65 | 4,65 | 133 | 225 | 9 | 10 | 90 |
| 2 | 3,4 | 5,8 | 132 | 225 | 6 | 10 | 60 |
| Nº | P trif (w) | Sf (va) | Pf/Sf | p | Conexión utilizada | ||
| 1 | Estrella | ||||||
| 2 | Triángulo |
Representaciones: Utilizando escalas adecuadas, se representara en un gráfico la P activa en función de la intensidad medida (Im) medida y en otro par de ejes la Ref, en función de la I medida.
Descargar
| Enviado por: | Botta |
| Idioma: | castellano |
| País: | Argentina |
