Ciencias Empresariales
Matrices y determinantes
Tema 1: MATRICES Y DETERMINANTES
-
1.1 MATRICES. DEFINICIÓN
-
1.2 OPERACIONES CON MATRICES
-
1.3 MATRICES ESPECIALES
-
1.4 DETERMINANTES. CÁLCULO
-
1.5 DETERMINANTES. PROPIEDADES
-
1.6 DESARROLLO DE UN DETERMINANTE
-
1.7 RANGO DE UNA MATRIZ.
-
1.8 MATRIZ INVERSA
OBJETIVOS
-Aprender a reconocer, utilizar y operar con matrices. Saber resolver tanto ecuaciones como sistemas de ecuaciones lineales cuyos coeficientes sean matrices.
-Reconocer algunas matrices especiales como identidad, simétrica, diagonal, triangular, escalonadas,..…
-Calcular el determinante de una matriz cuadrada de cualquier orden. Conocer y utilizar las propiedades de los determinantes.
-Concepto claro de rango de una matriz. Calcular perfectamente el rango de una matriz de cualquier orden.
1.1DEFINICIÓN DE MATRIZ
Definición.
Se llama matriz en R a todo conjunto ordenado de números reales dispuestos en m-filas y n-columnas.
Se denota
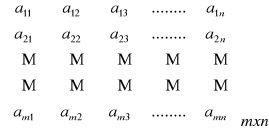
1.2 OPERACIONES CON MATRICES
SUMA
Dadas las matrices A=(aij)mxn B=(bij)mxn se define la suma de A y B a la matriz C=A+B de orden mxn y coeficiente
cij=aij+bij
MULTIPLICACIÓN POR UN ESCALAR
Dada la matriz A=(aij)mxn y el número real α. Se define el producto escalar de α por la matriz A a la matriz B=α A de orden mxn y coeficiente
bij= αaij
PROPIEDADES
Sean α, β ∈ R, A, B, C ∈ Mmxn
1.-(α β)A =α (β A)
2.- 1 A=A
3.- α (A+B)= α A +α B
4.-(α + β) A =αA + βB
PRODUCTO DE MATRICES
Dadas las matrices A=(aij)mxp B=(bij)pxn se define el producto de A por B a la matriz C=A B de orden mxn y coeficiente
PROPIEDADES
1.- A (B C)= (A B) C (Asociativa)
2.- A (B+C) = A B +A C
3.- (A+B) C = A C + B C
4.- A (αB)=(αA) B = α(A B)

MATRICES ESPECIALES
MATRIZ SIMÉTRICA
Una matriz se dice simétrica si y solo si coincide con su transpuesta.
MATRIZ ORTOGONAL
Una matriz cuadrada se dice ortogonal si y solo si su inversa coincide con su transpuesta.
MATRIZ DIAGONAL
Una matriz cuadrada se dice diagonal si y solo si los elementos no situados en su diagonal principal son nulos
MATRIZ TRIANGULAR SUPERIOR
Una matriz cuadrada se dice triangular superior si y solo si los elementos situados por debajo de su diagonal principal son nulos
MATRIZ TRIANGULAR INFERIOR
Una matriz cuadrada se dice triangular inferior si y solo si los elementos situados por encima de su diagonal principal son nulos.
MATRIZ ESCALONADA
Una matriz se dice escalonada, o en forma escalonada, si y solo si el número de ceros anteriores a la primera componente no nula de una fila crece fila por fila hasta llegar a filas en las que todas sus componentes sean nulas
DETERMINANTES. CALCULO
DETERMINANTE DE ORDEN DOS
DETERMINANTE DE ORDEN TRES
PROPIEDADES DE LOS DETERMINANTES
1.- |A| = |At|
2.- Si en una matriz se intercambian entre sí dos filas o columnas consecutivas entonces el determinante cambia de signo.
3.- El determinante de una matriz con una fila o columna toda de ceros es nulo.
4.- El determinante de una matriz con dos filas o columnas iguales es nulo.
5.- El determinante de una matriz con dos filas o columnas proporcionales es nulo.
6.-Si en una matriz una fila o columna es combinación lineal de las restantes, el determinante es nulo.
7.-Si en una matriz se suma a una fila o columna una combinación lineal de las restantes filas o columnas, el determinante de la matriz no varía.
8.-Si en una matriz se multiplican los elementos de una fila o columna por un número real, no nulo, el determinante de la matriz resultante es el determinante de la matriz inicial multiplicado por el número real.
9.-Si en una matriz se descomponen los elementos de una fila o columna como suma de dos sumandos entonces el determinante de la matriz es la suma de los dos determinantes cada uno de ellos con uno de los sumandos en la fila o columna correspondiente
10.- |A B| = |A| |B|
DESARROLLO DE UN DETERMINANTE
MENOR COMPLEMENTARIO
Se llama menor complementario del elemento aik, y se denota Mik, al determinante que se obtiene a partir de una matriz cuadrada eliminando la fila i-ésima y la columna k-ésima
DESARROLLO DE UN DETERMINANTE
RANGO DE UNA MATRIZ
Definición
Dada una matriz A, se llama rango de A, y se denota rg (A), al ORDEN del mayor menor no nulo que se pueda obtener de dicha matriz.
TRANSFORMACIONES QUE CONSERVAN EL RANGO DE UNA MATRIZ
1.- Eliminar una fila o columna toda de ceros.
2.- Suprimir una fila o columna combinación lineal de las restantes.
3.- Multiplicar una fila o columna por un número real no nulo.
4.- Sumar a una fila o columna una combinación lineal de las restantes filas o columnas.
5.- Intercambiar dos filas o columnas
MÉTODOS DE CÁLCULO DEL RANGO DE UNA MATRIZ
A.- POR REDUCCIÓN A UNA MATRIZ ESCALONADA
1.- Reducir la matriz a una matriz escalonada.
2.- Nº filas no nulas = rango de la matriz
B.- POR MENORES
1.- Encontrar un menor de orden 2 no nulo
2.- Se orla con una fila fija y todas las columnas.
2.1 Si algún menor de orden 3 es no nulo. Se repite el paso 2 a partir de ese menor.
2.2 Si todos los menores de orden 3 son nulos entonces se suprime la fila y se orla con otra nueva. Se repite el paso 2
MATRIZ INVERSA
MATRIZ INVERSIBLE
Se dice que una matriz A de orden n es inversible si y solo si existe una matriz B de orden n tal que
A B = B A = I
A la matriz B se la denomina inversa de A y se denota A-1
2

![]()
Descargar
| Enviado por: | Ndz |
| Idioma: | castellano |
| País: | España |
