Matemáticas
Matemáticas
EXAMEN DE FUNCIONS
1. Defineix el concepte de funció, i en relació amb aquest, els conceptes de continuïtat i discontinuïtat, domini, recorregut, creixement i decreixement, màxims i mínims, imatge i antiimatge, signe. On es representa la variable independent? I la dependent?
2. El moviment d'un cotxe és representat per mitjà de la gràfica següent:
És una gràfica d'una funció? Per què?
Quina és la variable independent? I la dependent?
Quina és la imatge de 25? I l'antiimatge de 40?
Entre quins minuts el cotxe ha anat més depressa? Quant temps s'ha aturat?
Digues el recorregut, els intervals de creixement i decreixement, el signe i els extrems locals de la funció
3. Troba el domini de les funcions següents:
a) f(x)= 1/x2-4
b) g(x)= x2-2x+1
c) h(x)= 3x-5/x2+4
4. En les gràfiques següents, digues els intervals de creixement i decreixement, els màxims i mínims relatius, el recorregut i el signe
a)
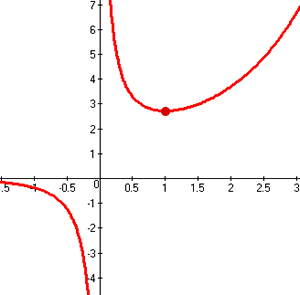
b)
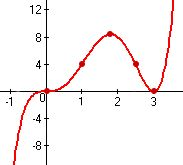
c)
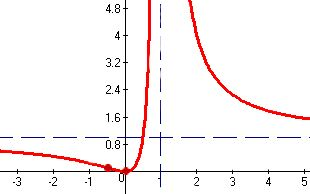
5. Fes una gràfica d'unes funcions que compleixin, com a mínim, els següents requisits:
a) Creixent en (-", -1) i en (1, +" ), decreixent en (-1, 1), convexa en (-", 0) i còncava en (0, +"). Per quina valors de x s'assoleixen els possibles màxims i mínims i punts d'inflexió?
b) Creixent en (-", -2) i en (0, 2), decreixent en (-2, 0) i en (2, +"). Per quins valors s'assoleixen els possibles màxims i mínims?
6. La pressió atmosfèrica disminueix amb l'altura segons es reflecteix a la taula:
| Alçada (m) | 3000 | 4000 | 5000 | 7000 |
| Pressió (kg/cm2) | 700 | 600 | 520 | 400 |
És convenient aplicar aquí la interpolació lineal? Per què?
Troba la pressió atmosfèrica a una alçada de 1500 m
A quina alçada la pressió comença a ser inferior a 570 kg/cm2
7. Donades les funcions f(x)=5x4+x2-1, g(x)=5x2-2x-1 i h(x)= x-1, calcula:
(f· g)(x) + h(x)
f(x) · (g+ h)(x)
f(x) - (g/h)(x)
8. Donades les funcions f(x) i g(x) dels apartats següents, calcula les funcions (g o f) (x) i (f o g) (x) i el domini corresponent :
a) f(x) = 3x-3; g(x)= 5x + 1 c) f(x)= 2x3; g(x)= x2-x
b) f(x)= 1/x; g(x)= x2+1 e) f(x)="x; g(x)= 4x3-x2
9. Les funcions següents s'obtenen fent la composició d'altres dues, troba-les.
a) f(x)= "4x-5 c) h(x)= (2x-1)3
b) g(x)= ln(5x) d) i(x)= 1/x3+5x
10. Representa les següents funcions (en el cas de les paràboles, troba també els punts de tall amb els eixos i el vèrtex)
a) f(x)= x2+1 c) y= x2-2x+1
b) y= x4 d) y= 2x+3
Descargar
| Enviado por: | Alba |
| Idioma: | catalán |
| País: | España |
