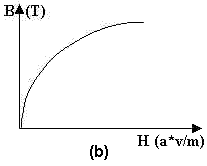Electrónica, Electricidad y Sonido
Magnetismo y electromagnetismo
El Magnetismo
Es uno de los aspectos del electromagnetismo, que es una de las fuerzas fundamentales de la naturaleza. Las fuerzas magnéticas son producidas por el movimiento de partículas cargadas, como por ejemplo electrones, lo que indica la estrecha relación entre la electricidad y el magnetismo. El marco que aúna ambas fuerzas se denomina teoría electromagnética
La manifestación más conocida del magnetismo es la fuerza de atracción o repulsión que actúa entre los materiales magnéticos como el hierro. Sin embargo, en toda la materia se pueden observar efectos más sutiles del magnetismo. Recientemente, estos efectos han proporcionado claves importantes para comprender la estructura atómica de la materia.
El campo mágnetico:
Una barra imantada o un cable que transporta corriente pueden influir en otros materiales magnéticos sin tocarlos físicamente porque los objetos magnéticos producen un `campo magnético'.
Los campos magnéticos suelen representarse mediante `líneas de campo magnético' o `líneas de fuerza'. En cualquier punto, la dirección del campo magnético es igual a la dirección de las líneas de fuerza, y la intensidad del campo es inversamente proporcional al espacio entre las líneas.
En el caso de una barra imantada, las líneas de fuerza salen de un extremo y se curvan para llegar al otro extremo; estas líneas pueden considerarse como bucles cerrados, con una parte del bucle dentro del imán y otra fuera. En los extremos del imán, donde las líneas de fuerza están más próximas, el campo magnético es más intenso; en los lados del imán, donde las líneas de fuerza están más separadas, el campo magnético es más débil. Según su forma y su fuerza magnética, los distintos tipos de imán producen diferentes esquemas de líneas de fuerza. La estructura de las líneas de fuerza creadas por un imán o por cualquier objeto que genere un campo magnético puede visualizarse utilizando una brújula o limaduras de hierro. Los imanes tienden a orientarse siguiendo las líneas de campo magnético. Por tanto, una brújula, que es un pequeño imán que puede rotar libremente, se orientará en la dirección de las líneas. Marcando la dirección que señala la brújula al colocarla en diferentes puntos alrededor de la fuente del campo magnético, puede deducirse el esquema de líneas de fuerza. Igualmente, si se agitan limaduras de hierro sobre una hoja de papel o un plástico por encima de un objeto que crea un campo magnético, las limaduras se orientan siguiendo las líneas de fuerza y permiten así visualizar su estructura.
Los campos magnéticos influyen sobre los materiales magnéticos y sobre las partículas cargadas en movimiento. En términos generales, cuando una partícula cargada se desplaza a través de un campo magnético, experimenta una fuerza que forma ángulos rectos con la velocidad de la partícula y con la dirección del campo. Como la fuerza siempre es perpendicular a la velocidad, las partículas se mueven en trayectorias curvas. Los campos magnéticos se emplean para controlar las trayectorias de partículas cargadas en dispositivos como los aceleradores de partículas o los espectrógrafos de masas.
MAGNETISMO EN CORRIENTE CONTINUA
1.- LEYES FUNDAMENTALES DE CIRCUITOS MAGNÉTICOS
a) Ley de Ampere:
Es la ley básica que rige la producción de campo magnético por medio de una corriente y su ecuación es
ð H * dl = Ineta
Donde H: Intensidad de campo producida por Ineta.
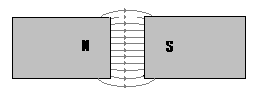
Para entender mejor el significado de la ecuación anterior es útil aplicarla al ejemplo en que un núcleo de hierro u otro material ferromagnético, tiene un bobinado de alambre de N vueltas en torno a una columna del núcleo como se muestra en la figura 1.
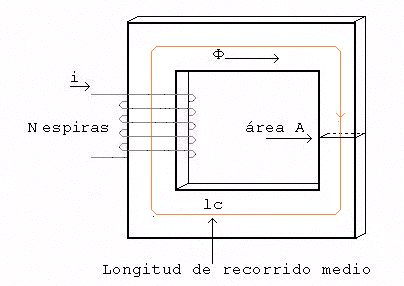
Núcleo magnético sencillo.
Por lo tanto todo el campo magnético producido por la corriente permanecerá esencialmente dentro del núcleo, de tal modo que el recorrido de integración de la ley de Ampere será lc. La corriente que pasa dentro del recorrido de integración Ineta es entonces, N * i, puesto que la bobina abraza el recorrido de integración N veces, mientras conduce la corriente i. La ley de amper se vuelve entonces
H * lc = N * i
Por consiguiente la magnitud de intensidad de campo magnético en el núcleo, debido a la corriente aplicada es
H = (N * i) / lc
b) Densidad de campo magnético (B):
La densidad de flujo magnético producido en un material está dada, por el producto de dos terminos. Su relación es la siguiente:
B = ð * H
Donde:
H: Intensidad de campo magnético: que representa el esfuerzo que ejerce la corriente para establecer un campo magnético. Su unidad es (Amper* vuelta) / metro (A*V/m)
ð : Permeabilidad magnética del material: que representa el esfuerzo que realiza la corriente para establecer un campo magnético en un material dado.Su unidad es Henrio/metro (H/m)
B: Densidad de flujo magnético. Su unidad es Weber/metro², Tessla (T)
c) Permeabilidad relativa (ð r):
Es la permeabilidad de cualquier otro material comparada con la permeabilidad del espacio libre.
ð r = ð ð ð 0
Donde: ðo: Permeabilidad del espacio libre
ð0 = 4ð ð ðððð
Para el núcleo de la figura la magnitud de la densidad de flujo es
B = ð * H = (ð * N * i) / lc
d) Flujo total (ð ):
El flujo total de un área dada se determina por
ð = ð B* dA
Donde: dA: Unidad de diferencia de área.
Por lo tanto si el vector de densidad de flujo es perpendicular a un plano de área A, y si la densidad de flujo es constante en toda el área, entonces, la ecuación se reduce a:
ð = B* A
Para el núcleo de la figura el flujo total debido a la corriente i en el bobinado es
ð = B * A = (ð * N * i * A) / lm
Donde A: Area de corte transversal del núcleo.
e) Enlace de flujo (ð ):
Es una forma de medir el magnetismo en una bobina, y su ecuación es
ð = N * ð
CIRCUITOS MAGNETICOS
Se entenderá por circuito magnético a una estructura ferromagnética acompañada de fuerzas magnetomotrices con la finalidad de canalizar líneas de fuerza magnéticas. Esta estructura puede contener espacios de aires atravesados por líneas de fuerza, estos espacios se conocen como entrehierros.
Es posible determinar un circuito magnético debido a que su comportamiento esta regido por ecuaciones análogas a aquellas de un circuito eléctrico.
El modelo de circuito magnético se usa a menudo en el diseño de maquinas eléctricas y transformadores para simplificar el, de otro modo, muy complejo proceso de diseño.
En un sencillo circuito eléctrico, como el ilustrado en la figura 2.a, la fuente de voltaje V, en causa una corriente I alrededor del circuito, a través de una resistencia R. La relación entre cantidades se obtiene mediante la ley de Ohm.
V = I* R
Analogías entre circuito eléctrico y circuito magnético:
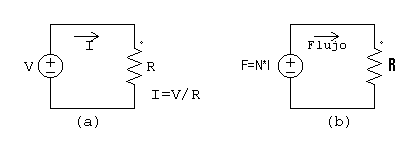
a) Un circuito electrico simple. b) El circuito magnético analogo a un núcleo de transformador.
-
En un circuito eléctrico, el voltaje o fuerza electromotriz es la que impulsa el flujo, en un circuito magnético se llama fuerza magnetomotriz (f.m.m), y se expresa por la siguiente ecuación
F = N * i
Donde:
F: Fuerza magnetomotriz, y su unidad es amper por vuelta (a*V).
N: Numero de vueltas del bobinado.
I: Corriente aplicada, su unidad es el Ampere.
-
En un circuito eléctrico, el voltaje aplicado causa el flujo de una corriente I. De modo semejante, en un circuito magnético la fuerza magnetomotriz aplicada causa la producción de un flujo magnético ð . La relación entre voltaje y corriente en un circuito eléctrico es la ley de ohm (V= I* R); de manera semejante, la relación entre fuerza magnetomotriz y flujo es:
F = ð ð ð
Donde
ð : Flujo magnético en weber.
ð : Reluctancia del circuito.
-
La reluctancia en un circuito magnético es la contraparte de la resistencia eléctrica y su unidad es amper-vuelta por weber (A*vuelta / weber)
-
Así como en un circuito eléctrico la conductancia es la reciproca de la resistencia, en un circuito magnético la permanencia es la reciproca de su reluctancia.
ρ = 1 / ð
ð = F * ρ
Bajo ciertas circunstancias es más fácil trabajar con la permanencia de un circuito magnético que con su reluctancia.
-
La reluctancias en un circuito magnético obedecen las mismas reglas a que obedecen en un circuito eléctrico.
La reluctancia equivalente en un circuito serie es :
Req = R1+ R2+ R3+.......
La reluctancia en un circuito paralelo es:
1/ Req = (1/ R1)+ (1/ R2)+ (1/ R3)+.........
La permanencia en un circuito serie o paralelo obedecen las mismas reglas que las conductancias eléctricas.
Precisión de los circuitos magnéticos
Los cálculos de flujo en el núcleo utilizando los conceptos de circuitos magnéticos, siempre son aproximados; a lo sumo tienen una precisión cercana a un 5% de la respuesta real. Hay una serie de razones para esta inexactitud inherente:
El concepto de circuito magnético supone que todo el flujo esta confinado dentro del núcleo magnético, esto no es totalmente cierto. La permeabilidad de un núcleo ferromagnético es de 2000 a 60000 veces la del aire, pero una pequeña fracción del flujo escapa hacia el poco permeable aire circundante. Este flujo fuera del núcleo se llama flujo de dispersión y cumple un papel importante en el diseño de la maquina eléctrica.
El calculo de la reluctancia supone cierta longitud de trayecto medio y un área de la sección transversal del núcleo. Estos supuestos no son totalmente acertados, especialmente en las esquinas.
En los materiales ferromagnéticos, la permeabilidad varia con la cantidad del flujo ya contenido en el material. Ello agrega todavía otra fuente de error al análisis de circuitos magnéticos, puesto que las reluctancias usadas en los cálculos de los circuitos magnéticosdependen de la permeabilidad del material.
Si hay entrehierros de aire en el recorrido del flujo en el núcleo, el área efectiva del corte transversal del entrehierro de airé será mayor que el área del corte transversal del núcleo de hierro en ambos lados (ver siguiente figura 3).
Efecto de borde de un campo magnético en un entrehierro. Nótese el incremento del área efectiva en el entrehierro, comparada con el área de la sección transversal del metal.
Parcialmente es posible corregir estas fuentes de error utilizando una longitud de trayecto medio o efectivo y el área del corte transversal en lugar de la longitud física o del área real, en los cálculos.
Hay muchas limitaciones inherentes al concepto de un circuito magnético, pero ello es todavía, la mejor herramienta disponible para calcular los flujos en el diseño de maquinas practicas. Los cálculos exactos, usando las ecuaciones de Maxwell, son muy difíciles y en todo caso muy poco necesarios, puesto que es preferible obtener resultados satisfactorios con el método aproximado.
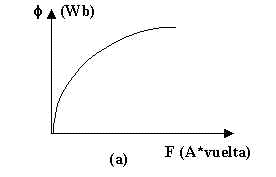
CURVAS DE MAGNETIZACION
La curva de magnetización de un material ferromagnetico es aquella que representa el magnetismo en el material como función de la fuerza magnetizante.
| Magnetismo | Fuerza magnetizante |
| ð | N * i |
| ð | i |
| B | H |
Estas curvas se obtienes debido a que la permeabilidad de los materiales ferromagnéticos no es constante, entonces, para ilustrar el comportamiento de la permeabilidad de un material ferromagnético se aplica una corriente continua al núcleo que se ilustra en la figura 1, iniciando con 0 A y subiéndola lentamente hasta la máxima corriente permitida. Cuando el flujo producido en el núcleo se pone en contra de la fuerza magnetomotriz que lo produce, el plano resultante luce como la figura 4a. Este tipo gráfico se llama curva de saturación o curva de magnetización.
|
|
|
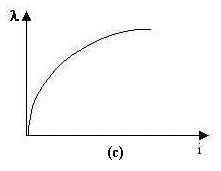
a) Esquema de una curva de magnetización de cc para un núcleo ferromagnético, expresada en terminos de flujo magnético (f) y fuerza magnetomotriz (F). b) Curva de magnetización expresada en terminos de densidad de flujo e intensidad de magnetización. c) Curva de magnetización expresada en terminos de enlace de flujo (l ) e intensidad de corriente.
Interpretación de la pendiente de la curva de magnetización:
Las tres curvas de magnetización anteriores son proporcionales (B - H ; ð - F; ð - i) y sus pendientes tienen la siguiente interpretación.
-
Curva de magnetización ð v/s i:
La pendiente de esta curva corresponde a la inductancia de la bobina
L = ð / i
-
Curva de magnetización B v/s H:
La pendiente de esta curva corresponde a la permeabilidad magnética del material
ð = B / H
-
Curva de magnetización ð v/s N * i
La pendiente de esta curva corresponde a la permanencia magnética del material.
ρ = ð / (N * i)
MAGNETISMO EN CORRIENTE ALTERNA
Cuando un conductor, como por ejemplo un cable metálico, se mueve a través del espacio libre entre los dos polos de un imán, los electrones del cable, con carga negativa, experimentan una fuerza a lo largo de él y se acumulan en uno de sus extremos, dejando en el otro extremo núcleos atómicos con carga positiva, parcialmente despojados de electrones. Esto crea una diferencia de potencial, o voltaje, entre los dos extremos del cable; si estos extremos se conectan con un conductor, fluirá una corriente alrededor del circuito. Éste es el principio que da base a los generadores eléctricos rotatorios, en los que un bucle de hilo conductor gira dentro de un campo magnético para producir un voltaje y generar una corriente en un circuito cerrado.
La inducción ocurre solamente cuando el conductor se mueve en ángulo recto con respecto a la dirección del campo magnético. Este movimiento es necesario para que se produzca la inducción, pero es un movimiento relativo entre el conductor y el campo magnético. De esta forma, un campo magnético en expansión y compresión puede crearse con una corriente a través de un cable o un electroimán. Dado que la corriente del electroimán aumenta y se reduce, su campo magnético se expande y se comprime (las líneas de fuerza se mueven hacia adelante y hacia atrás). El campo en movimiento puede inducir una corriente en un hilo fijo cercano.
LEY DE FARADAY.
VOLTAJE INDUCIDO POR UN CAMPO MAGNÉTICO
La ley de Faraday y es la base de la manera de operar los transformadores.
Faraday fue el primer científico experimental de su época que realizó estudios en los campos de la electricidad y el magnetismo. En 1821 trazó el campo magnético alrededor de un conductor por el que circula una corriente eléctrica (la existencia del campo magnético había sido observada por vez primera por el físico danés Hans Christian Oersted en 1819). En 1831 Faraday descubrió la inducción electromagnética, y el mismo año demostró la inducción de una corriente eléctrica por otra.
La ley de Faraday establece que si un flujo pasa por una vuelta de una bobina de alambre, se inducirá un voltaje en la vuelta de alambre, proporcional a la tasa de cambio en el flujo con relación al tiempo. En forma de ecuación,
eind = -dð / dt
en donde eind es el voltaje inducido en la vuelta de la bobina y ð es el flujo que pasa por la vuelta. Si una bobina tiene N número de vueltas y el mismo flujo pasa por todas ellas, entonces el voltaje inducido a través de toda la bobina se expresa por:
eind = -N dð / dt
en donde:
eind = voltaje inducido en la bobina
N = número de vueltas en la bobina de alambre
ð = flujo que pasa a través de la bobina
El signo menos de la ecuación es una expresión de la ley de Lenz. Esta establece que la dirección del voltaje inducido en la bobina es tal que si sus extremos se pusieran en corto circuito, produciría una corriente que causaría un flujo para oponerse al cambio de flujo original. Puesto que el voltaje inducido se opone al cambio que lo causa, se incluye un signo menos en la ecuación .
VOLTAJE INDUCIDO SOBRE UN CONDUCTOR MÓVIL EN UN CAMPO MAGNÉTICO
Hay una tercera forma principal en la cual un campo magnético interactúa con sus alrededores. Si un alambre con una orientación apropiada se mueve a través de un campo magnético, se obtiene la inducción de un voltaje en dicho alambre. El voltaje inducido en el alambre se expresa por:
eind = (v x B) • 1
en donde
v = velocidad del alambre.
B = densidad de flujo magnético.
1 = longitud del conductor en el campo magnético.
El vector 1 señala a lo largo de la dirección del alambre hacia el extremo que se supone positivo. Cuál de los dos extremos se supone positivo es completamente arbitrario. Si la suposición inicial resulta equivocada, entonces el valor del voltaje calculado resultante será negativo e indicará equivocada la selección de referencia.
El voltaje en el conductor se formará de tal manera que el extremo positivo está en la dirección del vector v x B.
Tipos de materiales magnéticos
Las propiedades magnéticas de los materiales se clasifican siguiendo distintos criterios.
Una de las clasificaciones de los materiales magnéticos —que los divide en diamagnéticos, paramagnéticos y ferromagnéticos— se basa en la reacción del material ante un campo magnético.
Cuando se coloca un material diamagnético en un campo magnético, se induce en él un momento magnético de sentido opuesto al campo. En la actualidad se sabe que esta propiedad se debe a las corrientes eléctricas inducidas en los átomos y moléculas individuales. Estas corrientes producen momentos magnéticos opuestos al campo aplicado. Muchos materiales son diamagnéticos; los que presentan un diamagnetismo más intenso son el bismuto metálico y las moléculas orgánicas que, como el benceno, tienen una estructura cíclica que permite que las corrientes eléctricas se establezcan con facilidad.
El comportamiento paramagnético se produce cuando el campo magnético aplicado alinea todos los momentos magnéticos ya existentes en los átomos o moléculas individuales que componen el material. Esto produce un momento magnético global que se suma al campo magnético. Los materiales paramagnéticos suelen contener elementos de transición o lantánidos con electrones desapareados.
El paramagnetismo en sustancias no metálicas suele caracterizarse por una dependencia de la temperatura: la intensidad del momento magnético inducido varía inversamente con la temperatura. Esto se debe a que al ir aumentando la temperatura, cada vez resulta más difícil alinear los momentos magnéticos de los átomos individuales en la dirección del campo magnético.
Las sustancias ferromagnéticas son las que, como el hierro, mantienen un momento magnético incluso cuando el campo magnético externo se hace nulo. Este efecto se debe a una fuerte interacción entre los momentos magnéticos de los átomos o electrones individuales de la sustancia magnética, que los hace alinearse de forma paralela entre sí. En circunstancias normales, los materiales ferromagnéticos están divididos en regiones llamadas `dominios'; en cada dominio, los momentos magnéticos atómicos están alineados en paralelo. Los momentos de dominios diferentes no apuntan necesariamente en la misma dirección.
Aunque un trozo de hierro normal puede no tener un momento magnético total, puede inducirse su magnetización colocándolo en un campo magnético, que alinea los momentos de todos los dominios. La energía empleada en la reorientación de los dominios desde el estado magnetizado hasta el estado desmagnetizado se manifiesta en un desfase de la respuesta al campo magnético aplicado, conocido como `histéresis'.
Un material ferromagnético acaba perdiendo sus propiedades magnéticas cuando se calienta. Esta pérdida es completa por encima de una temperatura conocida como punto de Curie, llamada así en honor del físico francés Pierre Curie, que descubrió el fenómeno en 1895. (El punto de Curie del hierro metálico es de unos 770 °C).
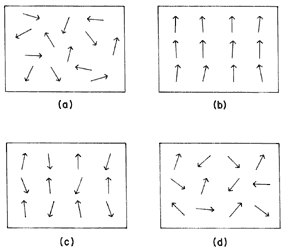
Diferentes tipos de materiales magnéticos.
a) Paramagneto. Los espines apuntan en direcciónes al azar, las cuales varían al paso del tiempo.
b) Ferromagnetos. Los espines tienen tendencia a alinearse en una misma dirección.
c) antiferromagnetos. Tendencia de los espines a alinearse antiparalelamente a sus vecinos.
d) Vidrios de espín. Los espines apuntan en direcciones aparentemente al azar, pero fijas al paso del tiempo. Para poder diferenciar entre los casos a) y b) necesitamos observar ambos sistemas durante un largo tiempo.
Propiedades de los materiales magnéticos
-
Densidad de Flujo y Permeabilidad.
El número de líneas ![]()
N dibujadas a través de la unidad de área ![]()
A es directamente proporcional a la intensidad del campo eléctrico E.
![]()
La constante de proporcionalidad ![]()
, que determina el número de líneas dibujadas, es la permisividad del medio por el cual pasan las líneas.
Puede presentarse una descripción semejante para un campo magnético si se considera el flujo magnético ![]()
que pasa perpendicularmente a través de una unidad de área A. Esta razón B se llama densidad de flujo magnético.
" La densidad de flujo magnético en una región de un campo magnético es el número de líneas de flujo que atraviesan perpendicularmente la unidad de área en dicha región ".
![]()
En él SI la unidad de flujo magnético es el weber (Wb). Por tanto, la unidad de densidad de flujo será webers por metro cuadrado, y se redefine como el tesla (T). Una unidad antigua que aún se usa es el gauss (G). En resumen,
![]()
Ejemplo 5.4. Cálculo del flujo magnético en una espira rectangular.
Una espira rectangular de 19cm de ancho y 20cm de largo forma un ángulo de 30° con respecto al flujo magnético. Si la densidad de flujo es 0.3 T, calcúlese el flujo magnético que penetra en la espira.
Solución
El área efectiva que el flujo penetra es aquella componente del área perpendicular al flujo. Así pues, de la ecuación
![]()

La densidad de flujo en cualquier punto de un campo magnético se ve muy afectada por la naturaleza del medio o por la naturaleza de algún material que se coloque entre el polo y el objeto. Por esta razón conviene definir un nuevo vector de campo magnético, la intensidad del campo magnético H, que no depende de la naturaleza del medio. En cualquier caso, el número de líneas establecidas por unidad de área es directamente proporcional a la intensidad del campo magnético H. Puede escribirse
![]()
donde la constante de proporcionalidad µ es la permeabilidad del medio a través del cual pasan las líneas de flujo. La ecuación anterior es análoga a la ecuación para campos eléctricos.
Así pues, la permeabilidad de un medio puede definirse como la medida de la capacidad para establecer líneas de flujo magnético. Cuanto más grande sea la permeabilidad del medio, mayor será el número de líneas de flujo que pasarán por la unidad de área.
La permeabilidad del espacio libre (el vacío) se denota mediante µ0.
Los materiales magnéticos se clasifican conforme a sus permeabilidades comparadas con la del espacio vacío. La razón de la permeabilidad de un material con la correspondiente para el vacío se llama permeabilidad relativa y está expresada por
![]()
Materiales con una permeabilidad relativa ligeramente menor que la unidad tienen la propiedad de poder ser repelidos débilmente por un imán potente. Este tipo de materiales se denominan diamagnéticos y la propiedad correspondiente, diamagnetismo.
Por otro lado, a los materiales que presentan una permeabilidad ligeramente mayor que la del vacío se denominan paramagnéticos. Dichos materiales son atraídos débilmente por un imán poderoso.
Pocos materiales, como el hierro, cobalto, níquel, acero y aleaciones de estos elementos prestan permeabilidades extremadamente altas, comprendidas desde pocos cientos a miles de veces la del vacío. Estos materiales son atraídos fuertemente por un imán y se dice que son ferromagnéticos.
MATERIALES FERROMAGNETICOS
Los materiales ferromagnéticos, compuestos de hierro y sus aleaciones con cobalto, tungsteno, níquel, aluminio y otros metales, son los materiales magnéticos más comunes y se utilizan para el diseño y constitución de núcleos de los transformadores y maquinas eléctricas. En un transformador se usan para maximizar el acoplamiento entre los devanados, así como para disminuir la corriente de excitación necesaria para la operación del transformador. En las maquinas eléctricas se usan los materiales ferromagnéticos para dar forma a los campos, de modo que se logren hacer máximas las características de producción de par.
Estos materiales han evolucionado mucho con el paso del tiempo lo que implica mas eficiencia, reducción de volúmenes y costo, en el diseño de transformadores y maquinas eléctricas.
Los materiales ferromagnéticos poseen las siguientes propiedades y características que se detallan a continuación.
Propiedades de los materiales ferromagneticos.
-
Aparece una gran inducción magnética al aplicarle un campo magnético.
-
Permiten concentrar con facilidad líneas de campo magnético, acumulando densidad de flujo magnético elevado.
-
Se utilizan estos materiales para delimitar y dirigir a los campos magnéticos en trayectorias bien definidas.
-
Permite que las maquinas eléctricas tengan volúmenes razonables y costos menos excesivos.
Características de los materiales ferromágneticos.
Los materiales ferromágneticos se caracterizan por uno o varios de los siguientes atributos:
-
Pueden imanarse mucho más fácilmente que los demás materiales. Esta característica viene indicada por una gran permeabilidad relativa ð /ð r.
-
Tienen una inducción magnética intrínseca máxima Bmax muy elevada.
-
Se imanan con una facilidad muy diferente según sea el valor del campo magnético. Este atributo lleva una relación no lineal entre los módulos de inducción magnética(B) y campo magnético.
-
Un aumento del campo magnético les origina una variación de flujo diferente de la variación que originaria una disminución igual de campo magnético. Este atributo indica que las relaciones que expresan la inducción magnética y la permeabilidad (ð ) como funciones del campo magnético, no son lineales ni uniformes.
-
Conservan la imanación cuando se suprime el campo.
-
Tienden a oponerse a la inversión del sentido de la imanación una vez imanados.
Materiales ferromagnéticos para transformadores:
La aleación ferromagnética más utilizada para el diseño de núcleos de transformadores es la aleación hierro-silicio, esta aleación es la producida en mayor cantidad y esta compuesta por hierro esencialmente puro con 1-6% de silicio, dependiendo este porcentaje del fin a que se destine el material. Dando a esta aleación un tratamiento térmico adecuado, se obtiene un material que comparado con el hierro, tiene mejores propiedades magnéticas para campos magnéticos débiles, una resistividad mayor y sufren perdidas totales menores en el núcleo. Esta aleación se lamina en chapas y flejes, principalmente de espesores comprendidos entre 0,35 y 0,635 mm recocidos; en el lenguaje corriente se le conoce con el nombre de acero al silicio o Chapa magnética.
Las chapas de mejor calidad presentan mayor contenido en silicio, entre el 4 y el 5. El silicio eleva la dureza del material, por lo que su porcentaje se determina según el empleo al que se designa la chapa. Para maquinas rotatorias el limite superior es aproximadamente del 4%, teniendo en cuenta el peligro de la fragilidad. También se prefieren chapas de menor contenido de silicio cuando las densidades de funcionamiento son elevadas o cuando se desea una elevada conductividad calorífica. Las perdidas en el núcleo y el coeficiente de envejecimiento aumentan al disminuir el contenido de silicio.
La fabricación de la chapa magnética ha llegado a estar normalizada en considerable extensión por lo que los datos magnéticos publicados por diversos fabricantes no se diferencian, calidad por calidad, excesivamente.
El transformador
Dispositivo eléctrico que consta de una bobina de cable situada junto a una o varias bobinas más, y que se utiliza para unir dos o más circuitos de corriente alterna (CA) aprovechando el efecto de inducción entre las bobinas. La bobina conectada a la fuente de energía se llama bobina primaria. Las demás bobinas reciben el nombre de bobinas secundarias. Un transformador cuyo voltaje secundario sea superior al primario se llama transformador elevador. Si el voltaje secundario es inferior al primario este dispositivo recibe el nombre de transformador reductor. El producto de intensidad de corriente por voltaje es constante en cada juego de bobinas, de forma que en un transformador elevador el aumento de voltaje de la bobina secundaria viene acompañado por la correspondiente disminución de corriente.
La característica práctica más importante de la corriente alterna es que su voltaje puede cambiarse mediante un sencillo dispositivo electromagnético denominado transformador. Cuando una corriente alterna pasa por una bobina de alambre, el campo magnético alrededor de la bobina se intensifica, se anula, se vuelve a intensificar con sentido opuesto y se vuelve a anular.
Si se sitúa otra bobina en el campo magnético de la primera bobina, sin estar directamente conectada a ella, el movimiento del campo magnético induce una corriente alterna en la segunda bobina. Si esta segunda bobina tiene un número de espiras mayor que la primera, la tensión inducida en ella será mayor que la tensión de la primera, ya que el campo actúa sobre un número mayor de conductores individuales. Al contrario, si el número de espiras de la segunda bobina es menor, la tensión será más baja que la de la primera.
Teoría del funcionamiento de un transformador
Cuando se conecta el primario a una fuente de fem alterna, por el bobinado comienza a pasar una corriente alterna.
En cuanto fluye una corriente por un conductor se crea un campo magnético alrededor de él. Si la corriente cambia continuamente en magnitud y polaridad, el campo magnético que se origina en el núcleo de hierro hará lo mismo.
El campo magnético alterno está, por tanto, continuamente expandiéndose y contrayéndose. Como el circuito magnético es cerrado. La variación del campo magnético es la misma en cualquier parte del núcleo.
Las líneas magnéticas al expandirse y contraerse cortarán a los conductores situados en cualquier parte del núcleo, y de acuerdo con el experimento de Faraday, en éstos aparecerá una fem inducida.
Como a cada conductor sobre el núcleo le corta el mismo flujo. La fem inducida por vuelta será la misma. Por tanto, el voltaje en cada bobinado será proporcional al número de vueltas.
El transformador
Sección transversal de un transformador Esquema muy simplificado de un transformador de los denominados monofásicos.
En la parte izquierda de la figura se puede ver la bobina o arrollamiento primario, y en la derecha el secundario.
En el caso que se muestra, el transformador está funcionando sin carga, esto es, sin ningún dispositivo consumidor de electricidad conectado al secundario.
En esas condiciones, la proporción entre los voltajes o tensiones U corresponde a la proporción entre los números de espiras N, cumpliéndose la relación U1/U2 = N1/N2.
Aplicación de los transformadores
En el campo de la electrónica se suelen utilizar con más frecuencia transformadores con capacidades de alrededor de 1 kilovatio antes de los rectificadores, que a su vez proporcionan corriente continua (CC) al equipo. Estos transformadores electrónicos de energía se fabrican normalmente con bloques de láminas de aleación de acero, llamadas laminaciones, alrededor de las cuales se instalan las bobinas de hilo de cobre. Los transformadores a niveles de entre 1 y 100 vatios se usan principalmente como transformadores reductores, para acoplar circuitos electrónicos a los altavoces de equipos de radio, televisión y alta fidelidad. Conocidos como transformadores de audio, estos dispositivos utilizan sólo una pequeña fracción de su potencia nominal para la producción de señales en las frecuencias audibles, con un nivel de distorsión mínimo. Los transformadores se valoran según su capacidad de reproducción de frecuencias de ondas audibles (entre 20 Hz y 25 KHz) con distorsiones mínimas a lo largo de todo el espectro de sonido.
A niveles de potencia por debajo de un milivatio, los transformadores se utilizan sobre todo para acoplar frecuencias extremadamente elevadas (UHF), frecuencias muy altas (VHF), frecuencias de radio (RF) y frecuencias intermedias (IF), así como para aumentar su voltaje. Estos transformadores de alta frecuencia operan por lo general en circuitos sintonizados o resonantes, en los que se utiliza la sintonización para eliminar ruidos eléctricos no deseados cuyas frecuencias se encuentran fuera del rango de transmisión deseado.
Aplicación de los transformadores en la transmisión de energía eléctrica
La generación y transporte de energía en forma de electricidad tiene importantes ventajas económicas debido al coste por unidad generada. Las instalaciones eléctricas también permiten utilizar la energía hidroeléctrica a mucha distancia del lugar donde se genera. Estas instalaciones suelen utilizar corriente alterna, ya que es fácil reducir o elevar el voltaje con transformadores. De esta manera, cada parte del sistema puede funcionar con el voltaje apropiado. Las instalaciones eléctricas tienen seis elementos principales: la central eléctrica, los transformadores, que elevan el voltaje de la energía eléctrica generada a las altas tensiones utilizadas en las líneas de transporte, las líneas de transporte, las subestaciones donde la señal baja su voltaje para adecuarse a las líneas de distribución, las líneas de distribución y los transformadores que bajan el voltaje al valor utilizado por los consumidores.
En una instalación normal, los generadores de la central eléctrica suministran voltajes de 26.000 voltios; voltajes superiores no son adecuados por las dificultades que presenta su aislamiento y por el riesgo de cortocircuitos y sus consecuencias. Este voltaje se eleva mediante transformadores a tensiones entre 138.000 y 765.000 voltios para la línea de transporte primaria (cuanto más alta es la tensión en la línea, menor es la corriente y menores son las pérdidas, ya que éstas son proporcionales al cuadrado de la intensidad de corriente). En la subestación, el voltaje se transforma en tensiones entre 69.000 y 138.000 voltios para que sea posible transferir la electricidad al sistema de distribución. La tensión se baja de nuevo con transformadores en cada punto de distribución. La industria pesada suele trabajar a 33.000 voltios (33 kilovoltios), y los trenes eléctricos requieren de 15 a 25 kilovoltios. Para su suministro a los consumidores se baja más la tensión: la industria suele trabajar a tensiones entre 380 y 415 voltios, y las viviendas reciben entre 220 y 240 voltios en algunos países y entre 110 y 125 en otros.
El desarrollo actual de los rectificadores de estado sólido para alta tensión hace posible una conversión económica de alta tensión de corriente alterna a alta tensión de corriente continua para la distribución de electricidad.
Esto evita las pérdidas inductivas y capacitivas que se producen en la transmisión de corriente alterna.
Cualquier sistema de distribución de electricidad requiere una serie de equipos suplementarios para proteger los generadores, transformadores y las propias líneas de conducción. Suelen incluir dispositivos diseñados para regular la tensión que se proporciona a los usuarios y corregir el factor de potencia del sistema.
Los Transformadores de Potencia son grandes dispositivos usados en los sistemas de generación y transporte de electricidad y en pequeñas unidades electrónicas.
Los transformadores de potencia industriales y domésticos, que operan a la frecuencia de la red eléctrica, pueden ser monofásicos o trifásicos y están diseñados para trabajar con voltajes y corrientes elevados.
Para que el transporte de energía resulte rentable es necesario que en la planta productora de electricidad un transformador eleve los voltajes, reduciendo con ello la intensidad. Las pérdidas ocasionadas por la línea de alta tensión son proporcionales al cuadrado de la intensidad de corriente por la resistencia del conductor. Por tanto, para la transmisión de energía eléctrica a larga distancia se utilizan voltajes elevados con intensidades de corriente reducidas.
En el extremo receptor los transformadores reductores reducen el voltaje, aumentando la intensidad, y adaptan la corriente a los niveles requeridos por las industrias y las viviendas, normalmente alrededor de los 240 voltios.
Los transformadores de potencia deben ser muy eficientes y deben disipar la menor cantidad posible de energía en forma de calor durante el proceso de transformación. Las tasas de eficacia se encuentran normalmente por encima del 99% y se obtienen utilizando aleaciones especiales de acero para acoplar los campos magnéticos inducidos entre las bobinas primaria y secundaria. Una disipación de tan sólo un 0,5% de la potencia de un gran transformador genera enormes cantidades de calor, lo que hace necesario el uso de dispositivos de refrigeración.
TRANSFORMADOR DE POTENCIA
|
| Descripción: |
TRANSFORMADOR DE DISTRIBUCION
Se denomina transformadores de distribución, generalmente los transformadores de potencias iguales o inferiores a 500 kVA y de tensiones iguales o inferiores a 67 000 V, tanto monofásicos como trifásicos. Aunque la mayoría de tales unidades están proyectadas para montaje sobre postes, algunos de los tamaños de potencia superiores, por encima de las clases de 18 kV, se construyen para montaje en estaciones o en plataformas. Las aplicaciones típicas son para alimentar a granjas, residencias, edificios o almacenes públicos, talleres y centros comerciales.
A continuación se detallan algunos tipos de transformadores de distribución.
Transformadores Secos Encapsulados en Resina Epoxi
|
| Descripción: Características Generales: |
Transformadores Herméticos de Llenado Integral
|
|
|
Transformadores Rurales
|
|
|
Transformadores Subterráneos
|
| Transformador de construcción adecuada para ser instalado en cámaras, en cualquier nivel, pudiendo ser utilizado donde haya posibilidad de inmersión de cualquier naturaleza. Potencia: 150 a 2000KVA Alta Tensión: 15 o 24,2KV Baja Tensión: 216,5/125;220/127;380/220;400/231V |
TRANSFORMADOR DE CORRIENTE TT/CC
|
| Los transformadores de corriente se utilizan para tomar muestras de corriente de la línea y reducirla a un nivel seguro y medible, para las gamas normalizadas de instrumentos, aparatos de medida, u otros dispositivos de medida y control. Ciertos tipos de transformadores de corriente protegen a los instrumentos al ocurrir cortocircuitos. Los valores de los transformadores de corriente son: Carga nominal: 2.5 a 200 VA, dependiendo su función. Corriente nominal: 5 y 1A en su lado secundario. se definen como relaciones de corriente primaria a corriente secundaria. Unas relaciones típicas de un transformador de corriente podrían ser: 600/5, 800/5, 1000/5. Usualmente estos dispositivos vienen con un amperímetro adecuado con la razón de transformación de los transformadores de corriente, por ejemplo: un transformador de 600/5 está disponible con un amperímetro graduado de 0 - 600A. |
TRANSFORMADOR DE POTENCIAL TT/PP
|
| Es un transformador devanado especialmente, con un primario de alto voltaje y un secundario de baja tensión. Tiene una potencia nominal muy baja y su único objetivo es suministrar una muestra de voltaje del sistema de potencia, para que se mida con instrumentos incorporados. Además, puesto que el objetivo principal es el muestreo de voltaje deberá ser particularmente preciso como para no distorsionar los valores verdaderos. Se pueden conseguir transformadores de potencial de varios niveles de precisión, dependiendo de que tan precisas deban ser sus lecturas, para cada aplicación especial. |
Tipos de transformadores
Autotransformador:
Los autotransformadores se usan normalmente para conectar dos sistemas de transmisión de tensiones diferentes, frecuentemente con un devanado terciario en triángulo. De manera parecida, los autotransformadores son adecuados como transformadores elevadores de centrales cuando sé desea alimentar dos sistemas de transporte diferentes. En este caso el devanado terciario en triángulo es un devanado de plena capacidad conectado al generador y los dos sistemas de transporte se conectan al devanado, autotransformador. El autotransformador no sólo presenta menores pérdidas que el transformador normal, sino que su menor tamaño y peso permiten el transporte de potencias superiores.
Transformador Trifásico:
Casi todos los sistemas importantes de generación y distribución de potencia del mundo son, hoy en día, sistemas de ca trifásicos. Puesto que los sistemas trifásicos desempeñan un papel tan importante en la vida moderna, es necesario entender la forma como los transformadores se utilizan en ella.
|
|
|
Los transformadores para circuitos trifásicos pueden construirse de dos maneras. Estas son:
- Tomando tres transformadores monofásicos y conectándolos en un grupo trifásico.
- Haciendo un transformador trifásico que consiste en tres juegos de devanados enrollados sobre un núcleo común.
Para el análisis de su circuito equivalente, hay que representar cada uno de los transformadores monofásicos que componen un banco trifásico por un circuito equivalente. Como los efectos de las capacidades de los devanados y de los armónicos de las corrientes de excitación suelen ser despreciables, podrá utilizarse cualquiera de los circuitos equivalentes deducidos para el caso de los monofásicos; los más útiles para el presente estudio son los de la figura 1.

.Circuitos equivalentes para un transformador sólo
En ellos, el transformador esta representado, como en el teorema de Thévenin, por su impedancia en cortocircuito en serie con su tensión en circuito abierto; la razón de las tensiones en circuito abierto está representada por un transformador ideal; y las características de excitación están representadas por la admitancia en circuito abierto.
Los valores de los parámetros pueden obtenerse a partir de los datos de diseño o ensayos en circuito abierto o en cortocircuito tomados a uno u otro lado del transformador, y estos valores se pueden emplear, sin modificación, o en el circuito equivalente de la figura 1a (en el cual se coloca la admitancia de excitación en el lado primario) o en el circuito equivalente de la figura 1b (en el cual se coloca la admitancia de excitación en el lado del secundario) En muchos problemas, los efectos de la corriente de excitación son tan pequeños que puede despreciarse por completo la corriente de excitación y representarse el transformador por su impedancia equivalente en serie con un transformador ideal. Si se quiere, las impedancias equivalentes y admitancias de excitación de la figura 1 se puede referir al otro lado del transformador multiplicando o dividiendo, según sea el caso, por el cuadrado de la razón de transformación.
El circuito equivalente de un banco trifásico de transformadores puede trazarse conectando los circuitos equivalentes de las unidades de acuerdo con las conexiones del banco. Por ejemplo, en la figura 2a puede verse el circuito equivalente de un banco estrella-estrella y en la figura 2b un circuito equivalente de un banco triángulo. En la figura 2, las Y representan las admitancias en circuito abierto o de excitación y las Z las impedancias en cortocircuitos o equivalentes.

Circuitos equivalentes trifásicos; a) Conexión estrella-estrella, y b) Conexión triángulo-triángulo.
En el análisis de sistemas de potencia es frecuentemente necesario combinar las impedancias de los transformadores con las impedancias de las líneas de transmisión a las que están conectados. Luego, resulta a menudo conveniente representar un grupo de devanados conectados en triángulo por un circuito equivalente conectado en estrella, ya que en la conexión en estrella las impedancias equivalentes que representan a los transformadores están en serie con los tres terminales de línea y por lo tanto pueden sumarse directamente a las impedancias de fase de los circuitos de transmisión. Ya se sabe que, visto desde sus tres terminales, un triángulo de elementos de circuito puede sustituirse por una estrella equivalente. Así, las admitancias de excitación YAB , YBC , YCA conectadas en triángulo de la figura 2b son equivalentes a las admitancias YA , YB , YC conectadas en estrella cuyos valores vienen dados por las conocidas relaciones.
YA = (YAB YBC + YBC YCA + YBC YCA ) / YBC
YB = (YAB YBC + YBC YCA + YBC YCA ) / YCA
YC = (YAB YBC + YBC YCA + YBC YCA ) / YAB
Además, las impedancias Zab , Zbc , Zca de la figura 2b que forman parte de un sistema conectado en triángulo, pueden sustituirse por impedancias conectadas en estrella. Así, el teorema de Thévenin, el banco triángulo-triángulo de la figura 2b es equivalente en su lado de secundarios a un generador conectado en estrella que cree las mismas tensiones de secundario entre línea y línea en circuito abierto y conectado en serie con impedancias cuyos valores sean las equivalentes en estrella de las impedancias en cortocircuito de los transformadores medidas desde los terminales de sus secundarios. Luego, los transformadores ideales conectados en triángulo-triángulo de la figura 2b pueden sustituirse por un banco estrella-estrella que dé las mismas tensiones en circuito abierto, y las impedancias en cortocircuito de los transformadores pueden representarse por impedancias en estrella conectadas en serie con cada terminal de línea. Las relaciones entre las impedancias en cortocircuito Za , Zb , Zc vienen dadas por las conocidas relaciones,
Za = (Zab Zca) / (Zab + Zbc + Zca)
Zb = (Zab Zbc) / (Zab + Zbc + Zca)
Zc = (Zbc Zca) / (Zab + Zbc + Zca)
Por tanto, por lo que concierne a sus efectos sobre los circuitos exteriores, un grupo de devanados conectados en triángulo puede representarse por un circuito equivalente conectado en estrella, como en la figura 2a, con tal que los parámetros de la estrella equivalente estén relacionados con los parámetros reales de los transformadores conectados en triángulo en la forma indicada por las ecuaciones anteriores y con tal que las tensiones en circuito abierto entre línea y línea del circuito equivalente conectado en estrella sean las mismas que las de los devanados conectados en triángulo. Es decir, en el caso de un banco triángulo-triángulo los transformadores ideales pueden sustituirse por un banco estrella-estrella que dé las mismas tensiones de funcionamiento. Análogamente, a menudo se representa un banco triángulo-estrella (o estrella-triánfgulo) por un circuito equivalente estrella-estrella, como en la figura 2a, que dé las mismas magnitudes de las tensiones en circuito abierto entre línea y línea. Sin embargo, a causa del desfasaje introducido por la conexión triángulo-estrella, el circuito equivalente estrella-estrella de un banco triángulo-estrella no presenta las relaciones correctas de fase entre las corrientes de primario y secundario o entre las tensiones de primario y secundario, aun cuando presente correctamente las relaciones entre las corrientes y tensiones de cada lado.
DIAGRAMA FASORIAL
Para obtener los diagramas vectoriales de un transformador trifásico tipo núcleo o asimétrico, hay que estudiar en forma detallada lo que sucede en un nucleolo tipo núcleo de tres ramas como el que se muestra en la siguiente figura 3.

Figura 3. Nucleo trifasico tipo nucleo de tres ramas
De la figura consideramos a las partes del núcleo comprendidas entre los puntos a-b, c-d y g-h como ramas pertenecientes a cada fase, o ramas del núcleo. Las zonas comprendidas entre a y g y entre b y h son las culatas, e influirán en forma distinta para cada rama. La reluctancia magnética de cada rama la indicamos con R, y suponemos qué son las tres iguales, lo que es cierto; la reluctancia de cada culata la llamarnos r, y hay dos iguales, la superior y la inferior. Los puntos de concurrencia de los tres flujos son: el c para la parte superior y el d para la parte inferior. Luego, las ff.mm.mm. comprendidas entre esos dos puntos, y correspondientes a cada una de las tres ramas, deben sumarse. Cada f.m.m. está dada por el producto del flujo y la reluctancia magnética, según sabemos, con lo que se tiene, considerando el orden de las ramas indicado en la figura:
Reluctancia rama 1: R + ½ r + ½ r = R + r
Reluctancia rama 2: R
Reluctancia rama 3: R + ½ r + ½ r = R + r
Que resultan distintas, pues la rama primera y tercera tienen mayor reluctancia magnética que la rama central o N° 2. Los tres flujos son iguales, pues el sistema de tensiones aplicado a las tres bobinas primarias está formado por tres tensiones iguales desfasadas 120º, luego, multiplicando el flujo por cada reluctancia tenemos:
F1 = ð1 (R + r) (1)
F2 = ð2 * R (2)
F3 = ð3 (R + r) (3)
En cada instante, como corresponde a un sistema trifásico normal, dos vectores tienen un sentido y el tercero tiene sentido contrario, es decir, que podernos suponer a la rama central con sentido contrario a las laterales. Hemos llamado a cada f.m.m: con la letra F, y con el subíndice qué corresponde a su rama y colocamos los mismos subíndices al flujo, para contemplar el hecho que, siendo alternados, tienen distintos valores instantáneos en magnitud y sentido. Si hacernos la suma de las ff.mm.mm. para la mitad izquierda del núcleo, para contemplar el efecto de la rama central sobre las laterales y viceversa, se tiene:
F1 - F2 = ð 1 (R + r) - ð 2 R (4)
Que se ha obtenido restando las ecuaciones (1) y (2), y que ha resultado una resta puesto que la segunda debe tener sentido contrario a la primera. Si hacemos lo mismo con las ecuaciones [3] y [4], se tiene:
F3 - F2 = ð 3 (R + r) - ð 2 R (5)
Ahora estamos en presencia de un par de ecuaciones, la [4] y la [5], que nos permitirán hacer algunas deducciones. El objeto de haberlas planteado, es para poder encontrar nuevas ecuaciones que dan las ff.mm.mm. en forma más conveniente para su interpretación.
Para disponer de otras ecuaciones que nos serán de utilidad, digamos que la suma de los valores de los tres flujos y las tres ff.mm.mm. debe ser constantemente nula, lo que ya sabemos, pero que escribimos así:
F1 + F2 + F3 = 0 (6)
ð1 + ð 2 + ð3 = 0 (7)
Y que nos permitirán reemplazar la suma de dos de estos valores por el tercero con signo cambiado, cuando nos sea necesario.
Para operar, restemos las dos ecuaciones (4) y (5), que nos dan:
F1 - F3 = ð1 (R + r) - ð3 (R + r) (8)
Y ahora sumamos esas mismas ecuaciones, con lo que se tiene:
F1 - F3 - 2F2 = ð1 (R + r) - ð3 (R + r) + ð2 R (9)
Y ahora analicemos si tenemos los elementos necesarios para encontrar el valor de cada f.m.m. Si cambiamos en la ecuación [9] la suma de las ff.mm.mm. 1 y 3 por- F2, de acuerdo con la [6], nos queda una ecuación en la cual sólo aparece esta última f.m.m., y que puede ser ordenada así:
-3 F2 = (R + r) (ð 1 - ð3) - 2 ð2 R
Pero por la [7], la suma de los dos flujos dentro del paréntesis puede ser cambiada por el flujo de la rama 2, con signo cambiado, y finalmente resulta:
F2 = ð2* R + (1/3) * ð2 r (10)
Ahora tenemos el valor de la f.m.m. de la rama 2, dado como suma vectorial de dos cantidades. Encontremos los valores de las otras dos ff.mm.mm. Para ello, reemplazamos la ecuación [10] en la [9] en lugar de F2, y disponemos de una ecuación que nos da la suma de las dos ff.mm.mm. La ecuación. [8] nos da la diferencia de esas mismas ff.mm.mm., de manera qué se puede obtener cada una de ellas por simple proceso algebraico. Sumando y dividiendo por 2, se tiene:
F1 = ð1* R + (1/3) * ð2 r (11)
Y restando y dividiendo por 2 se obtiene el valor de la otra:
F3 = ð3* R + (1/3) * ð2 r (12)
Las tres ecuaciones [10], [11] y [12] nos permiten conocer las tres ff.mm.mm. que estarán presentes en las ramas del núcleo, del transformador. Notamos, por de pronto, que son diferentes. Por lo tanto ahora podemos obtener los diagramas fasoriales.
Diagrama vectorial del transformador asimétrico en vacío
Sabemos, de acuerdo a la figura a que las dos ramas laterales tienen mayor reluctancia que la central, luego, por tener más volumen serán mayores sus pérdidas por histéresis y corrientes parásitas. La corriente de vacío del transformador es igual a la suma vectorial de la magnetizante y de la que cubre esas pérdidas; esta última componente está en fase con la tensión, de modo que en el diagrama vectorial de la figura 4 hemos tomado en fase con cada una de las tres tensiones la respectiva parte de la corriente de vacío que llamábamos IP.
La que corresponde a la rama central, la N° 2, es más pequeña que las otras dos por lo que hemos dicho más arriba. Si hacemos la suma vectorial de las tres corrientes en el diagrama de la figura b, vemos que la resultante no es nula, como correspondería a un sistema trifásico perfecto. En efecto, sumando OA con O C, se tiene el vector O D, al que sumamos el O B, que tiene sentido contrario, por lo que se resta y nos queda como resultante final el vector O F, pues el D F es igual a O B. De modo que el vector O F es la corriente Ir, resultante vectorial de las tres corrientes de pérdidas del transformador.

Diagrama vectorial de las corrientes de pérdidas en un transformador trifasico.
Como habiendo una resultante no se anularán las 3 ff.mm.mm. de las corrientes de pérdidas, tendremos que esta corriente resultante producirá una cierta cantidad de ampervueltas, y con ello, una f.m.m., de valor proporcional Ir y en fase con ella.
La figura 5 muestra el diagrama vectorial completo de un transformador trifásico en vacío, mostrando los efectos de las corrientes de perdidas Ir. Las tres tensiones y los tres flujos los hemos tomado desfasados entre sí de 120° y formando cada flujo un ángulo de 90° con la respectiva tensión. Además, tomamos 0 D, 0 H y 0 G sobre los vectores de flujo esos vectores representan las primeras partes de los segundos miembros de las ecuaciones [10], [11) y [12), ya conocidas. Paralelamente a O H se toman a partir de los puntos D, H y G, los segmentos que representan las segundas partes de las ff.mm.mm., según esas ecuaciones. Pero ahora hay que considerar la f.m.m. producida por Ir, que está en fase con la tensión E2. Esta f.m.m. aparece en cada rama, pero siempre paralelamente a la corriente I2, pues debe estar en fase con la corriente que la produce. Luego, desde los puntos J, M y K, que son los extremos adonde habíamos llegado; tomamos los vectores que representan esta nueva f.m.m., igual para las tres fases en sentido y magnitud.

Diagrama vectorial completo del trafo trifasico
Haciendo ahora la suma vectorial de las tres partes de que está formada cada f.m.m. resultante de cada rama, se tienen los vectores F1, F2 y F3, que se pueden ver en la figura, y que son distintos en magnitud y dirección para cada fase. Como vemos, la asimetría del núcleo provoca un desequilibrio en las corrientes magnetizantes y en las de pérdidas (diagrama de la fig. 4), resultando que las tres corrientes totales de vacío, o las respectivas ff.mm.mn. son distintas para las tras fases.
De estas consideraciones deducimos que la potencia que absorbe en vacío un transformador trifásico será distinta para cada fase, luego no podemos hacer el ensayo en vacío para una fase sola, y multiplicar después la potencia obtenida por tres, pues se cometería un error. Para determinar las pérdidas en el hierro de un transformador trifásico, puede realizarse el ensayo en vacío como en los monofásicos, pero siempre que se mida la potencia absorbida por las tres fases simultáneamente.
En cambio, para las pérdidas en el cobre, como los bobinados de las tres fases son iguales, y las corrientes de vacío se pueden despreciar para el ensayo en cortocircuito, podemos medir las pérdidas en el cobre en una sola fase y multiplicar por tres. Para ello, según se sabe, se mide la potencia que absorbe estando el secundario en cortocircuito, y aplicando tensión reducida al primario.
Diagrama vectorial con carga
El transformador trifásico con carga puede estudiarse como si fuera un conjunto de tres transformadores monofásicos; pues cada fase forma un circuito independiente en lo que respecta a la carga, tal como sucedía en el estudio particular de las redes trifásicas. Las diferencias entre las corrientes de vacío de las tres fases del transformador, no inciden mayormente en el estado de carga, ya que sabemos que el valor relativo de tales corrientes, comparadas con las de carga, es despreciable. Puede prescindirse, pues, de considerarlo, si se trata de hacer el estudio vectorial bajo carga.
Para estudiar el comportamiento del transformador bajo carga, recurrimos al diagrama vectorial. Se dispone de un sistema de tres bobinados que se conectan a las tres ramas de una red trifásica, luego tendremos tres ff.ee.mm inducidas en esos bobinados, las que estarán a 120° entre sí. Para simplificar el diagrama consideraremos una sola fase para el trazado completo, y simplificaremos las otras dos. La figura 6 muestra el diagrama vectorial de un transformador trifásico bajo carga óhmica. Para otros tipos de carga, ya sabemos cuáles son las diferencias que se tienen en la dirección del vector corriente secundaria.
Veamos la fase N° 1, por ejemplo. El flujo es un vector que está adelantado 90° con respecto a la f.e.m. inducida E1 o E2 en los bobinados primario y secundario de esa fase. Suponemos iguales los números de espiras de ambos bobinados, para simplificar el diagrama, con lo que esas dos ff.ee.mm. serán vectores iguales. En oposición a E1 tomamos el vector -E1.
La corriente de carga secundaria es I2, y produce caídas en el bobinado secundario, en fase y en cuadratura con la tensión en los bornes V2. Descontando a la f.e.rn. esas dos caídas se tiene la tensión en los bornes. V2, del secundario. Tomando el vector opuesto a la corriente secundaria, y sumándolo vectorialmente con la corriente de vacío I0, se obtiene la corriente total primaria, I1, que se ve en la figura. Y, finalmente, sumando a la f.e.m. -E1 las dos caídas, óhmica e inductiva en el primario, que están en fase y en cuadratura con la corriente primaria, respectivamente, se tiene la tensión en los bornes, V1, para este bobinado primario de la fase N°1. Si se observa esta parte de la figura 6 y se la compara con la del transformador monofásico se vera que es idéntica.

- Diagrama vectorial del transformador trifásico con carga.
Si hiciéramos la misma construcción para las fases 2 y 3 se obtendría una figura simétrica, donde cada tensión primaria sería un vector apartado en 120° de los otros. Para no complicar mucho el diagrama de la figura 6, sólo se ha dibujado, en las fases 2 y 3, la f.e.m. contraria á la inducida en los respectivos primarios, que son los vectores E1' y E1". A esas ff.ee.mm. les sumamos las caídas producidas por las corrientes totales primarias I1' e I2", como se ve en la figura, con lo que se encuentran las tensiones aplicadas a los primarios de las fases 2 (V1') y 3 (V1").
En lo que antecede se ha supuesto que la carga que tomaba cada fase del transformador era la misma, lo que sucede cuando el circuito de consumo tiene sus tres ramas iguales, en lo que respecta a las impedancias conectadas. Cualquier diferencia en la magnitud o en el ángulo propio de esas impedancias produce una diferencia en las corrientes secundarias, y por ende, en las caídas de cada fase, con lo que se alterarán las tensiones en los bornes secundarios.
Para otros estados de carga, tales como los de carga inductiva o capacitiva, o los de carga asimétrica; pueden ser estudiados siguiendo las normas dadas, y comparando siempre el diagrama con los monofásicos similares, pues se repiten estos últimos tres veces, desfasados en 120°. No insistiremos pues en ello, pero recordemos que las corrientes I0 de la figura 5 son distintas para las tres fases.
CONEXIONES TRIFASICAS
1.- Conexiones de transformador trifásico
Un transformador trifásico consta de tres transformadores monofásicos, bien separados o combinados sobre un núcleo. Los primarios y secundarios de cualquier transformador trifásico pueden conectarse independientemente en estrella( ð ) o en delta( ð ). Esto da lugar a cuatro conexiones posibles para un transformador trifásico.
1.1.- Conexión estrella( ð )- estrella( ð )
1.2.- Conexión estrella( ð )- delta( ð )
1.3.- Conexión delta( ð )- estrella( ð )
1.4.- Conexión delta( ð )- delta( ð )
1.1.- Conexión estrella( ð )- estrella( ð )
La conexión ð ðð de los transformadores se muestra en la figura 1.1.

Figura 1.1 Conexión ð ðð
En una conexión ð ðð, el voltaje primario de cada fase se expresa por VFP=VLP /ð3. El voltaje de la primera fase se enlaza con el voltaje de la segunda fase por la relación de espiras del transformador. El voltaje de fase secundario se relaciona, entonces, con el voltaje de la línea en el secundario por VLS =ð3 * VFS. Por tanto, la relación de voltaje en el transformador es
VLP / VLS = (ð3 * VFP) / (ð3 * VFS) = a
Se emplea en sistemas con tensiones muy elevadas, ya que disminuye la capacidad de aislamiento. Esta conexión tiene dos serias desventajas.
-
Si las cargas en el circuito del transformador estan desbalanceadas, entonces los voltajes en las fases del transformador se desbalancearan seriamente.
-
No presenta oposición a los armónicos impares(especialmente el tercero). Debido a esto la tensión del tercer armónico puede ser mayor que el mismo voltaje fundamental.
Ambos problemas del desbalance y el problema del tercer armónico, pueden resolverse usando alguna de las dos técnicas que se esbozan a continuación.
-
Conectar sólidamente a tierra el neutro primario de los transformadores. Esto permite que los componentes adicionales del tercer armónico, causen un flujo de corriente en el neutro, en lugar de causar gran aumento en los voltajes. El neutro también proporciona un recorrido de retorno a cualquier corriente desbalanceada en la carga.
-
Agregar un tercer embobinado(terciario) conectado en delta al grupo de transformadores. Esto permite que se origine un flujo de corriente circulatoria dentro del embobinado, permitiendo que se eliminen los componentes del tercer armónico del voltaje, en la misma forma que lo hace la conexión a tierra de los neutros.
De estas técnicas de corrección, una u otra deben usarse siempre que un transformador ð ðð se instale. En la practica muy pocos transformadores de estos se usan pues el mismo trabajo puede hacerlo cualquier otro tipo de transformador trifásico.
1.2.- Conexión estrella( ð )- delta( ð)
La conexión ð ðð de los transformadores trifásicos se ilustra en la figura 1.2.

Figura 1.2 Conexión ð ð ð
En esta conexión el voltaje primario de línea se relaciona con el voltaje primario de fase mediante VLP =ð3 * VFP, y el voltaje de línea secundario es igual al voltaje de fase secundario VLS = VFS. La relación de voltaje de cada fase es
VFP / VFS = a
De tal manera que la relación total entre el voltaje de línea en el lado primario del grupo y el voltaje de línea en el lado secundario del grupo es
VLP / VLS = (ð3 * VFP) / VFS
VLP / VLS = (ð3 * a)
La conexión ð ðð no tiene problema con los componentes del tercer armónico en sus voltajes, ya que ellos se consumen en la corriente circulatoria del lado delta(ð). Está conexión también es más estable con relación a las cargas desbalanceadas, puesto que la delta(ð) redistribuye parcialmente cualquier desbalance que se presente.
Esta disposición tiene, sin embargo, un problema. En razón de la conexión delta(ð), el voltaje secundario se desplaza 30º con relación al voltaje primario del transformador. El hecho de que un desplazamiento de la fase haya ocurrido puede causar problemas al conectar en paralelo los secundarios de dos grupos de transformadores. Los ángulos de fase de los transformadores secundarios deben ser iguales si se supone que se van a conectar en paralelo, lo que significa que se debe poner mucha atención a la dirección de desplazamiento de 30º de la fase, que sucede en cada banco de transformadores que van a ser puestos en paralelo.
En estados unidos se acostumbra hacer que el voltaje secundario atrase al primario en 30º. Aunque esto es lo reglamentario, no siempre se ha cumplido y las instalaciones más antiguas deben revisarse muy cuidadosamente antes de poner en paralelo con ellos un nuevo transformador, para asegurarse que los ángulos de fase coincidan.
La conexión que se muestra en la figura 1.2 hará que el voltaje secundario se atrase, si la secuencia es abc. Si la secuencia del sistema fase es acb, entonces la conexión que se ve en la figura 1.2 hará que el voltaje secundario se adelante al voltaje primario en 30º .
Se usa en los sistemas de transmisión de las subestaciones receptoras cuya función es reducir el voltaje. En sistemas de distribución es poco usual (no tiene neutro) se emplea en algunos ocasiones para distribución rural a 20 KV.
1.3.- Conexión delta( ð )- estrella( ð )
La conexión ð -ð de los transformadores trifásicos se ilustra en la figura 1.3.

Figura 1.3 Conexión ð ðð
En una conexión ð -ð , el voltaje de línea primario es igual al voltaje de fase primario, VLP=VFP, en tanto que los voltajes secundarios se relacionan por VLS =ð3 *VFS, por tanto la relación de voltaje línea a línea de esta conexión es
VLP / VLS = VFP / (ð3 * VFS)
VLP / VLS = a /ð3
Esta conexión tiene las mismas ventajas y el mismo desplazamiento de fase que el transformador ð ðð. La conexión que se ilustra en la figura 1.3, hace que el voltaje secundario atrase el primario en 30º,tal como sucedió antes.
Se usa en los sistemas de transmisión en los que es necesario elevar tensiones de generación. En sistemas de distribución industrial, su uso es conveniente debido a que se tiene acceso a dos tensiones distintas, de fase y línea.
1.4.- Conexión delta( ð )- delta( ð )
La conexión ð-ð se ilustra en la figura 1.4

Figura 1.4 conexión ð ðð
En una conexión de estas,
VLP = VFP
VLS = VFS
Así que la relación entre los voltajes de línea primario y secundario es
VLP / VLS = VFP / VFS = a
Esta conexión se utiliza frecuentemente para alimentar sistemas de alumbrado monofásicos y carga de potencia trifásica simultáneamente, presenta la ventaja de poder conectar los devanados primario y secundario sin desfasamiento, y no tiene problemas de cargas desbalanceadas o armónicas. Sin embargo, circulan altas corrientes a menos que todos los transformadores sean conectados con el mismo tap de regulación y tengan la misma razón de tensión.
Sistemas de por unidad para transformadores trifásicos.
El sistema de medición por-unidad puede aplicarse tanto a los transformadores trifásicos como a los monofásicos. La base monófasica se aplica a un sistema trifásico en bases por fase. Si el valor total de la base voltioamperio del grupo de transformadores se llama Sbase, entonces el valor de la base voltiamperio de uno de los transformadores S1F, base es
S1F, base = Sbase / 3
Y las bases de corriente e impedancia de fase del transformador son
IF, base = S1F, base / VF, base
IF, base = S base / 3 * VF, base
Z base = (VF, base)² / S1F, base
Z base = 3 * (VF, base)² / S base
Las magnitudes de línea en los grupos de transformadores trifásicos también pueden expresarse en por-unidad. La relación entre el voltaje base de línea y el voltaje base de fase del transformador dependen de la conexión de los devanados. Si los devanados se conectan en delta, VL,base = VF,base; mientras que si la conexión se hace en estrella, VL,base=ð3 * VF,base. La corriente de línea base en un transformador trifásico se expresa por.
IL,base = S base / ð3 * VL,base
La aplicación del sistema por-unidad en los problemas de los transformadores trifásicos es similar a su aplicación en los ejemplos para los monofásicos.
Funcionamiento en paralelo
Dos transformadores trifásicos funcionaran en paralelo si tienen la misma disposición de devanados (por ejemplo, estrella-triangulo), están conectados con la misma polaridad y tienen la misma secuencia de rotación de fases. Si dos transformadores (o dos bancos de transformadores) tienen la misma tensión nominal, las mismas relación de espiras, las mismas impedancias (en porcentaje) y las mismas relaciones entre reactancia y resistencia, se repartirán la corriente de carga proporcionalmente a sus potencias nominales, sin diferencia de fase entre las corrientes de los dos transformadores. Si cualquiera de las condiciones anteriores no se cumple, la corriente de carga puede no repartirse entre los dos transformadores en proporción a sus potencias nominales y puede haber una diferencia de fase entre las corrientes en los dos transformadores.
Transformadores de aislamiento:
Este tipo de transformadores es muy útil y confiable para alimentar instalaciones críticas como computadoras, sistemas médicos y sistemas de Telecomunicaciones, procesador de control e Instrumentación.
Los diseños de estos equipos se sobredimensionan de acuerdo al nivel de armónicos que presenta la instalación (Factor K)
Los sistemas de aislamiento usados en transformadores de potencia comprenden sistemas líquidos y sistemas gaseosos. En ambos casos se usa también algo de aislamiento sólido. Los sistemas líquidos incluyen aceite, que es el más usado, y askarel, que se usa para evitar la combustibilidad. Los sistemas gaseosos incluyen nitrógeno, aire y gases fluorados (por ejemplo, exafluoruro de azufre). Los gases fluorados se usan para evitar la combustibilidad y limitar los efectos secundarios de defectos internos.
El aislamiento principal separa el devanado de alta tensión del devanado de baja tensión. Este aislamiento soporta la tensión más elevada y ocupa el espacio más limitado; por esta razón, generalmente funciona con las solicitaciones más elevadas. Según la construcción, puede utilizarse el aislamiento de capas o el aislamiento de bobinas entre las distintas secciones de los devanados. El aislamiento de espiras se aplica a cada cable del conductor o a grupos de cables que formen una espira única.
Transformadores con aislamiento de aceite. El bajo costo, la elevada rigidez dieléctrica y la posibilidad de recuperación aun después de estar sometidos a solicitaciones dieléctricas excesivas, hacen del aceite mineral el material aislante más ampliamente usado en transformadores. El aceite se refuerza con aislamientos sólidos de varias maneras. El aislamiento principal, generalmente presenta barreras de aislamiento sólido alternando con espacios con aceite. El esfuerzo sobre el aceite es del 50 al 100% superior que el esfuerzo sobre el aislamiento sólido, debido a la constante dieléctrica relativamente baja del aceite. Por consiguiente, la solicitación del aceite limita la rigidez de la estructura. Los pequeños conductos de aceite pueden soportar solicitaciones más altas que los grandes conductos. Así barreras sólidas, convenientemente espaciadas, permiten una mejor utilización del espacio.
El aislamiento entre bobinas adyacentes generalmente es sólido, para proporcionar un soporte mecánico y dar una rigidez dieléctrica relativamente elevada respecto a las tensiones transitorias elevadas de corta duración. El aislamiento sólido a veces se usa entre capas de un devanado o entre devanados.
El aislamiento sólido de gran espesor se usa en los terminales de alta tensión en zonas de concentración de esfuerzos dieléctricos. La constante dieléctrica relativamente elevada del material sólido hace que la solicitación del sólido sea sólo la mitad o las dos terceras partes de la que habría si el aceite ocupara el mismo espacio.
La mayoría de materiales de aislamiento sólido usados en los transformadores de potencia son porosos, permitiendo eliminar, mediante el vacío, los gases y agua vaporizada, así como conseguir el relleno de todas las cavidades e intersticios con aceite. Cualquier pequeña cantidad de gas dejada inadvertidamente en el campo dieléctrico sufre una elevada solicitación dieléctrica (dos veces la que tendría el aceite) debido a la baja constante dieléctrica del gas. Como el gas encerrado, además de estar sometido a esfuerzos dieléctricos elevados, tiene una rigidez dieléctrica baja como consecuencia se tiene una pérdida importante de rigidez dieléctrica.
Los materiales sólidos usados frecuentemente, incluyen el papel impregnado con aceite, el papel impregnado con resinas, el cartón prensado, el algodón, la madera tratada con aceite al vacío y los esmaltes.
Los transformadores con aislamiento de askarel tienen construcciones similares a los transformadores con aislamiento de aceite. La constante dieléctrica relativamente elevada del askarel ayuda a transferir los esfuerzos dieléctricos a los elementos sólidos. El askarel tiene una posibilidad limitada de recuperarse después de haber estado sometido a solicitaciones dieléctricas excesivas y por ello la rigidez está limitada en campos eléctricos no uniformes. Los askarel se usan raramente por encima de las tensiones de funcionamiento de 34,5 kV. Los askarel son disolventes potentes y el material usado con ellos debe seleccionarse cuidadosamente, para evitar daño al material o contaminación del askarel.
Transformadores aislados mediante gases de flúor. Los gases de flúor tienen mejor rigidez dieléctrica y mayor capacidad de transferencia de calor que el nitrógeno o el aire. Tanto la rigidez dieléctrica como la capacidad de transferencia de calor aumentan con la densidad y los transformadores a base de gas flúor funcionan por encima de la presión atmosférica, en algunos casos hasta una presión calibrada de 3 atmósferas. El aislamiento de gas está .reforzado con aislamiento sólido usado en forma de barreras, aislamientos de capa, aislamiento de espira y aislamiento de terminales.
Generalmente resulta económico hacer funcionar los transformadores con aislamiento de gas flúor a temperaturas más elevadas que los transformadores aislados con aceite. Entre los materiales aislantes sólidos adecuados, se incluyen el vidrio, el amianto, la mica, las resinas para temperaturas elevadas, la cerámica, etc.
La solicitación dieléctrica sobre el gas es varias veces superior a la solicitación sobre el aislamiento sólido adyacente, en serie, de la estructura dieléctrica. Se necesita un cuidado especial al proyectar para evitar someter el gas a solicitaciones excesivas. Se ha usado el exafluoruro de azufre en transformadores con potencias nominales de hasta 25000 kVA y hasta 138 kV.
Los transformadores con aislamiento de nitrógeno y de aire están generalmente limitados a tensiones de funcionamiento de 15 kV y menores. Los transformadores con aislamiento de aire en sitios limpios, frecuentemente se ventilan a la atmósfera. En atmósferas contaminadas se necesita una construcción estanca y de ordinario se usa el nitrógeno a una presión aproximadamente igual a la atmosférica y a una temperatura de funcionamiento algo elevada.
Aislamiento interlaminar
El aislamiento interlaminar se consigue formando una capa de óxido natural sobre la superficie de la chapa magnética laminada plana o aplicando un revestimiento superficial. Evidentemente este tratamiento no reduce las corrientes parásitas en el interior de las chapas. Generalmente se consigue una mejora en la resistencia entre chapas recociendo la chapa bajo condiciones ligeramente oxidantes que aumentan el espesor del óxido superficial y cortando entonces las formas acabadas para los núcleos.
Los revestimientos o acabados de aislamiento pueden clasificarse ampliamente en orgánicos o inorgánicos:
- El aislamiento orgánico: consiste, en general, en esmaltes o barnices que se aplican a la superficie del acero para proporcionar una resistencia interlaminar.
La chapa magnética laminada plana con revestimiento de tipo orgánico no puede recibir un recocido de distensión sin perjudicar el valor aislante de la capa. Esta, sin embargo, resiste las temperaturas de funcionamiento normales. Algunos aislamientos orgánicos son apropiados sólo en núcleos refrigerados por aire, mientras que otros pueden ser apropiados para núcleos de transformadores tanto del tipo refrigerado por aire como los de baño de aceite. El espesor de este tipo de aislamiento es de aproximadamente de 2,5 ð m.
- El aislamiento inorgánico: se caracteriza, en general, por una elevada resistencia y por la capacidad de resistir las temperaturas necesarias para el recocido de distensión. Esta ideado para núcleos de transformadores refrigerados por aire o en baño de aceite.
Descargar
| Enviado por: | Jasón |
| Idioma: | castellano |
| País: | Panamá |