Matemáticas
Límite
Límite
Antes de empezar, conviene recordar el concepto de "tender". Cuando decimos, por ejemplo, a qué valor tiende la función nos referimos a qué valor se acerca la función (cabe aclarar que hablamos de "acercarse", pero no de "llegar" a ese valor).
Definición intuitiva de límite: Si los valores de f(x) pueden hacerse arbitrariamente cercanos a un número (único) L, cuando x se acerca a un número A por ambos lados, entonces decimos que "el límite de f(x) es L cuando x tiende a A"
Lim f(x)=L
x— A
Definición formal de límite: la función f(x) tiene como límite L en el punto de acumulación x=A cuando el valor absoluto (el módulo) de la diferencia entre los valores f(x) y L se puede hacer tan pequeño como se quiera con tal de considerar valores de x suficientemente próximos a A.
Lim f(x)=L
x— A
... si para todo E 0, existe un § 0 tal que /f(x)-L/ E cuando /x-A/ §
Quizás te sirva verlo mejor en un ejemplo: hacemos la tabla de valores de la función f(x)= x^2+1.
-
x ................f(x)= x^2+1
-
2,2..................5,84
-
2,1................ .5,41
-
2,01................5,04
-
2,001..............5,004
-
1,9..................4,61
-
1,99................4,96
-
1,999..............4,996
Los valores de x que están en verde son aquellos que se aproximan a 2 por la derecha, por valores mayores que 2. Los que están en rosa son los valores de x que se aproximan a 2 por la izquierda, por valores menores que 2.
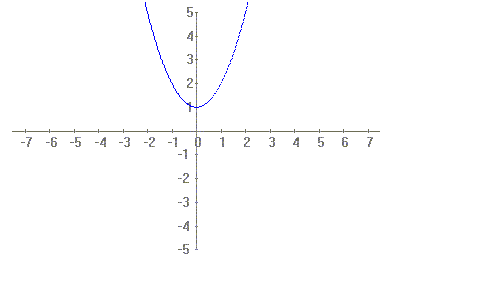
Como podés ver en el gráfico, a medida que los valores de x se aproximan cada vez más a 2, tanto por la derecha como por la izquierda, los valores que determina la función se aproximan cada vez más al númerp 5. Esto se expresa diciendo que la función f(x)= x^2+1 tiene límite 5 en el punto x=2 o cuando x tiende a 2, que se indica simbólicamente:
Lim f(x^2+1)=5
x— 2
Eso se lee así: límite de (x^2+1) para x tendiendo a 2 es igual a 5. También se dice que dicha función tiende a 5 cuando x tiende a 2, que se indica así: (x^2+1)— 5 cuando x— 2
Teoremas sobre límites
Teorema 1: límite de una función constante.
Sea f(x)=k(constante), entonces:
Lim f(x)=Limk=k
x— A.....x— A
Teorema 2: límite de f(x)=x cuando x— A
Sea f(x)=x, entonces
Lim f(x)=Limx=A
x— A.....x— A
Teorema 3: límite de una función multiplicada por una constante
Sea k una constante y f(x) una función dada, entonces:
Lim kf(x)=kLimf(x)=A
x— A.....x— A
Teorema 4: límite de una suma, resta, producto y cociente de funciones
Supongamos que.. Lim f(x)=L1 y Lim g(x)=L2
x— A.... ........x— A
Entonces:
Lim (f(x)+g(x))=L1 +L2
x— A...
Lim (f(x)-g(x))=L1-L2
x— A.
........ .Lim (f(x)*g(x))=L1*L2
..x— A.
..........Lim (f(x)÷g(x))=L1÷L2
...x— A
.
Teorema 5: límite de una potencia
Sea n un número entero positivo, entonces:
Lim x^n=a^n
x— A...
Teorema 6: límite de un polinomio
Sea f(x) una función polinominal, entonces:
Lim f(x)=f(A)
x— A...
Teorema 7: límite de una función racional
Sea f(x)= p(x)÷q(x) un cociente de polinomios, entonces:
Lim f(x)=p(A)÷q(A) (si q(A) no es cero)
x— A...
Teorema 8: límite de una función que contiene un radical
Sea A 0 y n es cualquier entero positivo, o bien, si A 0 y n es un entero positivo impar, entonces:
Lim x^1÷n=A^1÷n
x— A...
Teorema 9: límite de una función compuesta
Supongamos que.. Lim g(x)=L y Lim f(x)= f(L)
x— A.... ......x— L
Entonces:
Lim f (g(x))= f(L)
x— A..
Propiedades de los límites:
1) Si dos funciones f(x) y g(x) toman valores iguales en un entorno reducido de un punto de acumulación x=a y una de ellas tiene límite l en ese punto, la otra también tiene límite l en a.
2) Si una función tiene límite en un punto, ese límite es único. Una función no puede tener dos límites distintos en un punto.
3) Si una función tiene límite l en un punto, en un entorno reducido del mismo, la función toma valores menores que cualquier número mayor que el límite y mayores que cualquier número menor que el límite
Corolario1: si una función tiene en un punto un límite distinto de cero, en un entorno reducido del punto, la función determina valores del mismo signo que su límite
Corolario2: toda función que tiene límite finito en un punto, está acotada en un entorno reducido del mismo
4) Si en un entorno reducido de un punto, los valores que determina la función están comprendidos entre los de otras dos funciones que tienen el mismo límite en ese punto, ella también tiene ese mismo límite en el punto.
Límites laterales:
Cuando las condiciones que exigen la existencia de límite de una función en un punto a, se verifican solamente para valores de x menores que a, se dice que existe límite por la izquierda de a.
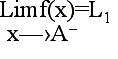
Si las condiciones se verifican únicamente para valores de x mayores que a se dice que existe límite por la derecha de a.
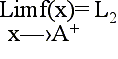
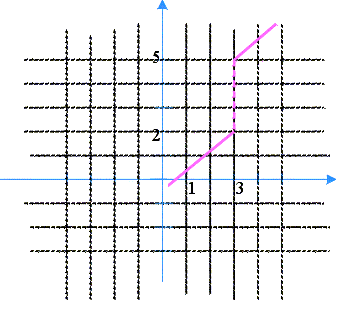
Tomemos el siguiente ejemplo de la función discontinua f(x):
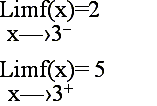
Descargar
| Enviado por: | Issg |
| Idioma: | castellano |
| País: | Venezuela |
