Física
Leyes de los choques
LEYES DE LOS CHOQUES
Introducción y Objetivo:
En esta práctica se estudiará la conservación del ímpetu o momento lineal y de la energía en diferentes tipos de colisiones.
La conservación del momento lineal (p= m·v) es un concepto físico muy importante. Sin embargo, este experimento es difícil de realizar en un laboratorio físico debido a la influencia de las fuerzas de rozamiento.
Un carril neumático es uno de los mejores métodos para investigar el momento lineal. Unos “coches” o planeadores de aluminio deslizando sobre una corriente de aire que sale del carril, elimina las fuerzas de rozamiento, condición indispensable para la conservación del momento lineal o ímpetu.
En ausencia de rozamiento y otras fuerzas externas, el momento lineal de un sistema de dos planeadores se conservará durante la colisión de los dos planeadores. Gracias a este montaje, el momento lineal total del sistema será el mismo antes y después del choque. Midiendo las velocidades de los “coches” de iguales y de diferentes masas antes y después de la colisión, y así se puede investigar la conservación del ímpetu. Además, si el choque es perfectamente elástico, toda la energía acumulada durante la deformación de los cuerpos se recupera cuando vuelven a su forma original. Las energías cinéticas antes y después del choque son iguales.
Material:
-
Carril neumático de 2m de largo
-
Soplador eléctrico
-
Dos fotopuertas
-
Ordenador Apple Macintosh
-
Interfaz MacTimer
-
Dos planeadores de aluminio anodizado, con una masa de 180±1 g
-
Cuatro pesas de 50 g para los planeadores
-
Dos banderas de 100 mm de largo
-
Dos bandas de goma parachoques
-
Lámina parachoques
-
Tubo con cera
-
Aguja
Parte experimental:
- Choque elástico (uno de los planeadores en reposo)
Se sitúa un planeador con parachoques en reposo, v2 = 0, entre las dos fotopuertas aproximadamente en el centro del carril.
Se coloca otro planeador también con parachoques, en un extremo del carril, a la izquierda del primero y se impulsa contra el planeador en reposo (ambos han de estar adecuadamente equilibrados).
Se preparan las dos fotopuertas para medir el tiempo de tránsito de cada planeador. Se elige la derecha como dirección positiva y se miden las velocidades (magnitud y sentido).
En la Tabla 1 se anotan los valores de las masas y las velocidades de cada planeador antes y después de la colisión y se calculan los valores del momento y la energía cinética inicial y final.
Se empieza con el planeador 1 cargado con 200g y se van tomando las velocidades. Se va reduciendo la carga y se repite el proceso con el planeador 2.
Planeador 1 = 180g + 30g (sin pesas adicionales)
Planeador 2 = 180g + 30g (sin pesas adicionales)
Tabla 1: Velocidades de los planeadores antes y después de la colisión variando la masa.
| m1 (g) | m2 (g) | v1 (m/s) | v2 (m/s) | v'1 (m/s) | v'2 (m/s) |
| +200 | +0 | 0.5811 | 0.0000 | 0.5530 | 0.7331 |
| +100 | +0 | 0.4107 | 0.0000 | 0.0000 | 0.3250 |
| +0 | +0 | 0.5305 | 0.0000 | 0.1445 | 0.2369 |
| +0 | +200 | 0.6353 | 0.0000 | -0.3639 | 0.2680 |
| +0 | +100 | 0.6136 | 0.0000 | -0.2905 | 0.1811 |
Se calcula el ímpetu después de la colisión p' =p1'+ p2' y antes de la colisión p= p1 + p2 para realizar la representación gráfica. (Sabiendo que pi = mi·vi ).
Gráfica 1:Ímpetu antes (p) y después (p') de la colisión de los planeadores. Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 1 (se considera a “p” como variable “x” y a “p'” como variable “y”)
| p1 (kg·m/s) | p2(kg·m/s) | p1'(kg·m/s) | p2'(kg·m/s) | p (kg·m/s) | p'(kg·m/s) |
| 0.238 | 0.000 | 0.227 | 0.154 | 0.238 | 0.381 |
| 0.127 | 0.000 | 0.000 | 0.068 | 0.127 | 0.068 |
| 0.111 | 0.000 | 0.030 | 0.050 | 0.111 | 0.080 |
| 0.133 | 0.000 | -0.076 | 0.110 | 0.133 | 0.034 |
| 0.129 | 0.000 | -0.061 | 0.056 | 0.129 | -0.005 |
ii) Se calculan los siguientes valores (siendo p≡x , p'≡y)
∑ x = 0.738
∑ x2 = 0.119424
∑ y = 0.558
∑ y2 = 0.157366
∑ x·y = 0.112071
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 0.0104952
σy = ∑ y2 - 1/N (∑ y)2 = 0.0950932
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 0.0297102
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 2.830836954
n = [∑ y-m· ∑ x] / N = -0.306231534
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 3.662822643 · 10-3
s2m = 0.348999794 ; sm = 0.588217471
s2n = 7.325645286 · 10-4
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.94044951
** La ecuación de la recta será: y = 2.830836954· x - 0.306231534
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 0.120
P2* x = 0.140
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.033
y2 = 0.090
P1 (0.120, 0.033) P2 (0.140, 0.090)
Se marcan los puntos y se traza la recta que los une.
El valor de la pendiente es: m ≈ 2.831 , y su incertidumbre es: Δm ≈ 0.6.
Así, m = 2.4 ± 0.6
Observando el valor de la pendiente, se aprecia que no se ajusta al valor de 1, es decir, a la conservación del ímpetu.
Debe estudiarse ahora la conservación de la energía, sabiendo que:
E =1/2·m1·v12 + 1/2·m2·v22 ; E' =1/2·m1·v1'2 + 1/2·m2·v2'2
Gráfica 2:Energía antes (E) y después (E') de la colisión de los planeadores. Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 1 (se considera a “E” como variable “x” y a “ E' ” como variable “y”)
| E (J) | E' (J) |
| 0.069 | 0.119 |
| 0.026 | 0.011 |
| 0.030 | 8.090·10-3 |
| 0.042 | 0.029 |
| 0.040 | 0.014 |
ii) Se calculan los siguientes valores (siendo E≡x , E'≡y)
∑ x = 0.207
∑ x2 = 9.701·10-3
∑ y = 0.18109
∑ y2 = 0.015384448
∑ x·y = 0.0105177
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 1.1312·10-3
σy = ∑ y2 - 1/N (∑ y)2 = 8.825731·10-3
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 3.020274·10-3
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 2.670238685
n = [∑ y-m· ∑ x] / N = -0.074329881
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 2.538931731 · 10-4
s2m = 0.224445874 ; sm = 0.473757188
s2n = 5.077863462 · 10-5
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.955970413
** La ecuación de la recta será: y = 2.670238685· x - 0.074329881
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 0.025
P2* x = 0.065
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = -7.574·10-3
y2 = 0.099
P1 (0.025, -7.574·10-3) P2 (0.065, 0.099)
Se marcan los puntos y se traza la recta que los une.
El valor de la pendiente es: m ≈ 2.670 , y su incertidumbre es: Δm ≈ 0.5.
Así, m = 2.7 ± 0.5
Observando el valor de la pendiente, se aprecia que no se ajusta al valor de 1, es decir, a la conservación del ímpetu.
Existe una pequeña fuerza de fricción que está presente durante el experimento. Esta fuerza introduce en las medidas un error aleatorio. El efecto de esta fuerza puede detectarse en el análisis gráfico en cuanto a que el valor de la pendiente no se ajusta totalmente a la conservación del ímpetu o de la energía cinética.
Por lo tanto, centrándose en los resultados experimentales no se puede asegurar que el choque es completamente elástico. Así, el cambio en la energía cinética se debe a errores como la fuerza de rozamiento (debida a la capa de aire que mantiene a cada planeador) o como defectos del montaje experimental o deficiencias en la ejecución de la experiencia.
- Choque elástico (los dos planeadores en movimiento)
Con los dos planeadores en movimiento y en direcciones opuestas, se lanza uno contra el otro desde los extremos del carril de forma que la colisión se produzca entre las dos fotopuertas.
Se repiten las medidas del apartado 1.1 variando las masas. Se completa una tabla con los resultados (Tabla 2).
Planeador 1 = 180g + 30g (sin pesas adicionales)
Planeador 2 = 180g + 30g (sin pesas adicionales)
Tabla 2: Velocidades de los planeadores antes y después de la colisión variando la masa.
| m1 (g) | m2 (g) | v1 (m/s) | v2 (m/s) | v'1 (m/s) | v'2 (m/s) |
| +0 | +0 | 0.6496 | -0.3877 | -0.1356 | 0.3850 |
| +200 | +0 | 0.5160 | -0.4537 | -0.1407 | 0.4047 |
| +100 | +0 | 0.5660 | -0.4529 | -0.1719 | 0.4067 |
| +0 | +200 | 0.5792 | -0.4545 | -0.5125 | 0.2219 |
| +0 | +100 | 0.6814 | -0.4240 | -0.3575 | 0.3116 |
Se calcula el ímpetu después de la colisión p' =p1'+ p2' y antes de la colisión p= p1 + p2 para realizar la representación gráfica. (Sabiendo que pi = mi·vi ).
Gráfica 3: Ímpetu antes (p) y después (p') de la colisión de los planeadores. Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 2 (se considera a “p” como variable “x” y a “p'” como variable “y”)
| p1 (kg·m/s) | p2(kg·m/s) | p1'(kg·m/s) | p2'(kg·m/s) | p (kg·m/s) | p'(kg·m/s) |
| 0.136 | -0.081 | -0.028 | 0.081 | 0.055 | 0.053 |
| 0.212 | -0.095 | -0.058 | 0.166 | 0.117 | 0.108 |
| 0.175 | -0.095 | -0.053 | 0.126 | 0.080 | 0.073 |
| 0.122 | 0.186 | -0.108 | 0.047 | 0.308 | -0.061 |
| 0.143 | 0.131 | -0.075 | 0.065 | 0.274 | -0.010 |
ii) Se calculan los siguientes valores (siendo p≡x , p'≡y)
∑ x = 0.834
∑ x2 = 0.193054
∑ y = 0.163
∑ y2 = 0.023623
∑ x·y = -1.37·10-4
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 0.0539428
σy = ∑ y2 - 1/N (∑ y)2 = 0.0183092
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = -0.0273254
iv) Los parámetros de ajuste serán:
m = σx·y /σx = -0.506562507
n = [∑ y-m· ∑ x] / N = 0.117094626
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 1.489058958 · 10-3
s2m = 0.027604406 ; sm = 0.166145737
s2n = 2.978117916 · 10-4
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = -0.869491019
** La ecuación de la recta será: y = -0.506562507· x + 0.117094626
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 0.020
P2* x = 0.300
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.107
y2 = -0.035
P1 (0.020, 0.107) P2 (0.300, -0.035)
Se marcan los puntos y se traza la recta que los une.
El valor de la pendiente es: m ≈ -0.507 , y su incertidumbre es: Δm ≈ 0.2.
Así, m = -0.5 ± 0.2
Observando el valor de la pendiente, se aprecia que no se ajusta totalmente (aunque más que en el caso anterior) al valor de 1, es decir, a la conservación del ímpetu.
Debe estudiarse ahora la conservación de la energía, sabiendo que:
E =1/2·m1·v12 + 1/2·m2·v22 ; E' =1/2·m1·v1'2 + 1/2·m2·v2'2
Gráfica 4:Energía antes (E) y después (E') de la colisión de los planeadores. Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 2 (se considera a “E” como variable “x” y a “ E' ” como variable “y”)
| E (J) | E' (J) |
| 0.060 | 0.017 |
| 0.076 | 0.021 |
| 0.071 | 0.022 |
| 0.078 | 0.038 |
| 0.077 | 0.028 |
ii) Se calculan los siguientes valores (siendo E≡x , E'≡y)
∑ x = 0.362
∑ x2 = 0.02643
∑ y = 0.126
∑ y2 = 3.442·10-3
∑ x·y = 9.298·10-3
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = -2.212·10-4
σy = ∑ y2 - 1/N (∑ y)2 = -2.668·10-4
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = -1.756·10-4
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.793851717
n = [∑ y-m· ∑ x] / N = -0.032274864
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = -4.246654611 · 10-5
s2m = 0.191982577 ; sm = 0.438158164
s2n = -8.493309222·10-6
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.722834774
** La ecuación de la recta será: y = 0.793851717· x - 0.032274864
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 0.050
P2* x = 0.080
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 7.418·10-3
y2 = 0.031
P1 (0.050, 7.418·10-3) P2 (0.080, 0.031)
Se marcan los puntos y se traza la recta que los une.
El valor de la pendiente es: m ≈ 0.794 , y su incertidumbre es: Δm ≈ 0.4.
Así, m = 0.8 ± 0.4
Observando el valor de la pendiente, se aprecia que se ajusta bastante (teniendo en cuenta su incertidumbre) al valor de 1, es decir, a la conservación del ímpetu.
- Choque plástico
Uno de los planeadores llevará un tubo con cera y el otro una aguja. (Ambos planeadores deben estar adecuadamente equilibrados).
Con uno de los planeadores en reposo, v2 = 0, situado entre las fotopuertas, se lanza el otro desde uno de los extremos del carril. Se toma la velocidad inicial(v1) y final (v') que será la misma para los dos planeadores (se tomará la velocidad dada por el paso de la primera bandera)
Se repiten las medidas de los apartados anteriores variando las masas. (Los resultados se anotan en la Tabla 3).
Planeador 1 = 180g + 30g (sin pesas adicionales)
Planeador 2 = 180g + 30g (sin pesas adicionales)
Tabla 3: Velocidades de los planeadores antes y después de la colisión variando la masa.
| m1 (g) | m2 (g) | v1 (m/s) | v2 (m/s) | v' (m/s) |
| +200 | +0 | 0.5631 | 0.0000 | 0.3367 |
| +100 | +0 | 0.6755 | 0.0000 | 0.3654 |
| +0 | +0 | 0.7383 | 0.0000 | 0.3308 |
| +0 | +200 | 0.7970 | 0.0000 | 0.1814 |
| +0 | +100 | 0.7986 | 0.0000 | 0.2250 |
Se calcula el ímpetu después de la colisión p' =p1'+ p2' y antes de la colisión p= p1 + p2 para realizar la representación gráfica. (Sabiendo que pi = mi·vi ).
Gráfica 5: Ímpetu antes (p) y después (p') de la colisión de los planeadores. Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 3 (se considera a “p” como variable “x” y a “p'” como variable “y”)
| p1 (kg·m/s) | p2(kg·m/s) | p'(kg·m/s) | p (kg·m/s) | p'(kg·m/s) |
| 0.231 | 0.000 | 0.209 | 0.231 | 0.209 |
| 0.209 | 0.000 | 0.190 | 0.209 | 0.190 |
| 0.155 | 0.000 | 0.139 | 0.155 | 0.139 |
| 0.167 | 0.000 | 0.112 | 0.167 | 0.112 |
| 0.168 | 0.000 | 0.117 | 0.168 | 0.117 |
** Nota: Sólo hay un p' ya que después de la colisión, los dos cuerpos se comportan como uno solo de masa la suma de m1 y m2 y con una única velocidad (v')
ii) Se calculan los siguientes valores (siendo p≡x , p'≡y)
∑ x = 0.93
∑ x2 = 0.17718
∑ y = 0.767
∑ y2 = 0.125335
∑ x·y = 0.147894
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 4.2·10-3
σy = ∑ y2 - 1/N (∑ y)2 = 7.6772·10-3
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 5.232·10-3
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 1.245714286
n = [∑ y-m· ∑ x] / N = -0.078302857
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 3.865409524 · 10-4
s2m = 0.09203356 ; sm = 0.303370334
s2n = 7.730819048· 10-5
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.921386114
** La ecuación de la recta será: y = 1.245714286· x - 0.078302857
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 0.100
P2* x = 0.240
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.046
y2 = 0.221
P1 (0.100, 0.046) P2 (0.240, 0.221)
Se marcan los puntos y se traza la recta que los une.
El valor de la pendiente es: m ≈ 1.246 , y su incertidumbre es: Δm ≈ 0.3.
Así, m = 1.2 ± 0.3
Observando el valor de la pendiente, se aprecia que se ajusta bastante al valor de 1, es decir, a la conservación del ímpetu.
Debe estudiarse ahora la conservación de la energía, sabiendo que:
E =1/2·m1·v12 + 1/2·m2·v22 ; E' =1/2·m1·v1'2 + 1/2·m2·v2'2
Gráfica 6:Energía antes (E) y después (E') de la colisión de los planeadores. Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 3 (se considera a “E” como variable “x” y a “ E' ” como variable “y”)
| E (J) | E' (J) |
| 0.065 | 0.035 |
| 0.071 | 0.035 |
| 0.057 | 0.023 |
| 0.067 | 0.010 |
| 0.067 | 0.013 |
ii) Se calculan los siguientes valores (siendo E≡x , E'≡y)
∑ x = 0.327
∑ x2 = 0.021493
∑ y = 0.116
∑ y2 = 3.248·10-3
∑ x·y = 7.612·10-3
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 1.072·10-4
σy = ∑ y2 - 1/N (∑ y)2 = 5.568·10-4
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 2.56·10-5
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.23880597
n = [∑ y-m· ∑ x] / N = 7.582089552·10-3
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 1.835621891· 10-4
s2m = 1.712333853 ; sm = 1.30856175
s2n = 3.671243782·10-5
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = -0.9849036
** La ecuación de la recta será: y = 0.23880597· x + 7.582089552·10-3
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 0.025
P2* x = 0.075
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.014
y2 = 0.025
P1 (0.025, 0.014) P2 (0.075, 0.025)
Se marcan los puntos y se traza la recta que los une.
Observando los resultados de E y E' se muestran las fracciones aproximadas de Energía cinética transformada en otro tipo de energía tras la colisión:
| Energía transformada |
| 46% |
| 51% |
| 60% |
| 85% |
| 81% |
Energía transformada (media) ≈ 65% de la Energía cinética inicial.
LEY DE CONSERVACIÓN DE LA ENERGÍA MECÁNICA
Introducción y Objetivo:
En un sistema conservativo ideal, la energía se transfiere entre energía cinética y potencial. En tal sistema, la suma de la energía cinética y la energía potencial es constante, tal y como se expresa en la ley de la energía mecánica. Sin embargo, en los sistemas reales, el rozamiento está siempre presente y así, este sistema no es conservativo. Es decir, alguna energía se pierde como resultado del trabajo hecho en contra de estas fuerzas de rozamiento. Incluso así, la energía total se conserva.
El objetivo de esta práctica es la comprobación de la ley de conservación de la energía mecánica mediante el disco de Maxwell.
Material:
-
Disco de Maxwell (m=530g, radio (sin hilo)= 2.75mm, radio (con hilo)= 3.00 mm)
-
Cronómetro digital
-
Puerta fotoeléctrica
-
Dispositivo y cable disparador
-
Regla graduada
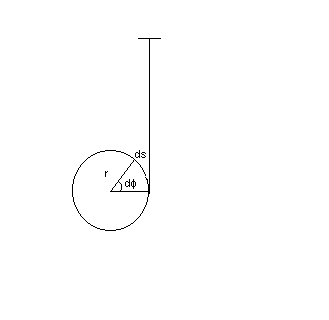
Parte experimental:
Tabla 1: Valores de t y Δt en función de la altura.
| Altura (s) (mm) | Tiempo (t) (s) | Tiempo medio (s) | Δt (s) | Δt medio (s) |
| 500 | 6.416 | 6.376 | 0.298 | 0.302 |
| 6.336 | 0.305 | |||
| 400 | 5.663 | 5.704 | 0.330 | 0.329 |
| 5.745 | 0.328 | |||
| 350 | 5.344 | 5.353 | 0.355 | 0.352 |
| 5.361 | 0.349 | |||
| 300 | 5.198 | 5.071 | 0.372 | 0.374 |
| 4.944 | 0.376 | |||
| 200 | 4.179 | 4.081 | 0.459 | 0.464 |
| 3.983 | 0.469 | |||
| 100 | 2.920 | 2.903 | 0.640 | 0.638 |
| 2.885 | 0.636 |
1 m · g
Partiendo de la ecuación : s(t) = ---- · -------------- · t2
2 m + (Iz/r2)
se puede comprobar si la energía mecánica se conserva siempre y cuando ésta
se cumpla. Tomando logaritmos a ambos lados de la igualdad se puede
linealizar la ecuación representando en el eje de abscisas la altura (s) y en el
eje de ordenadas el tiempo (t). Para que el método gráfico confirme la
conservación de la energía, el valor de la pendiente de be ajustarse a 1.
Gráfica 1:Tiempo (t) frente a longitud (s). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 1 (se considera a “log s” como variable “x” y a “log t” como variable “y”)
| log s (mm) | log t (s) |
| 2.699 | 0.805 |
| 2.602 | 0.756 |
| 2.544 | 0.729 |
| 2.477 | 0.705 |
| 2.301 | 0.611 |
| 2.000 | 0.463 |
ii) Se calculan los siguientes valores (siendo log s≡x , log t≡y)
∑ x = 14.623
∑ x2 = 35.957071
∑ y = 4.069
∑ y2 = 2.835717
∑ x·y = 10.072579
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 0.318382833
σy = ∑ y2 - 1/N (∑ y)2 = 0.076256833
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 0.155747833
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.489184142
n = [∑ y-m· ∑ x] / N = -0.514056618
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 1.686573508· 10-5
s2m = 5.29731296 · 10-5 ; sm = 7.278264189 · 10-3
s2n = 2.810955847·10-6
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.999557561
** La ecuación de la recta será: y = 0.489184142· x - 0.514056618
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 1.500
P2* x = 2.650
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.220
y2 = 0.782
P1 (1.500, 0.220) P2 (2.650, 0.782)
Se marcan los puntos y se traza la recta que los une.
El valor de la pendiente es: m ≈ 0.5 y su incertidumbre es Δm ≈ 0.7·10-3
El valor esperado (m≈1) no se encuentra entre el intervalo 0.5-0.7·10-3 , 0.5+0.7·10-3
m· g ds
Utilizando la ecuación v(t) = ------------- · t = --------
m + (Iz/r2) dt
se puede hacer una estimación del valor de Iz; para ello se representa gráficamente “v” frente a “t”.
Gráfica 2:Velocidad (v) frente al tiempo (t). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 1 hallándose las velocidades correspondientes (se considera a “t” como variable “x” y a “v” como variable “y”)
| Tiempo (s) | Velocidad (m/s) |
| 6.527 | 7.66·10-2 |
| 5.869 | 6.82·10-2 |
| 5.529 | 6.33·10-2 |
| 5.258 | 5.71·10-2 |
| 4.313 | 4.64·10-2 |
| 3.222 | 3.10·10-2 |
ii) Se calculan los siguientes valores (siendo t≡x , v≡y)
∑ x = 30.718
∑ x2 = 164.246548
∑ y = 0.3426
∑ y2 = 0.02090006
∑ x·y = 1.8504567
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 6.980627334
σy = ∑ y2 - 1/N (∑ y)2 = 1.3376·10-3
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 0.0964589
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.013818084
n = [∑ y-m· ∑ x] / N = -0.013643987
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 1.180686605· 10-6
s2m = 1.691376073· 10-7 ; sm = 4.112634282 · 10-4
s2n = 1.967811008·10-7
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.998233058
** La ecuación de la recta será: y = 0.013818084· x - 0.013643987
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 2.000
P2* x = 6.000
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 1.400·10-2
y2 = 6.926·10-2
P1 (2.000, 1.400·10-2 ) P2 (6.000, 6.926·10-2)
Se marcan los puntos y se traza la recta que los une.
El valor de la pendiente es: m ≈ 0.0140 y su incertidumbre es Δm ≈ 0.0004
m·g
Fijándose en la ecuación : v(t) = ------------- · t se deduce que:
m + (Iz/r2)
m·g
m (pendiente)= -------------- , y por lo tanto las unidades de la pendiente son las de
m + (Iz/r2)
una aceleración, es decir, m/s2.
De esto, se puede deducir el valor de Iz:
0.530·9.81 5.199 4.679·10-5
0.014 = -------------------- ; 0.014= -------------------------- ; 0.014= ---------------- ;
0.530+(Iz/9·10-6) (4.77·10-6+Iz)/9·10-6 4.77·10-6+Iz
Iz ≈ 3.34·10-3 kg·m2
Se elaborará una gráfica energía - tiempo.
E= Ep+Ec
Ec=Et+Er ; Ec=1/2·(m+Iz/r2)·v2(t)
Et =1/2·m·v2(t)
Er= 1/2·Iz·ω2(t)
Ep=-m·g·s(t)
Gráfica 3:Energía (E) frente al tiempo (t). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 1 hallándose las velocidades correspondientes (se considera a “t” como variable “x” y a “E” como variable “y”)
| Tiempo (s) | Energía (J) |
| 6.527 | -1.243 |
| 5.869 | -0.950 |
| 5.529 | -0.809 |
| 5.258 | -0.688 |
| 4.313 | -0.374 |
| 3.222 | -0.076 |
ii) Se calculan los siguientes valores (siendo t≡x , E≡y)
∑ x = 30.718
∑ x2 = 164.246548
∑ y = -4.14
∑ y2 = 3.721026
∑ x·y = -23.63701
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 6.980627334
σy = ∑ y2 - 1/N (∑ y)2 = 0.864426
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = -2.44159
iv) Los parámetros de ajuste serán:
m = σx·y /σx = -0.349766558
n = [∑ y-m· ∑ x] / N = 1.100688192
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 2.609865962· 10-3
s2m = 3.738726979· 10-4 ; sm = 0.019335788
s2n = 4.349776603·10-4
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = -0.993943276
** La ecuación de la recta será: y = -0.349766558· x +1.100688192
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 3.500
P2* x = 6.000
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = -0.123
y2 = -0.998
P1 (2.000, 1.400·10-2 ) P2 (6.000, 6.926·10-2)
Se marcan los puntos y se traza la recta que los une.
El valor de la pendiente no se ajusta suficientemente a cero. Como conclusión, se observa que los resultados experimentales para demostrar la conservación de la energía mecánica no son los más deseados.
Descargar
| Enviado por: | Vicente |
| Idioma: | castellano |
| País: | España |
