Ingeniero en Electrónica
Ingeniería
EJERCICIO - 1
Generamos aleatoriamente en Matlab un proceso de primer orden.
» [n,d]=rmodel(1)
n = 0 -1.6656
d = 1.0000 0.6488
» printsys(n,d)
num/den =
-1.6656
-----------
s + 0.64884
a) Estabilidad en bucle cerrado del proceso continuo
Para ver la dinámica natural del sistema en bucle abierto, dibujamos su respuesta frente a un escalón unitario. En Matlab, escribimos:
» step(n,d)
Vemos que el sistema es estable en bucle abierto, aunque con ganancia negativa. Para estudiar el rango de estabilidad en bucle cerrado escribimos:
» rlocus(n,d)
En el lugar de las raíces vemos que el sistema en bucle cerrado será estable para toda K negativa, y para K positivas hasta un valor límite. Para conocer la K límite escribimos:
» [k,poles]=rlocfind(n,d)
Select a point in the graphics window
Sobre el gráfico seleccionamos el origen como polo de bucle cerrado y la función nos da el valor de la K para ese polo.
selected_point = 0.0000 - 0.0058i
k = 0.3896
poles = 2.6353e-005
Por lo tanto el rango de estabilidad es K"[-" , 0.3896]
Con el programa CC esto es más sencillo pues podemos aplicar el criterio de Routh directamente. Introducimos la función de transferencia en bucle abierto y ejecutamos el comando Routh
CC>gba = -1.6566 / (s + 0.6488)
CC>routh,gba
Stable for gain ranges: - infinity to 0.3916456
Este resultado es más exacto que el de Matlab obtenido gráficamente.
b) Estabilidad en bucle cerrado del equivalente discreto del proceso
Usando el programa Matlab, calculamos la constante de tiempo del sistema en bucle abierto y en función de ella el tiempo de muestreo para la discretización del proceso.
» ctetpo=1/0.64884
ctetpo = 1.5412
» Ts=ctetpo/10
Ts = 0.1541
Calculamos el equivalente discreto del proceso
» [nd,dd]=c2dm(n,d,Ts,'zoh')
nd = 0 -0.2443
dd = 1.0000 -0.9048
» printsys(nd,dd,'z')
num/den =
-0.24428
-----------
z - 0.90484
Comprobamos la respuesta en bucle abierto del sistema
» dstep(nd,dd)
Al igual que el sistema continuo resulta estable en bucle abierto. Para calcular el rango de estabilidad usamos la misma función rlocus.
» zgrid('new')
» rlocus(nd,dd)
En el lugar de las raíces vemos que el sistema en bucle cerrado será estable en un rango pequeño de K positivas y en un rango algo mayor de K negativas. Para conocer las K's límite escribimos:
» [k,poles]=rlocfind(nd,dd)
Select a point in the graphics window
Sobre el gráfico seleccionamos los puntos (1,0) y (-1,0) como polos de bucle cerrado y la función nos da el valor de las dos K's, una para cada polo.
selected_point = 0.9998 - 0.0002i
k = 0.3887
poles = 0.9998
selected_point = -1.0000 - 0.0058i
k = 7.7978
poles = 2.8097
Por lo tanto el rango de estabilidad es K"[-7.7978, 0.3887]
Con el programa CC, introducimos la función de transferencia en bucle abierto y ejecutamos el comando Routh
CC>dig
Now in digital mode
Enter sample time T > 0.1541
Sample time T = 0.1541 , Rate = 1 / T = 6.489293 , Foldover PI / T = 20.38671
DIG>gdba = -0.24428 / (z - 0.90484)
DIG>routh,gdba
Stable for gain ranges: - 7.797773 to 0.389553
c) Simulación en bucle cerrado
Introducimos en Simulink el siguiente diagrama de bloques:
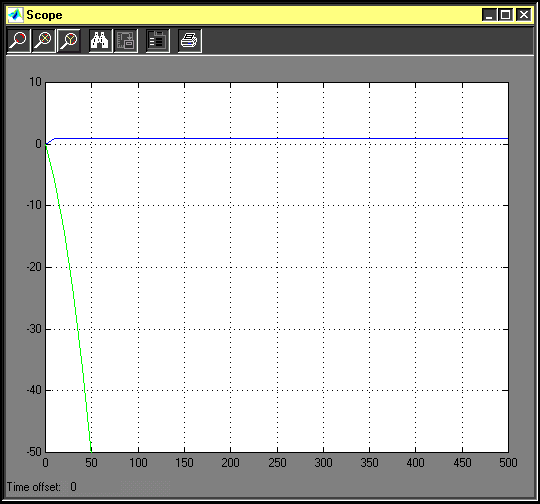
Simulamos el proceso para una k inferior a la crítica (K=0.38) y obtenemos un respuesta estable.
En cambio, para una ganancia superior a la crítica (K=0.4) el sistema se inestabiliza y obtenemos la siguiente gráfica:
EJERCICIO - 2
a) Proceso a controlar
-
Generamos aleatoriamente en Matlab un proceso de segundo orden.
» [n,d]=rmodel(2)
n = 0 0 -0.5883
d = 1.0000 2.7744 14.6867
» printsys(n,d)
num/den =
-0.58832
------------------------
s^2 + 2.7744 s + 14.6867
En forma de polos y ceros obtenemos:
» [z,p,k]=tf2zp(num,den)
z = Empty matrix: 0-by-1
p = -1.3872 + 3.5724i
-1.3872 - 3.5724i
k = -0.5883
-
Para ver la dinámica natural del sistema en bucle abierto, dibujamos su respuesta frente a un escalón unitario. En Matlab, escribimos:
» step(n,d)
Vemos que el sistema es estable en bucle abierto, aunque con ganancia negativa.
b) Diseño del regulador PID por el método directo
-
Obtenemos el periodo de muestreo necesario para discretizar el sistema:
» wn=sqrt(den(3))
wn = 3.8323
» ws=20*wn
ws = 76.6465
» fs=ws/(2*pi)
fs = 12.1987
» Ts=1/fs
Ts = 0.0820
-
Discretizamos el proceso:
» [nd,dd]=c2dm(n,d,Ts,'zoh')
nd = 0 -0.0018 -0.0017
dd = 1.0000 -1.7090 0.7966
» printsys(nd,dd,'z')
nd/dd =
-0.0018202 z - 0.001687
-----------------------
z^2 - 1.709 z + 0.79657
Obtenemos los polos y ceros del sistema discretizado:
» [z,p,k]=tf2zp(nd,dd)
z = -0.9444
p = 0.8545 + 0.2577i
0.8545 - 0.2577i
k = -0.0018
Dibujamos el lugar de las raíces para K negativas ya que el proceso tiene ganancia negativa.
» rlocus(-nd,dd)
-
A continuación obtenemos las especificaciones:
» teba=4/1.3872
teba = 2.8835
» tebc=teba/2
tebc = 1.4418
Por los tanto tomamos un tiempo de establecimiento de un segundo
» tebc=1;
» fi=den(2)/(2*wn)
fi = 0.3620
» deltaba=exp((-fi*pi)/sqrt(1-fi^2))
deltaba = 0.2953
» deltabc=deltaba/2
deltabc = 0.1476
La sobreoscilación de diseño será:
» deltabc=0.1;
Vamos a obtener los polos de bucle cerrado
» sigmabc = 4/tebc
sigmabc = 4
fibc=sqrt(log(deltabc)^2/(log(deltabc)^2+pi^2))
fibc = 0.5912
» wnbc=sigmabc/fibc
wnbc = 6.7664
» wpbc=wnbc*sqrt(1-fibc^2)
wpbc = 5.4575
» p1=-sigmabc+wpbc*i
p1 = -4.0000 + 5.4575i
» p2= -sigmabc-wpbc*i
p2 = -4.0000 - 5.4575i
Discretizamos los polos de bucle cerrado
» z1=exp(p1*Ts)
z1 = 0.6495 + 0.3117i
» z2=exp(p2*Ts)
z2 = 0.6495 - 0.3117i
-
Diseñamos un regulador PID para que el sistema en bucle cerrado cumpla las especificaciones obtenidas. El PID tiene la forma:
Para obtener los parámetros del regulador aplicamos el criterio del argumento:
Resolvemos la ecuación del criterio del argumento:
!
Por lo tanto ![]()
.
Para obtener b procedemos de la siguiente manera:
![]()
siendo d la distancia entre z = 1 y la parte real de las especificaciones.
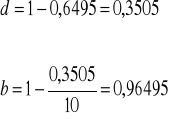
El regulador que resulta sin conocer la K de momento es
Para obtener la ganancia utilizamos el Matlab:
» nr=[1 -1.74065 0.7485117]
nr = 1.0000 -1.7407 0.7485
» dr=[1 -1 0]
dr = 1 -1 0
» printsys(nr,dr,'z')
num/den =
z^2 - 1.7407 z + 0.74851
------------------------
z^2 - 1 z
A continuación obtenemos el valor de k, para que nuestro regulador pase por las especificaciones:
» [nbc,dbc]=series(nr,dr,nd,dd);
» zgrid('new')
» p=[z1;z2]
p = 0.6495 + 0.3117i
0.6495 - 0.3117i
» [k,poles]=rlocfind(nbc,dbc,p);
» k
k = 99.4290 99.4290
Finalmente obtenemos el siguiente regulador:
» [nr,dr]=series(nr,dr,k,1);
» printsys(nr,dr,'z')
num/den =
99.429 z^2 - 173.0711 z + 74.4238
---------------------------------
z^2 - 1 z
Para simular el regulador introducimos el siguiente diagrama de bloques en Simulink:
EJERCICIO - 3
a) Regulador por asignación de polos
Utilizando el programa CC podemos resolver fácilmente el regulador de asignación de polos sin más que introducir el proceso y los polos deseados.
Now in digital mode
Enter sample time T > 0.082
Sample time T = .082, Rate 1/T = 12.19512, Foldover PI/T = 38.31211
DIG>diopole
Diophantine equation pole-placement algorithm
where Input: g=system
Solution: k=compensator
Enter g,k > gd,reg1
System g is order 1 over 2
Compensator k is proper (#poles>=#zeros) if p>= 3
Closed loop system gk/(1+gk) is proper if p>= 2
Enter # closed loop poles (p) > 3
Enter 3 poles
Real poles are entered as a single number
Complex poles are entered as real,imag separated by a comma
1 > 0.6495,0.8117
2 > 0.6495,-0.8117
3 > 0
DIG>pzf,reg1
1.091854(z-.284055)
REG1(z) = ---------------------
(z+.1550732)
Para comprobar su funcionamiento, lo simulamos con Simulink. Introducimos el siguiente diagrama de bloques:
b) Regulador de tiempo mínimo
Utilizamos el programa CC, que nos resuelve directamente el regulador
Program CC, Version 4
(C) Copyright Peter M. Thompson, 1984-1991.
Uses Microsoft QuickBasic Compiler, Version 6.00
(C) Copyright Microsoft Corp. 1982-1988.
HELP = list of commands
C>a=0.0018213
C>b=(z-1)
C>phi=z
DIG>dig,0.082
Sample time T = .082, Rate 1/T = 12.19512, Foldover PI/T = 38.31211
IG>diophantine
Diophantine polynomial equation: a*x + b*y = phi
No solution found if a&b have common factors.
If m>0 and n>0 then order(x)=n-1 and order(y)=max[p-n,m-1].
where Input: a = polynomial, order = m
Input: b = polynomial, order = n
Input: phi = polynomial, order = p
Solution: x = polynomial
Solution: y = polynomial
Enter a,b,phi,x,y >
Enter a,b,phi,x,y > a,b,phi,x,y
DIG>reg2=x*(z^2-1.709*z+0.79657)/(y*(z-1)*(z+0.9268213)
Mismatched parentheses
DIG>reg2=x*(z^2-1.709*z+0.79657)/(y*(z-1)*(z+0.9268213))
DIG>pzf,reg2
-549.0583[(z-.8545)^2+.2576815^2]
REG2(z) = ----------------------------------
(z+.9268213)(z-1)
Para comprobar su funcionamiento, lo simulamos con Simulink. Introducimos el siguiente diagrama de bloques:
Y la respuesta del sistema la podemos observar en la siguiente gráfica:
c) Regulador de tiempo finito
Para diseñarlo utilizamos el mismo comando de CC, que lo resuelve directamente
DIG>a=(-0.008181231*(z+0.9268))
DIG>b=(z-1)
DIG>phi=z
DIG>diophantine
Diophantine polynomial equation: a*x + b*y = phi
No solution found if a&b have common factors.
If m>0 and n>0 then order(x)=n-1 and order(y)=max[p-n,m-1].
where Input: a = polynomial, order = m
Input: b = polynomial, order = n
Input: phi = polynomial, order = p
Solution: x = polynomial
Solution: y = polynomial
Enter a,b,phi,x,y > a,b,phi,x,y
DIG>reg3=(x*(z^2-1.709*z+0.79657))/(y*(z-1))
DIG>pzf,reg3
-286.37[(z-.8545)^2+.2576815^2]
REG3(z) = ---------------------------------
(z-1)(z+0.481)
EJERCICIO - 4
La función de transferencia que modela el proceso es:
La función de transferencia que modela la perturbación es:
a) Diseño del regulador de mínima varianza MV4
El regulador de mínima varianza (MV4) tiene la siguiente estructura:
Sustituyendo los polinomios, obtenemos:
Para observar la respuesta del sistema usando el regulador MV4, utilizamos el simulink de Matlab. Simulamos a la vez un regulador proporcional de ganancia unitaria.
El diagrama de bloques que introducimos en Matlab se muestra a continuación:
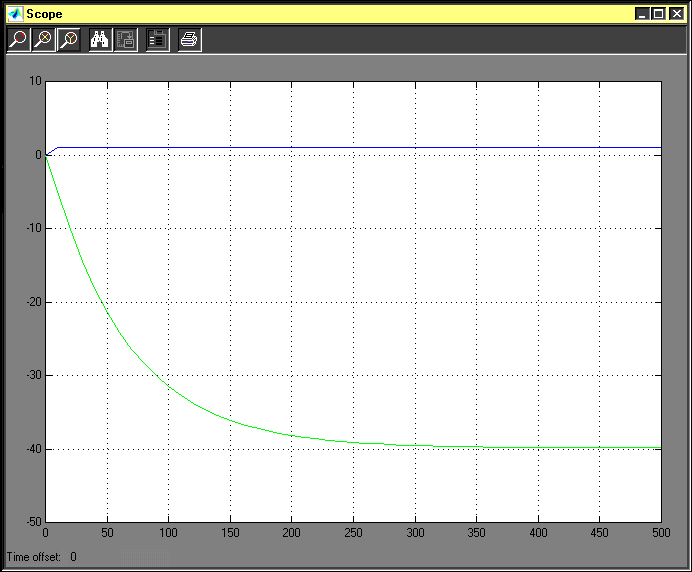
El resultado de la simulación se muestra en la siguiente gráfica:
En color verde aparece el escalón de entrada. La respuesta del sistema con regulador de mínima varianza MV4 es la de color rojo y azul es la del regulador proporcional de ganancia unidad.
Se observa cómo el MV4 reduce enormemente la varianza de la salida en comparación con el proporcional a la vez que consigue un transitorio muy rápido y sin excesiva sobreoscilación y un menor error de posición.
b) Diseño del regulador de mínima varianza MV3 con limitación de la acción de control
El regulador de mínima varianza (MV3) tiene la siguiente estructura:
Para limitar la acción de control al 50% del MV4, debemos hacer y entonces
c) Regulador PI para el MV3
El regulador de mínima varianza MV3 no consigue eliminar el error de posición. Para eliminarlo colocamos un PI detrás del MV3. La estructura del PI es la siguiente:
Para ajustar los parámetros del regulador debemos estudiar el sistema que tenemos hasta el momento. El ajuste lo realizaremos para que el PI elimine el error de posición pero afectando mínimamente a la respuesta conseguida por el MV3.
A efectos de diseño podemos considerar el MV3 y el proceso como una única función de transferencia. Para obtenerla utilizamos el Matlab. Introducimos el regulador:
» nmv=[0.709 -0.5566]
nmv = 0.7090 -0.5566
» dmv=[-0.0036 +0.0001 -0.000432]
dmv = -0.0036 0.0001 -0.0004
Introducimos el proceso:
» np=[-0.0018 -0.0017]
np = -0.0018 -0.0017
» dp=[1 -1.709 +0.7966]
dp = 1.0000 -1.7090 0.7966
Y el proceso resultante de poner ambas funciones de transferencia en serie, será:
» [n,d]=series(nmv,dmv,np,dp)
n = 0 0 -0.0013 -0.0002 0.0009
d = -0.0036 0.0063 -0.0035 0.0008 -0.0003
» printsys(n,d,'z')
num/den =
-0.0012762 z^2 - 0.00020342 z + 0.00094622
--------------------------------------------------------------------------------------------
-0.0036 z^4 + 0.0062524 z^3 - 0.0034707 z^2 + 0.00081795 z - 0.00034413
La función de transferencia de bucle cerrado será la siguiente:
» x=n+d
x = -0.0036 0.0063 -0.0047 0.0006 0.0006
» printsys(n,x)
num/den =
-0.0012762 s^2 - 0.00020342 s + 0.00094622
-----------------------------------------------------------------------
-0.0036 s^4 + 0.0062524 s^3 - 0.0047469 s^2 + 0.00061453 s + 0.00060209
Obtenemos sus polos:
» [z,p,k]=tf2zp(n,x)
z = -0.9444
0.7850
p = 0.6517 + 0.7129i
0.6517 - 0.7129i
0.6923
-0.2589
k = 0.3545
Por tanto el polo dominante de bucle cerrado (antes de incluir el PI) será 0.6923.
Ajustamos el cero del PI para que no afecte a la dinámica conseguida por el regulador de mínima varianza. Si definimos d como la distancia entre el integrador (z = 1) y el polo dominante de bucle cerrado (z = 0.6923), tendremos que d = 0.3077.
Entonces, el cero b se calcula de la siguiente forma:
Y a la ganancia K le asignamos un valor unitario para que no afecte a la regulación de mínima varianza.
El regulador que resulta es:
d) Comparación de los reguladores mediante la varianza de la salida
A continuación se muestra el diagrama de bloques que introducimos en Simulink, para simular a la vez los cuatro reguladores estudiados: P, MV4, MV3 y MV3 + PI.
La siguiente gráfica muestra los resultados de la simulación. Las señales son:
Negra: escalón de entrada.
Azul marino: respuesta del regulador P de ganancia unitaria.
Rojo: respuesta del regulador MV4.
Azul celeste: respuesta del regulador MV3.
Rosa: respuesta del regulador MV3 + PI.
Como era de esperar podemos observar lo siguiente:
-
El regulador proporcional no elimina el ruido de la salida y no consigue que el sistema siga la referencia. Tiene la mayor varianza de los cuatro.
-
El regulador MV4 es el que consigue la mínima varianza en la salida, pues al no tener limitada la acción de control responde antes a las perturbaciones. Tiene error de posición, pues es algo que no se controla en este tipo de reguladores.
-
El regulador MV3 es idéntico al MV4 pero con limitación en la acción de control. Debido a esto no consigue controlar la varianza de la salida tan bien como el MV4. Su error de posición y su transitorio son similares al MV3.
-
Por último, si añadimos al MV3 un PI obtenemos una respuesta con la misma varianza que el MV3 pero sin error de posición.
1
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()


![]()

![]()
![]()
![]()


![]()
![]()






![]()
![]()
Descargar
| Enviado por: | Usuario Invitado |
| Idioma: | castellano |
| País: | España |
