Matemáticas
Geometría analítica
INTEGRANTES
5TO COMPUTACIÓN
SECCIÓN A:
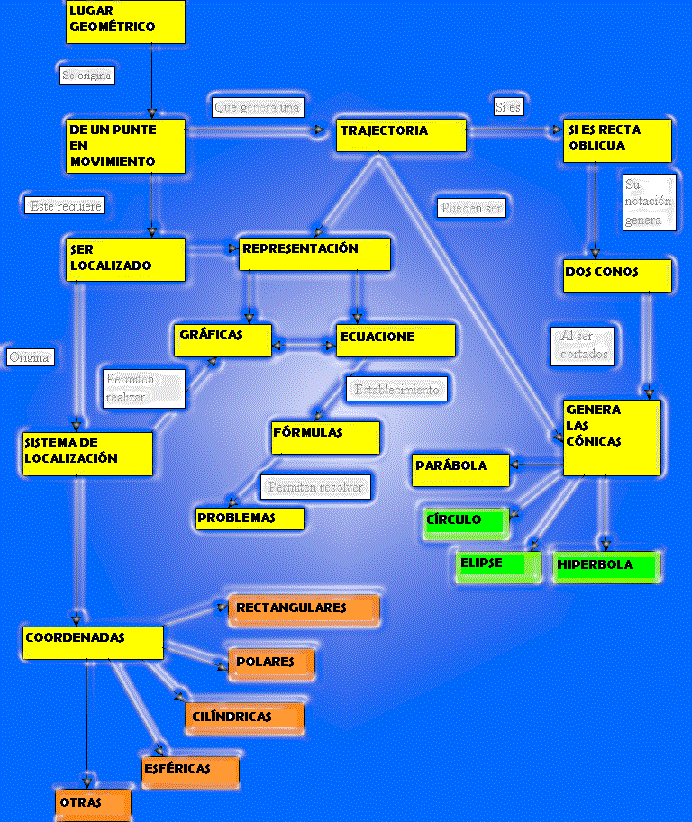
MAPA CONCEPTUAL DE LA GEOMETRIA ANALITICA
GEOMETRIA ANALITICA

La Geometría Analítica tiene por objeto la resolución de problemas geométricos utilizando métodos algebraicos. El sistema que se emplea para representar gráficas fue ideado por el filósofo y matemático francés Descartes (1.596 -1.650), quien usó su nombre latinizado, Renatus Cartesius, y por esta razón se conoce con el nombre de ejes cartesianos.
OBJETIVOS:
-
Identificar las coordenadas de un punto en el plano y conocer su interpretación geométrica.
-
Reconocer y representar gráficamente lugares geométricos de puntos a distancia constante de los ejes.
-
Expresar en una tabla de valores y representar gráficamente las soluciones de una ecuación de primer grado con dos incógnitas.
-
Estudiar analíticamente la incidencia entre puntos y rectas.
-
Determinar la posición relativa entre dos rectas y, como aplicación, discutir y resolver un sistema 2x2.
En la Geometría Analítica se estudian las figuras geométricas planas introduciendo un sistema coordenado, de tal manera de que dada una ecuación se determina su gráfica y recíprocamente, dada una gráfica, deducir su ecuación.
ESPACIO VECTORIAL.
Es un conjunto arbitrario diferente del vacío en el cual se han definido dos operaciones: adición y producto por un número. Un conjunto es una colección de objetos que está bien definida, por definida, entendemos que siempre es posible saber si un elemento o no pertenece a una colección o conjunto.
Algunos ejemplos de espacios vectoriales son:
Con las operaciones usuales los siguientes conjuntos se constituyen como espacios vectoriales: Matrices de n×n ; P(n) (polinomios), funciones continuas, IRn (producto cartesiano). Por ahora consideraremos el conjunto IR2 = { (x, y) | ... } y veremos las siguientes operaciones:
Sea un vector ^u = (x1, y1) y ^v = (x2, y2) y k un escalar entonces definimos las siguientes operaciones:
^u + ^v = (x1 + x2, y1 + y2) k^u = (kx1, ky1) ^u ·^v = x1 · x2 + y1 · y2
Y además se satisfacen los siguientes axiomas:
Sean vectores denotados como ^u, ^v y ^w y a, b, c escalares, entonces:
^u + ^v = ^v + ^u
(^u + ^v )+ ^w = ^u + (^v + ^w)
^u + 0 = 0 + ^u = ^u
^u + ( - ^u) = 0
a(b^u) = (ab)^u = ^u(ab)
a(^u + ^v) = a^u + a^v
(a + b)^u = a^u + b^v
1^u = ^u
^u·^v = ^v·^u
^u(^v + ^w) = ^u·^v + ^u·^w
c(^u^v) = (c^u)^v = ^u(c^v)
En IR² ó IR³ cuando consideramos un punto (x, y) cualquiera y lo representamos gráficamente en el plano cartesiano trazando una línea de leal origen, recibe el nombre de vector de posición o vector anclado. Además, si el vector ^u es elemento de IR², entonces ^u = (x, y).
En la siguiente gráfica ^u es un vector anclado, observemos los demás elementos que componen dicha gráfica:
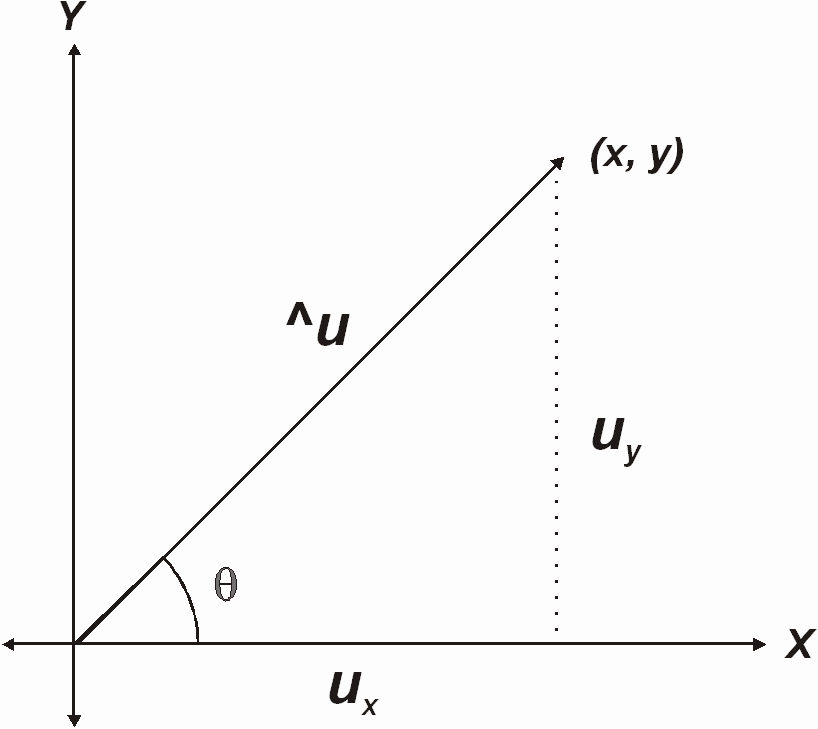
Podemos observar que:
^u = ux + uy donde ux = (x, 0) y uy = (y, 0)
Denotamos como || ^u || a la distancia del origen al punto (x, y) denominada magnitud del vector ^u y de donde obtenemos las siguientes conclusiones:
-
|| ^u || = (x² + y²)½
-
Cos(ð) = x / || ^u ||
-
Sen(ð) = y / || ^u ||
-
Para un vector anclado ^u, ^ux representa su componente en la dirección x y ^uy representa su componente en la dirección y.
-
La dirección de un vector de posición está dada por el ángulo que forma con el sentido positivo del eje X.
LA LÍNEA RECTA.
Éste concepto matemático parece no tener definición ya que es una sucesión de puntos y éstos carecen de magnitud, pero se considera como una trayectoria de puntos que no cambian de dirección, o bien, en términos del espacio, es la intersección de dos planos. Además tenemos los siguientes conceptos:
-
Segmento de recta: Recta delimitada por dos puntos, ésta es una magnitud lineal finita.
-
Semirrecta: Si se tiene una recta con un punto P contenido en ella y que la divide, cada una de las porciones en que queda dividida se le conoce como semirrecta.
-
Rayo: Se le conoce como la semirrecta en un sentido, simbolizada como
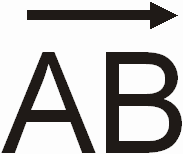
donde la flecha indica el sentido, el origen es A y el destino B, o bien por "r" con una flecha indicando el destino.
Pendiente de una recta.
Uno de los elementos más importantes de la línea recta es la pendiente, la cual se define como la tangente del ángulo de inclinación. El ángulo de inclinación es aquel que forma la recta con el eje positivo de las X. Dados dos puntos por los cuales pasa la recta, su pendiente se calcula así:
-
m = (y2 - y1) / (x2 - x1)
-
m = Tg ().
-
Tg() = y2 / x2 = y1 / x1
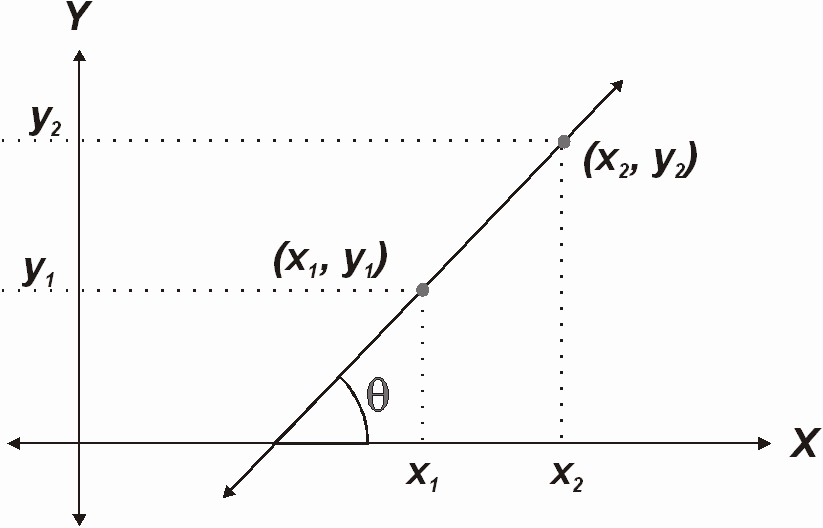
Ecuación de la recta.
-
Forma intercepto-pendiente: y = mx + b (b es el intercepto con el eje Y).
-
Conocidos la pendiente y un punto cualquiera (x1, y1), la ecuación es: y - y1 = m(x - x1).
-
Conocidos dos puntos la ecuación es: y - y1 = [ (y2 - y1) / (x2 - x1) ] · (x - x1)
-
Forma general de la ecuación de la recta: La encontramos haciendo operaciones con cualquiera de las formas antes mencionadas, su representación es: ax + by + c = 0.
Definiciones.
-
Se dice que dos puntos son colineales si están sobre la misma recta.
-
Se dice que dos rectas son perpendiculares si el producto de sus pendientes es -1.
-
Se dice que dos rectas son paralelas si ambas tienen la misma pendiente.
-
La distancia del punto P(x1, y1) a la recta L: Ax + By + C = 0 es: d(P, L) = |Ax1 + By1 + C| / (A² + B²)½
Forma simétrica de la ecuación de la recta.
x/a + y / b = 1 Donde a es el intercepto con x y b el intercepto con y.
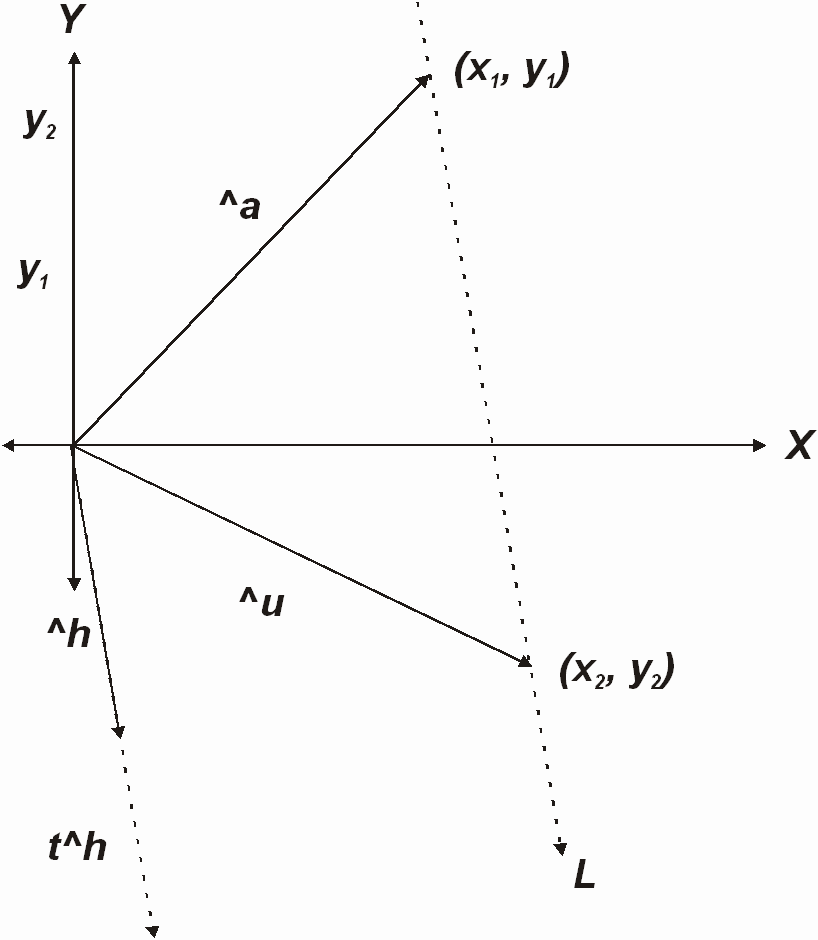
Rectas y vectores.
En el plano cartesiano las rectas y los vectores se relacionan de la siguiente forma: Dados dos puntos (x1, y1) y (x2, y2), entonces, ellos determinan una recta, justamente la que pasa por ambos, y su ecuación se encuentra de forma usual. Vistos los puntos como vectores ^a = (x1, y1) y ^u = (x2, y2), puede plantearse la siguiente pregunta: ¿Cuál es la recta que pasa por la punta del vector ^a en la dirección del vector ^u? (recta L), con mayor precisión, observe en la figura que ^u = ^a + t^h que es la ecuación en forma vectorial de la recta L. Entonces podemos hacer las siguientes sustituciones:
^a + t^h = (x1 + tx2, y1 + ty2) ð x = x1 + tx2 y y = y1 + ty2 y podemos sustituir y despejar t para encontrar la ecuación de la recta en su forma general.
Teorema:
La forma normal de la ecuación de una recta está dada por: xCos(ð) + ySen(ð) - p; donde p es un número positivo numéricamente igual a la longitud de la normal trazada desde el origen a la recta y ð es el ángulo positivo menor a 360°.
CIRCUNFERENCIA.
Circunferencia es el lugar geométrico de un punto que se mueve en el plano de tal manera que se conserva siempre a una distancia constante de un punto fijo de ese plano; el punto fijo se llama centro y la distancia constante radio.
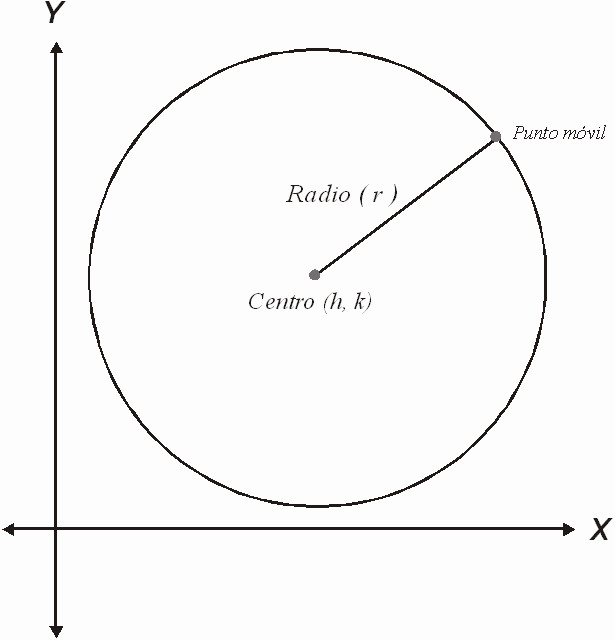
La circunferencia cuyo centro es (h, k) y de radio r tiene por ecuación: (x - h)2 + (y - k)2 = r2 y recibe el nombre de ecuación en forma ordinaria.
Forma general de la ecuación de una circunferencia.
Dada la forma ordinaria (x - h)2 + (y - k)2 = r2 desarrollamos los cuadrados y tenemos:
X2 - 2hx + h2 + y2 - 2ky + k2 = r2; agrupando términos:
X2 + y2 + (-2h)x + (-2k)y + (h2 + k2 - r2) = 0; por último tenemos:
D E F
X2 + y2 + Dx +Ey + F = 0 que es la forma general que buscábamos. De aquí deducimos que cualquier ecuación en forma ordinaria puede transformarse mediante operaciones correctas a la forma general.
Tangente a una circunferencia.
Dada la ecuación de la circunferencia en forma ordinaria o general, hallar la ecuación de la tangente a la circunferencia que tiene dicha ecuación dados un punto de contacto, la pendiente de la de la recta buscada o un punto exterior por el cual pasa la recta tangente.
En geometría elemental se estudia únicamente la tangente a una curva: la circunferencia, el estudio hecho es insuficiente para las curvas planas en general, por ello, estudiaremos un método que se aplique a todas las curvas existentes en el siguiente apartado.
TANGENTE A UNA CURVA.
Dada la función f(x, y) <1> y la recta, que es tangente a esa curva, y = mx + b despejamos y en la ecuación de la recta y la sustituimos en f(x, y), después de esto nos debe quedar una ecuación de segundo grado, la cual hay que resolver con la siguiente condición: sabemos que la ecuación de segundo grado tiene un discriminante, en nuestro caso le llamaremos ð y lo igualaremos a cero quedando de la forma ð = 0 y le llamaremos "condición de tangencia".
En la expresión <1> hablamos de una función general en dos variables y nos referimos a funciones cuadráticas donde y = mx + b representa una familia de rectas y el sistema pretende determinar cuál de esas rectas es tangente.
Resolviendo nos queda una ecuación de segundo grado, como lo habíamos dicho con anterioridad, para la variable x y como estamos buscando una única solución se deduce que el discriminante tiene que ser igual a cero, es decir, estamos hablando de la condición de tangencia.
De manera práctica se encuentran tres casos de tangentes a cónicas.
Se conoce el punto de contacto, aquí hay una sola tangente.
Se conoce la pendiente, aquí hay dos tangentes.
Se conoce un punto exterior por el cual pasa la tangente, aquí hay dos tangentes.
Para hallar las ecuaciones de las tangentes se sustituye el dato conocido en la ecuación de la recta y se resuelve la aplicando la condición de tangencia, determinando así la ecuación de las rectas.
PARÁBOLA.
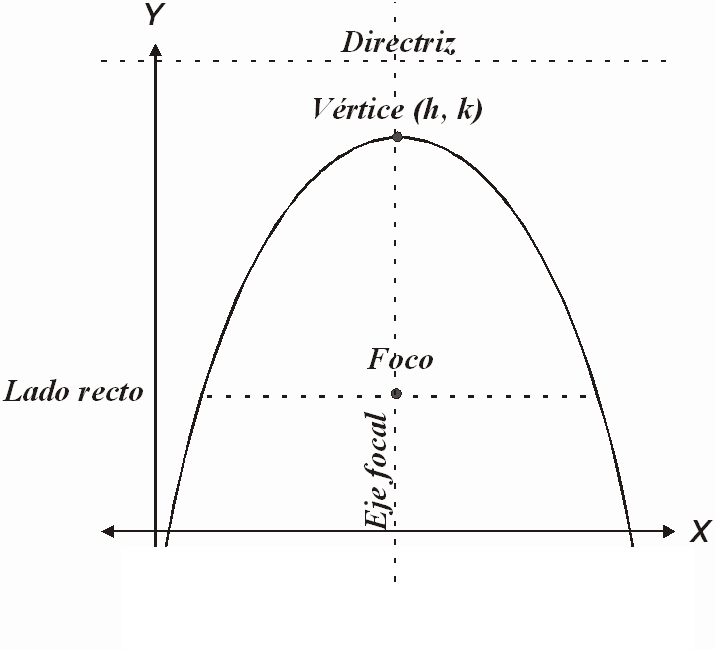
Una parábola es el lugar geométrico de un punto que se mueve en el plano de talo manera que su distancia de una recta fija situada en el plano es siempre igual a su distancia de un punto fijo del plano y que no pertenece a la recta. Al punto fijo se le llama foco y la recta fija directriz.
La recta que es perpendicular a la directriz y que pasa por el foco se llama eje focal, la intersección de la parábola con el eje focal se denomina vértice. La cuerda focal es el segmento de recta perpendicular al eje focal y que pasa por el foco, en nuestra gráfica, esta es el lado recto.
Los elementos de una parábola son entonces: vértice, foco, longitud del lado recto, y la ecuación de la directriz. Nosotros estudiaremos únicamente las parábolas con ejes focales paralelos al eje X o al eje Y. La distancia del vértice a la directriz es la misma distancia del vértice al foco.
Teorema:
La ecuación de una parábola de vértice (h, k) y eje focal paralelo al eje X es de la forma: (y - k)² = 4p(x - h) y sus elementos son los siguientes:
-
Foco(h + p, k)
-
Directriz x = h - p
-
Eje focal y = k
-
Donde 4| p | es la magnitud del lado recto y siendo | p | la longitud entre el foco y el vértice.
-
Si p > 0 la parábola se abre hacia la derecha.
-
Si p < 0 la parábola se abre hacia la izquierda.
Si el eje es paralelo al eje Y la ecuación es de la forma (x - h)² = 4p(y - k) y sus elementos son:
-
Foco (h, k + p)
-
Directriz y = k - p
-
Eje focal x = h
-
Si p > 0 la parábola se abre hacia arriba.
-
Si p < 0 la parábola se abre hacia abajo.
ELIPSE.
Una elipse es el lugar geométrico de un punto que se mueve en el plano de tal manera que las sumas de sus distancias a dos puntos fijos de ese plano es siempre igual a una constante mayor que la distancia entre los dos puntos. Los dos puntos fijos se llaman focos de la elipse.
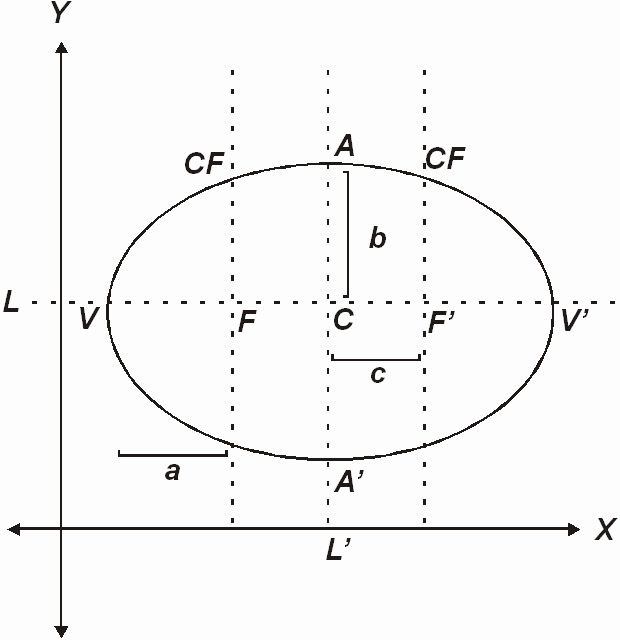
Los elementos de una elipse son los que se describen en la figura siguiente:
-
F y F', focos.
-
V y V', vértices
-
C, centro.
-
d(V, V'), eje mayor.
-
CF, lado recto.
-
d(A, A') eje menor.
-
L', eje normal.
-
L, eje focal.
Es importante observar que F, F', C, V y V' tienen una coordenada en común y que la distancia de F a V es igual a la distancia de F' a V' y que C es el punto medio de los focos y vértices.
Teorema:
La ecuación de una elipse con C(h, k) y eje focal paralelo al eje X esta dada por: (x - h)² / a² + (y - k)² / b² = 1, y paralela al eje Y es: (x - h)² / b² + (y - k)² / a² = 1.
En donde para cada elipse, a es la longitud del semieje mayor, b es la del semieje menor, c es la distancia del centro hacia cada foco y a, b, c están ligadas por la siguiente relación: a² = b² + c².
También para cada elipse, la longitud de cada uno de sus lados rectos es: 2b² / a y la excentricidad e = c / a.
HIPÉRBOLA.
Una hipérbola es el lugar geométrico de un punto que se mueve en el plano de tal manera que el valor absoluto de la diferencia de sus distancias a dos puntos fijos del plano, llamados focos, es igual a una constante positiva y menor que la distancia entre los focos. Sus elementos son los que se muestran en la figura:
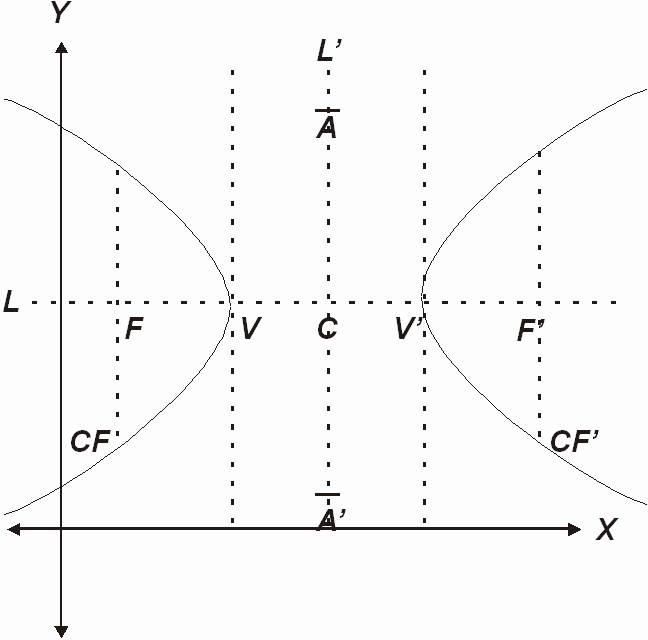
-
F y F', focos.
-
V y V', vértices.
-
L, eje focal.
-
VV', eje transverso.
-
C, centro.
-
L', eje normal.
-
AA', eje conjugado.
-
CF, lado recto.
Teorema:
La ecuación de una hipérbola con centro en el punto C(h, k), y eje focal paralelo al eje X es de la forma:
(x - h)² / a² - (y - k)² / b² =1, sus focos son (h + c, k) y (h .- c, k) y sus vértices son (h - a, k) y (h + a, k).
Si el eje focal es paralelo al eje Y su ecuación es de la forma: (y - k)² / a² - (x - h)² / b² = 1, sus focos son (h , k + c) y (h, k - c) y sus vértices son (h - a, k ) y (h + a, k ).
Donde para cada parábola a es la longitud del semieje transverso, b la del semieje conjugado y c la distancia del centro a cada foco; a, b, c están ligadas por la relación c² = a² + b².. También la longitud de cada lado recto es 2b² / a y la excentricidad está dada por la relación e = c /a..
ASÍNTOTAS.
Si para una curva dada, existe una recta talque, a medida que un punto de la curva se aleja indefinidamente del origen, la distancia de ese punto a esa recta decrece continuamente y tiende a cero dicha curva se llama asíntota de la curva, la cual puede ser horizontal o vertical.
Teorema:
La hipérbola b²x² - a²y² = a²b² tiene por asíntotas las rectas: bx - ay = 0 y bx + ay = 0.
SUBTANGENTE Y SUBNORMAL.
Veamos la siguiente figura:

siguiendo la figura podemos decir lo siguiente:
-
L es tangente a la curva C en el punto P1.
-
L' es la recta trazada por P1 perpendicular a L y se llama normal a C en P1. Su ecuación es y - y1 = -1/m(x - x1).
-
La tangente y la normal cortan al eje X en T y N.
-
La longitud P1T es la longitud de la tangente y P1N es la longitud de la normal.
-
La proyección QT de la longitud de la tangente sobre X se llama subtangente .
-
La proyección QN de la longitud de la normal sobre X se llama subnormal.
Si m es la pendiente de una curva plana continua C en P1(x2, y1), entonces en P1 tenemos:
-
Ecuación de la tangente a C: y - y1 = m(x - x1).
-
Ecuación de la normal a C: y - y1 = -1/m(x - x1) con m != 0.
-
Longitud de la tangente: y1 / m (1 + m²) ½ con m ¡= 0.
-
Longitud de la normal: y1(1 + m²)½ .
-
Longitud de la subtangente: y1 / m
-
Longitud de la subnormal: my1.
ECUACIÓN GENERAL DE SEGUNDO GRADO.
Esta ecuación tiene la siguiente forma: Ax² + Bxy + Cy² + Dx + Ey + F = 0 y representa alguna de las cónicas.
Teorema:
La ecuación general de segundo grado representa una cónica del género parábola, elipse o hipérbola según el indicador I = B² - 4AC sea 0, negativo o positivo respectivamente.
TRANSFORMACIÓN DE COORDENADAS.
Una transformación es una operación por la cual una relación, expresión o figura se cambia por otra siguiendo una ley dada. Analíticamente la ley se expresa mediante una o más ecuaciones llamadas "ecuaciones de transformación".
Traslación de ejes de coordenadas.
Si se trasladan los ejes coordenados a un nuevo origen, O' es el punto (h, k), y si las coordenadas de cualquier punto antes y después de la traslación son (x, y) y (x', y') respectivamente, las ecuaciones de transformación del sistema primitivo al nuevo sistema de coordenadas son:
x = x' + h; x' = x - h
y = y' + k; y' = y - k
Rotación de ejes de coordenadas.
Si los ejes coordenados giran un ángulo ð en torno de su origen como centro de rotación y las coordenadas de un punto cualquiera P antes y después de la rotación son (x, y) y (x', y') respectivamente, las ecuaciones de transformación del sistema original al nuevo sistema están dadas por:
x = x'cos(ð) - y'sen(ð); y = x'sen(ð) + y'cos(ð)
COORDENADAS POLARES.
Veamos la siguiente gráfica:

De ella podemos decir que x = rCos(ð) y y = rSen(ð), por tanto, podemos representar el punto P(x, y)mediante otro sistema denominado coordenadas polares que toma en cuenta la magnitud r y el ángulo ð, así, el punto P(x, y) lo podemos escribir como P(r, ð).
LUGAR GEOMÉTRICO.
El ligar geométrico lo podemos definir como el conjunto de puntos y solo de aquellos puntos cuyas coordenadas satisfacen la ecuación f(x, y)=0, y además, cualquier punto que se mueve en el plano describe una curva. El hallar la ecuación de la curva y todas sus propiedades es un problema de lugar geométrico, donde se busca una expresión matemática que describa la situación.
Lugar geométrico de la recta en 3 dimensiones.
Dados dos puntos fijos la recta se describe por aquellos puntos que se mueven a lo largo del vector que describen esos dos puntos en dirección contraria.
Ecuaciones paramétricas.
La recta queda determinada por un punto fijo P0 y un vector ^v = a^i + b^j + c^k, el conjunto de los puntos P, tales que PoP es paralelo a ^v, es decir, que satisfacen d(P0, P) = t^v para algún número real t.
Si r = OP y r0 = OP son los vectores de posición de P y P0, respectivamente, entonces:
ð P0P = t^v
ð P0P = r - r0
ð r = r0 + t^v (1)
Si escribimos r = (x, y ,z) y r0 = (x0, y0. z0) e igualamos los componentes en (1) tenemos,
x = x0 + at; y = y0 + bt ; z = z0 + ct
y éstas se denominan ecuaciones paramétricas (vea la gráfica).

Si despejamos t de las ecuaciones paramétricas obtenemos las ecuaciones simétricas o estándar:
(X - x0) / a = (y - y0) / b = (z - z0) / c
DISTANCIA DE UN PUNTO A UNA RECTA.
Para hallar la distancia de un punto P(r, s) a una recta dada tenemos dos alternativas, calcularla mediante:
P(r, s) Recta L: Ax + By + C = 0
d(P, L) = + Ar + Bs + C / (A² + B²)½ (1)
y otra alternativa es calcularla de forma vectorial la cual está dada por:
d(P, L) = | ^L × ^K | / | ^L |, donde K y L son vectores determinados, aquí el procedimiento que se sigue es obtener los vectores K y L, realizar el producto vectorial por medio de determinantes y llegar a la fórmula (1).
EL PLANO.
Primero definamos lo que es producto cruz, sean vectores ^v = (x1, x2, x3 ) y ^w = (y1, y2, y3), entonces lo definimos por medio del cálculo del determinante siguiente:

el cual también es un elemento de IR³.
Ahora sí definimos al plano, un plano en tres dimensiones es el lugar geométrico de los puntos, por los que u punto móvil se traslada de tal forma que el vector de él a un punto fijo de él es siempre perpendicular a un vector fijo llamado normal al plano. Consideremos la ecuación del plano como Ax + By + Cz + D = 0 con A, B, C no todas nulas.
Para dos vectores dados cualesquiera ^v y ^w su producto cruz (^v × ^w) es un vector perpendicular a ^v y a ^w y sus números directores son los mismos que los de la normal al plano.
LA ESFERA.
El lugar geométrico de una esfera, es el lugar de un punto en el espacio que se mueve de tal manera que su distancia a un punto fijo es siempre constante. El punto fijo se llama centro y la distancia radio. Su ecuación es muy parecida a la de la circunferencia, esta es: (x - a)² + (y - b)² + (z - c)² = r², donde r es el radio y (a, b, c) es el centro del cual hablamos. En el caso de la circunferencia hablamos de recta tangente, pero en el caso de la esfera hablaremos del plano tangente a una esfera, el cual se obtiene buscando el vector que describe el centro con el punto de contacto y determinar la ecuación de la normal al plano.
La forma general de la ecuación de la esfera es : x² + y² +z² + Gx + Hy + Iz + K = 0
Coordenadas esféricas.
Es posible representar un punto en el espacio en otro sistema de coordenadas denominado coordenadas esféricas, el cual considera la distancia al origen y los ángulos que forma ese radio vector con los ejes X y Z, eto implica que el punto P(x, y, z) puede escribirse como: P(r, ð, ð).
Teorema:
Las coordenadas rectangulares y esféricas de un punto en el espacio están ligadas por las relaciones:
X = rSen(ð)Cos(ð); y = rSen(ð)Sen(ð); z = rCos(ð).
SUPERFICIES.
Se llama superficie al conjunto de puntos cuyas coordenadas satisfacen una ecuación del tipo f(x, y, z) = 0.
Definición:
Se dice que dos puntos distintos son simétricos con respecto a un plano si y solamente si el plano es perpendicular al segmento que los une en el punto medio.
Definición:
Se dice que una superficie es simétrica con respecto a un plano de simetría δ si el simétrico de cada punto de la superficie respecto del plano δ es también un punto de la superficie.
Construcción de una superficie.
Construir una superficie es muy complicado, por ello se han diseñado otras estrategias para hacer la tarea más fácil, lo cual contempla seguir los siguientes puntos en la construcción de cualquier superficie:
Verificar los interceptos con los ejes coordenados:
En las intercepciones con los ejes, los puntos tienen la forma en el plano X (x, 0, 0) en el plano Y(0, y, 0) en el plano Z(0, 0, z), que como pertenecen a la ecuación de la superficie, satisfacen la misma, y al hacerlo, podemos encontraren valor de x, y y z.
Verificar las trazas:
Un razonamiento similar al de los interceptos nos lleva a encontrar las trazas de la superficie, que son las figuras que forma esa superficie cuando se intercepta con alguno de los ejes coordenados, entonces aquí buscamos ecuaciones sencillas. Los puntos de las trazas en los planos correspondientes tienen la siguiente expresión: en el plano XY(x, y, 0) en el plano XZ(x, 0, z) y en el plano YZ(0, y, z), que como pertenecen también a la superficie, deben satisfacer su ecuación, por lo que al sustituir cada uno de esto puntos en la ecuación de la superficie se determina la curva correspondiente (la ecuación) de la traza en sus planos respectivos.
Verificar la simetría de la superficie.
Para verificar la simetría de una superficie nos ayudamos de la siguiente tabla que dice:
| Tabla de simetría | |
| Si la ecuación de la superficie no se altera cuando las variables x, y y z son reemplazadas por: | La superficie es simétrica respecto al: |
| -x, y, z | Plano YZ |
| x, -y, z | Plano XZ |
| x, y, -z | Plano XY |
| -x, -y, z | Eje Z |
| -x, y, -z | Eje Y |
| x, -y, -z | Eje X |
| -x, -y, -z | Origen |
Verificar secciones.
Para hacerlo, se trazan planos paralelos a la superficie para observar que curva se forma cuando se interceptan. Ahora los puntos toman la forma: en el plano XY(x, y, k), k = z, en el plano XZ(x, k, z), k = y y en el plano YZ(k, y, z), k = x.
Definir la extensión de la superficie.
Simplemente se refiere al alcance que tiene la superficie, es decir, cuales son sus límites, si está definida dentro de un intervalo de valores para las variables o no, etcétera.
TEMA DE APLICACIÓN.
Construcción de volúmenes.
Por volumen entendemos una porción del espacio limitada por una o más superficies, si un volumen está limita solo por una superficie, tal como un elipsoide, dicho volumen puede representarse mediante la construcción de una superficie, si un volumen está limitado por una o más superficies, su construcción requiere la construcción de cada superficie que lo forma y de sus curvas de intersección, veamos dos ejemplos:
EJEMPLO 1: Construir el volumen limitado por las superficies x² + y² = 4 y x + y - z = 0.
Solución: La superficie que se desea está limitada por la superficie del cilindro circular recto x² + y² = 4, el plano x + y - z = 0 y los planos coordenados x = 0, y = 0, y z = 0. Construimos primero una parte del cilindro en el primer octante. El plano x + y - z = 0 pasa por el origen y se puede construir mediante sus trazas sobre los planos XZ y YZ. Luego construimos la curva de intersección de este plano y el cilindro; para obtener cualquier punto P de esta curva, empleando un plano de corte paralelo al plano XZ, lo hacemos como indica la siguiente figura, el contorno del volumen aparece en la línea llena.

EJEMPLO 2: Construir el volumen limitado por la superficie x² + 2y = 4, 2y = 3z , x - y + 1 = 0, x = 0 y z = 0 y que está a la izquierda del plano x - y + 1 = 0.
Solución: La porción de la curva de intersección del cilindro parabólico recto x² + 2y = 4 y el plano 2y = 3z aparece en la última figura por el arco AB. El plano x - y + 1 = 0 corta al arco AB en el punto D, al cilindro en la generatriz CD, al plano 2y = 3z en la recta DE y al eje Y en el punto F , entonces el volumen requerido, que aparece en la línea gruesa, está limitado por las porciones ACD del cilindro. AOED del plano 2y = 3z, CDEF del plano x - y + 1 = 0, OEF del plano x = 0 y AOFC del plano z = 0.

Descargar
| Enviado por: | Mynor Gonzalez |
| Idioma: | castellano |
| País: | Guatemala |
