Fundamentos matemáticos de la electrónica digital

Sistemas de numeración posicionales: decimal, binario, octal y hexadecimal. Conversión de un sistema a otro. Operaciones con números binarios. Suma modulo dos.

Códigos. Códigos binarios, continuos. Código de Gray. Códigos alfanuméricos. ASCII. Códigos BCD: distintos tipos. Códigos detectores y correctores de errores. Códigos de paridad y de Hamming.

Representación de los números binarios signados según las convenciones de signo y magnitud. Complemento a uno y a dos. Suma y resta de magnitudes binarias y números binarios signados.

1.1)

• Sistemas de numeración posicionales:

En un sistema de esta clase, un número se representa por medio de una cadena de dígitos, donde cada posición del digito tiene un peso asociado. Así, el valor del número es una suma ponderada de los dígitos.

En un sistema posicional general, la base puede ser cualquier entero b
2, y un digito en la posición i tiene un peso bi; un punto base permite que se utilicen tanto potencias negativas como positivas de la base. La forma de expresión de un número N cualquiera es:

Donde existen n dígitos a la izquierda del punto base y p dígitos a la derecha. Si el punto se omite, se supone que se encuentra a la derecha del digito del extremo derecho.

El valor de dicho número puede representarse como una suma de potencias de la base, de la siguiente manera:

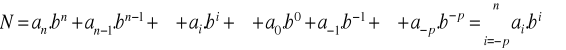
Siendo ai un número perteneciente al sistema y que, por lo tanto, cumple la condición 0
ai
b.

Excepto por la posibilidad de tener ceros al principio o al final, la representación de un número en un sistema de numeración posicional es única. El digito que esta en el extremo izquierdo se denomina “digito más significativo” y el digito que esta en el extremo derecho se denomina “digito menos significativo”.

• Sistema decimal:

Este es un sistema de base 10, donde se utilizan 10 símbolos (que forman la sucesión monótona creciente 0,1,2,3,4,5,6,7,8,9) para representar números. Cada peso es una potencia de 10 que corresponde a la posición del digito. Un punto decimal permite que se utilicen tanto potencias negativas como positivas de 10. La forma de expresión de un número D en esta base y su valor están dados por:

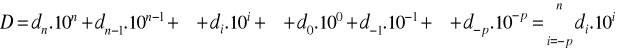
• Sistema binario:

Este es un sistema de base 2, donde solo se emplean 2 símbolos (0 y 1, llamados “bits”, por la contracción de las palabras “binary digits”). Cada peso es una potencia de 2 que corresponde a la posición del digito. Un punto binario permite que se utilicen tanto potencias negativas como positivas de 2. El sistema binario se emplea para representar señales en un sistema digital, ya que dichas señales se encuentran normalmente en uno de dos estados: alto (1) o bajo (0). La forma de expresión de un número B en esta base y su valor están dados por:

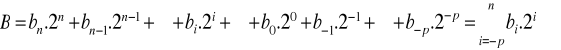
El bit que esta en el extremo izquierdo de un numero binario se conoce como el “bit más significativo” (MSB, most significant bit), y el bit que se encuentra en el extremo derecho se conoce como el “bit menos significativo” (LSB, least significant bit).

• Sistema octal:

Este es un sistema de base 8, que necesita 8 símbolos para representar números, de modo que se emplean los dígitos del 0 al 7 del sistema decimal. Este sistema es útil para representar números de múltiples bits, ya que su base es una potencia de 2. Puesto que una cadena de 3 bits puede tomarse en 8 diferentes combinaciones, se sigue que cada cadena de 3 bits puede representarse de manera única por un digito octal.

El sistema numérico octal no se utiliza mucho en la actualidad, a consecuencia de la preponderancia de las maquinas que procesan bytes compuestos de 8 bits.

• Sistema hexadecimal:

Este es un sistema de base 16, que necesita 16 símbolos para representar números, de modo que se emplean los dígitos del 0 al 9 del sistema decimal con las letras de la A hasta la F. Este sistema es útil para representar números de múltiples bits, ya que su base es una potencia de 2. Puesto que una cadena de 4 bits puede tomarse en 16 diferentes combinaciones, se sigue que cada cadena de 4 bits puede representarse de manera única por un digito hexadecimal.

En base al criterio anterior, en el sistema numérico hexadecimal, dos dígitos represen-tan un byte de 8 bits, y 2n dígitos representan una palabra de n bytes; en este contexto, un digito hexadecimal de 4 bits se denomina a veces un nibble (medio byte).

DECIMAL	BINARIO	OCTAL	CADENA DE 3 BITS	HEXADECIMAL	CADENA DE 4 BITS
0	0	0	000	0	0000
1	1	1	001	1	0001
2	10	2	010	2	0010
3	11	3	011	3	0011
4	100	4	100	4	0100
5	101	5	101	5	0101
6	110	6	110	6	0110
7	111	7	111	7	0111
8	1000	-	-	8	1000
9	1001	-	-	9	1001
10	1010	-	-	A	1010
11	1011	-	-	B	1011
12	1100	-	-	C	1100
13	1101	-	-	D	1101
14	1110	-	-	E	1110
15	1111	-	-	F	1111

• Conversión de un sistema a otro:

• Consideraciones preliminares:

En general, la conversión entre dos bases no puede hacerse por simple sustitución; se requieren operaciones aritméticas. Aquí enunciaremos una regla para convertir un número en cualquier base a un número en base 10, y viceversa.

- De base r a base 10:

Partimos del hecho conocido de que el valor de un número en cualquier base esta dado por la formula:

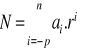
Donde r es la base del sistema en el cual se halla el número y existen n dígitos a la izquierda del punto base y p dígitos a la derecha. De esta forma, el valor del numero puede encontrarse al convertir cada digito del numero a su equivalente en base 10, y expandir la formula utilizando aritmética de base 10. Escribimos la formula de expansión de manera anidada:

Esto es, comenzamos con una suma de 0; iniciando con el digito que esta en el extremo izquierdo, multiplicamos la suma por r, y agregamos el siguiente digito a la suma, repitiendo este proceso hasta que todos los dígitos hayan sido procesados.

- De base 10 a base r:

Ahora, partimos de la formula anterior para fundamentar un método para convertir de un numero en base 10 a cualquier base. Para esto, consideremos ¿que ocurre si dividimos la formula entre r? Puesto que la parte entre paréntesis de la formula es igualmente divisible entre r, el cociente será:

Y el residuo será d0. De este modo, d0 puede calcularse como el residuo de la división larga de N entre r. Adicionalmente, el cociente Q tiene la misma forma que la formula original; por lo tanto, divisiones sucesivas entre r nos proporcionan dígitos sucesivos de N de derecha a izquierda, hasta que todos los dígitos de N hayan sido derivados.

• Conversión de Binario a…

- Octal:

Se hace a través de una sustitución directa. Desde el punto binario, se separa el número binario en grupos de 3 bits, que se reemplazan por su correspondiente digito octal.

Ejemplo:

- Hexadecimal:

Se hace a través de una sustitución directa. Desde el punto binario, se separa el número binario en grupos de 4 bits, que se reemplazan por su correspondiente digito hexadecimal.

Ejemplo:

- Decimal:

Se hace a través de la suma, convirtiendo cada digito del número a su equivalente en base 10 de acuerdo a la posición que ocupa, y luego sumándolos.

Ejemplo:

• Conversión de Octal a…

- Binario:

Se hace a través de una sustitución directa, reemplazándose cada digito octal por su equivalente grupo de 3 bits.

Ejemplo:

- Hexadecimal:

Se convierte primero el número octal a binario, reemplazándose cada digito octal por su correspondiente grupo de 3 bits. Luego, a partir del punto binario, se separa el número binario en grupos de 4 bits, que se reemplazan por su correspondiente digito hexadecimal.

Ejemplo:

- Decimal:

Se hace a través de la suma, convirtiendo cada digito del número a su equivalente en base 10 de acuerdo a la posición que ocupa, y luego sumándolos.

Ejemplo:

• Conversión de Hexadecimal a…

- Binario:

Se hace a través de una sustitución directa, reemplazándose cada digito hexadecimal por su equivalente grupo de 4 bits.

Ejemplo:

- Octal:

Se convierte primero el número hexadecimal a binario, reemplazándose cada digito hexadecimal por su correspondiente grupo de 4 bits. Luego, a partir del punto binario, se separa el número binario en grupos de 3 bits, que se reemplazan por su correspondiente digito octal.

Ejemplo:

- Decimal:

Se hace a través de la suma, convirtiendo cada digito del número a su equivalente en base 10 de acuerdo a la posición que ocupa, y luego sumándolos.

Ejemplo:

• Conversión de Decimal a…

- Binario:

Se hace a través de la división.

Ejemplo:

- Octal:

Se hace a través de la división.

Ejemplo:

- Hexadecimal:

Se hace a través de la división.

Ejemplo:

REGLA PRÁCTICA:

Dividir por el valor decimal de la base el número decimal a convertir, así como los sucesivos cocientes, hasta obtener un cociente menor al valor de la base.

Este último cociente y los restos de las divisiones efectuadas constituyen, en ese orden, el número buscado.

• Operaciones con números binarios:

• Suma de números binarios:

La siguiente es una tabla de sumar para números binarios:

0	+	0	=	0
0	+	1	=	1
1	+	0	=	1
1	+	1	=	0	y se acarrea un 1 a la siguiente columna

Para sumar dos números binarios X y Y, sumamos juntos los bits menos significativos, con un acarreo inicial de 0, produciendo bits de suma y bits de acarreo. Continuamos procesando bits de derecha a izquierda, sumando el acarreo (si lo hubiere) fuera de cada columna a la suma de la siguiente columna.

Ejemplo:

• Resta de números binarios:

La siguiente es una tabla de restar para números binarios:

0	-	0	=	0
0	-	1	=	1	y restamos un 1 de la siguiente columna
1	-	0	=	1
1	-	1	=	0

La resta binaria se realiza de manera similar a la suma, pero empleando acarreos negativos (“prestamos”) desde una columna a la columna anterior cuando el minuendo de esa columna sea un 0 y el sustraendo sea un 1. Para restar dos números binarios X y Y, restamos juntos los bits menos significativos con un préstamo inicial de 0, produciendo bits de resta y bits de préstamo. Continuamos procesando bits de derecha a izquierda, restando el bit de préstamo (si lo hubiere) a la siguiente columna.

Los valores del minuendo binario se modificaran cuando se presente el préstamo. Cada vez que se pide un 1 a la siguiente posición del minuendo, este pasara a ser 0. En el caso de que la siguiente también sea 0, pasara a ser 1, debiéndose pedir nuevamente un 1 a la subsiguiente posición, que también pasara a ser 1 si es 0, y así, sucesivamente, si hay 0 en el minuendo se transformaran en 1 hasta llegar a un 1 que pasara a ser 0.

Ejemplo:

• Multiplicación, división y potenciación de números binarios:

La siguiente es la tabla de multiplicar para números binarios:

0	x	0	=	0
0	x	1	=	0
1	x	0	=	0
1	x	1	=	1

Multiplicar en binario es muy sencillo: se repite el multiplicando desplazado a la izquierda, conforme a la posición que ocupen los unos del multiplicador. Luego se realiza la suma con los sumandos así ordenados.

Ejemplo:

La división se puede realizar con el método de las diferencias sucesivas, siendo que cada sustraendo se obtiene multiplicando por 1 al divisor si este ultimo es menor o igual que el resto parcial en cuestión, o por 0 si el mismo es mayor que dicho resto.

Ejemplo:

Es importante señalar que cada vez que se multiplica o se divide un número entero binario por la base 102=210, se agrega o se quita un cero, respectivamente.

Con respecto a la potenciación, en cualquier base, siempre que se tengan p factores iguales de un numero n, se podrá escribir nxnxnx…xn=np. Según sea la base, variará la representación de n y p.

Debe tenerse presente que en cualquier base, la unidad seguida de p ceros puede expresarse como la base a la potencia p, simbolizándose 10 la base en todos los sistemas numéricos.

Ejemplo:

1.2)

• Códigos:

Se entiende por código una representación univoca de las cantidades, de tal forma que a cada una de estas se asigna una combinación de símbolos determinados, y viceversa.

• Códigos binarios:

El sistema binario recibe el nombre de “código binario natural”. Con n cifras binarias o bits se pueden obtener 2n combinaciones diferentes. Cada combinación de estas se puede asignar a una cantidad diferente. Por ello, el número de asignaciones posible es el de permutaciones de las 2n combinaciones, es decir, 2n!, que constituyen otros tantos códigos binarios.

Un código binario es continuo si las combinaciones correspondientes a números decima-les consecutivos son adyacentes. Se denominan combinaciones binarias adyacentes aquellas que difieren solamente en un bit.

Un código binario es cíclico si la última combinación es adyacente a la primera.

• Código Gray:

Es un código binario cíclico no ponderado diseñado para reducir la probabilidad de que un sistema malinterprete una entrada cambiante, ya que solo 1 bit cambia entre cada par de palabras de código sucesivas.

Existen dos maneras convenientes de construir un código Gray con cualquier número deseado de bits. El primer método esta basado en el hecho de que el código Gray es un “código reflejado”; puede ser definido y construido de manera recursiva, empleando las siguientes reglas:

Un código Gray de 1 bit tiene dos palabras de código, 0 y 1.

Las primeras 2n-1 palabras de código de un código Gray de n bits son iguales a las palabras de código de un código Gray de n-1 bits, escritas en orden con un 0 agregado en su extremo izquierdo.

Las ultimas 2n-1 palabras de código de un código Gray de n bits son iguales a las palabras de código de un código Gray de n-1 bits, pero escritas en orden inverso y con un 1 agregado en su extremo izquierdo.

El segundo método nos permite derivar una palabra de código Gray de n bits directamente de la correspondiente palabra de un código binario natural de n bits.

Los bits de una palabra de código binaria de n bits o código Gray se enumeran de derecha a izquierda, desde 0 hasta n-1.

El bit i de una palabra de código de código Gray es 0 si los bits i e i+1 de la correspondiente palabra de código binario son iguales; sino, el bit i es 1 (cuando i+1=n, el bit n de la palabra de código binario se considera que es 0).

CÓDIGO BINARIO NATURAL	CÓDIGO GRAY
		1 BIT	2 BITS		3 BITS		4 BITS
0000	0	0	0	0	00	0	000
0001	1	0	1	0	01	0	001
0010	-	1	1	0	11	0	011
0011	-	1	0	0	10	0	010
0100	-	-	-	1	10	0	110
0101	-	-	-	1	11	0	111
0110	-	-	-	1	01	0	101
0111	-	-	-	1	00	0	100
1000	-	-	-	-	-	1	100
1001	-	-	-	-	-	1	101
1010	-	-	-	-	-	1	111
1011	-	-	-	-	-	1	110
1100	-	-	-	-	-	1	010
1101	-	-	-	-	-	1	011
1110	-	-	-	-	-	1	001
1111	-	-	-	-	-	1	000

• Códigos alfanuméricos:

Son códigos no ponderados que permiten representar, aparte de información numérica, información alfabética y algunos signos especiales (caracteres imprimibles), como así también caracteres de control del sistema, que pueden emplearse para controlar una acción, para señalar una condición, o para representar el estado actual del hardware (caracteres no imprimibles).

El código alfanumérico más utilizado es el código ASCII (American Standar Code for Information Interchange), que representa cada carácter con una cadena de 7 bits y produce un total de 27=128 caracteres diferentes, los cuales se indican en la siguiente tabla:

Descargar

b6b5b4

Enviado por:	Eduardo Daniel Andolfi
Idioma:	castellano
País:	Argentina