Matemáticas
Funciones especiales y propiedades de las funciones
COLEGIO DE BACHILLERES DEL ESTADO DE OAXACA
PLANTEL 39 NAZARENO ETLA
MATEMÁTICAS
FUNCIONES ESPECIALES Y PROPIEDADES DE LAS FUNCIONES
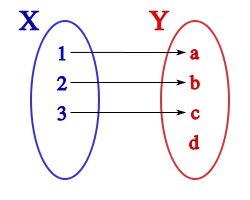
BAUTISTA LÓPEZ JENNIFER MARITZA
407
NAZARENO ETLA
1 Febrero 2009
FUNCIONES ESPECIALES
FUNCIÓN CONSTANTE
TRLAS QUE F(x)K CON K X ERSe llama función constante a la que no depende de ninguna variable, y la podemos representar como una función matemática de la forma:
![]()
Donde a es la constante.
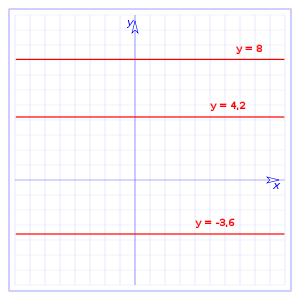
Como se puede ver es una recta horizontal en el plano xy, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:
![]()
Tenemos:
![]()
Donde a tiene un valor constante, en la gráfica tenemos representadas:
![]()
![]()
![]()
Como la variable dependiente y no depende de x tenemos que:
![]()
La variación de y respecto a x es cero
La función constante como un polinomio en x
Si un polinomio general, tiene la forma:
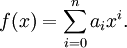
Una función constante cumple esta expresión con n= 0, es un polinomio de grado 0.

Que es lo mismo que:
![]()
Que corresponde al termino independiente del polinomio.
Grafica de la función constante
Es el conjunto de los puntos del plano que representan a los pares ordenados de la función, donde su primera componente es un número real y su segunda componente es el valor constante.
F= {(x,f(x)]
VALOR ABSOLUTO
en matemáticas, el valor absoluto o módulo[1] de un número real es su valor numérico sin su respectivo signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y -3.
El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los números reales, cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
El valor absoluto está estrechamente relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos.
Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.
2. Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.
3. Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.
4 Representamos la función resultante.
GRAFICA DE LA FUNCIÓN VALOR ABSOLUTO
Es el conjunto de puntos del plano que representa a los pares ordenados de la función en los cuales la primera componente es un numero real y la segunda componente ese el valor absoluto de la primera.
![]()
![]()

Propiedades de la función
a) INYECTIVA: Aquellas en que a cada imagen le corresponde un único origen. Formalmente,
![]()
o lo que es lo mismo,
![]()
a cada elemento del dominio corresponde el mismo numero como su imagen de manera que diferente elementos del dominio tienen la misma imagen.
C=3
Por lo tanto la función constante no es inyectiva. Todas las funciones constantes no son inyectivas
B) SUPRAYECTIVA: Aquellas en que la aplicación es sobre todo el codominio, es decir, cuando el conjunto imagen ![]()
. Esto significa que todo elemento del condominio tiene un origen. Formalmente,
![]()
Estas funciones también se conocen como exhaustivas o epiyectivas.
como el dominio y el contra dominio de la función son los números reales y cualquier le pertenece al conjunto de A le corresponde el mismo numero, entonces el conjunto imagen es igual a ej. C=3 y 3 =/ TR por consiguiente la función constante no es suprayectiva
c) BIYECTIVA: cuando la función es inyectiva y suprayect5iva ala vez, cumple la regla biyectiva por lo tanto depende de la fu8ncion
Aquellas que son al mismo tiempo inyectivas y sobreyectivas. Formalmente,
![]()
Ejemplos
Ejercicios
FUNCIÓN CONSTANTE
F(x)= 3x E1R F=[(x, F(x)]
VALORES F x =3 (X, F x)
-3 F (-3) =3 (-3,3)
-2 F (-2) =3 (-2,3)
-1 F (-1) =3 (-1,3)
0 F (0) =3 (0,3)
1 F (1) =3 (1,3)
2 F (2) =3 (2,3)
3 F (3) =3 (3,3)

Propiedades
Inyectiva:
Esta grafica no es inyectiva debido a que todos los elementos del dominio les corresponden el mismo contra dominio es decir para todos los elementos de a
C=3
Suprayectiva:
Tampoco es suprayectiva debido a que a todos los humeros de a les corresponde el mismo contra dominio
Biyectiva:
Al no ser inyectiva ni tampoco suprayectiva n cumple las reglas de esta y no es biyectiva
F(x)= -3
-3 F (-3) =-3 (-3,-3)
-2 F (-2) =-3 (-2,-3)
-1 F (-1) =-3 (-1,-3)
0 F (0) =-3 (0,-3)
1 F (1) =-3 (1,-3)
2 F (2) =-3 (2,-3)
3 F (3) =-3 (3,-3)
Propiedades
Inyectiva:
Esta grafrica no es inyectiva para que todos los elementos de X corresponden ala misma imagen es decir que en todos los casos
C=-3
Biyectiva:
No es biyectiva ya que estas a su vez no es ni inyectiva ni suprayectiva al mismo caso anterior y sus rangos corresponden a cualquier cantidad de los dominios.
Suprayectiva:
No es suprayectiva ya que aunque coincida en (-2,-2) el rango es el mismo para todos los dominios.
Ejercicios
VALOR ABSOLUTO
F(x)= -4
X F(x)=(x) (x, F(x))
-4 F (-4)=/-4/ (-4,4)
-3 F (-3)=/-3/ (-3,3)
-2 F (-2)=/-2/ (-2,2)
-1 F (-1)=/-1/ (-1,1)
0 F (0)=/0/ (0,0)
1 F (1)=/1/ (1,1)
2 F (2)=/2/ (2,2)
3 F (3)=/3/ (3,3)
4 F (4)=/4/ (4,4)
Propiedades
Inyectiva:
Esta grafica si es inyectiva ya que para los dominios siempre hay contra dominio diferente a los demás.
Suprayectiva:
Si es suprayectiva ya que a todos los elementos les corresponde más de un elemento y en este caso les corresponde dos as cada uno.
Biyectiva:
Si es biyectiva ya qu8e no se repite ningún para y los contra dominios cambian
Descargar
| Enviado por: | Jennifer Maritza Bautista Lopez |
| Idioma: | castellano |
| País: | México |