Matemáticas
Figuras cónicas
SECCIONES CÓNICAS
En geometría, una sección cónica es cualquier curva producida por la intersección de un plano y un cono recto triangular. Dependiendo del ángulo del plano relativo al cono, la intersección puede ser: un círculo, una elipse, una hipérbola o una parábola.
Apolonio de Perga (262-190 a. C.) fue el primero que escribió un tratado sobre estas curvas y les dio el nombre por el que se las conoce.
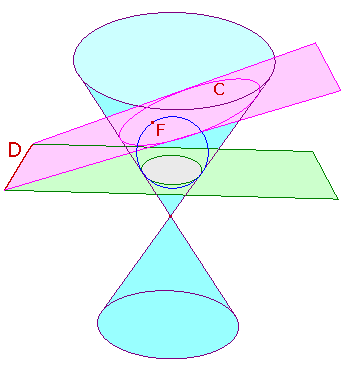
Las Cónicas se pueden describir como curvas planas que son los caminos de un punto en movimiento para que el radio de su distancia forme un punto arreglado (foco) a la distancia de la línea determinada (directriz) que es constante.
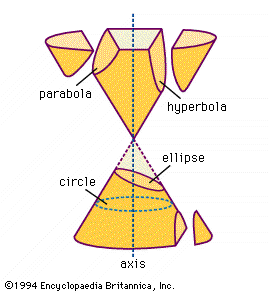
Si la excentricidad es cero, la curva forma un círculo, si es igual a dos, forma una parábola, si es menor a uno, forma una elipse, y si es mayor a uno, forma una hipérbola.
Elipse
La elipse es el conjunto de puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es una cantidad constante.
La sección es una elipse si inclinamos el plano de modo que sea oblicuo con el eje y corte a todas las generatrices.
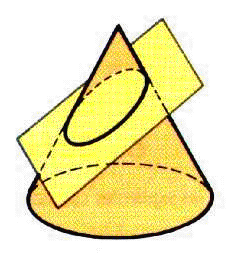
Entre más pequeña sea la distancia del foco, la excentricidad disminuirá y la elipse se parecerá más a un círculo. El eje menor es perpendicular al eje mayor por el centro en el punto en el que la distancia es igual que el foco.
El foco es simétrico a sus dos ejes, la curva formada cuando se rota la elipse se llama elipsoide de revolución, o esferoide.
La excentricidad es un número que mide el achatamiento mayor o menor de la elipse. Se define así:
e= c / a, c < a
La ecuación es:
x2 / a2 + y2 / b2 = 1, a, b > 0
Elementos de la elipse:
-
Los radios de vectores
-
El eje focal
-
El eje secundario
-
El centro de la elipse
-
La distancia focal
-
Los vértices
-
El eje mayor y el eje menor
Hipérbola
La hipérbola es el conjunto de puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es una cantidad constante. La hipérbola por su simetría, tiene dos focos.
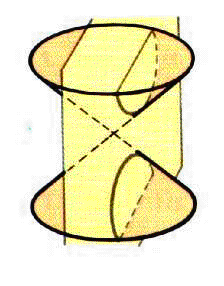
Si una línea es dibujada por el foco y prolongada después del eje transversal de la hipérbola, perpendicular a ese eje, e intersectándolo en el centro geométrico de la hipérbola, un punto a la mitad entre los dos focos, ahí se encuentra el eje conjugado. La hipérbola es simétrica con respecto a sus dos ejes.
Dos líneas simétricas, las asíntotas de la curva, pasan por el centro geométrico. La hipérbola no toca las asíntotas, pero su distancia con ellas se acorta, pero nunca llegan a interceptarse.
La excentricidad es un número que mide la abertura mayor o menor de las ramas de la hipérbola. Se define así:
e= c / a, c > a
La ecuación es:
x2 / a2 - y2 / b2 = 1, a, b > 0
Elementos de la hipérbola:
-
Los radios de vectores
-
El eje focal
-
El centro de la hipérbola
-
La distancia focal
-
Los vértices
-
El eje transversal o eje real
-
El eje no transverso o eje imaginario
Parábola
Una parábola es una curva abierta, producida por la intersección de un cono circular recto y un plano paralelo a algún elemento del cono.
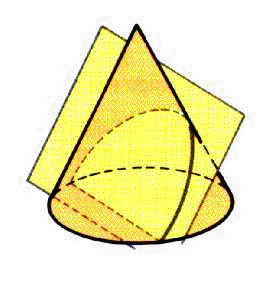
La parábola es el conjunto de puntos que está a la misma distancia de un punto, su foco, y una recta fija, su directriz.
El vértice y el foco determinan una línea perpendicular a la directriz, a ésta línea se le conoce como el eje de la parábola.
Cuando el vértice es (0, 0) la ecuación es:
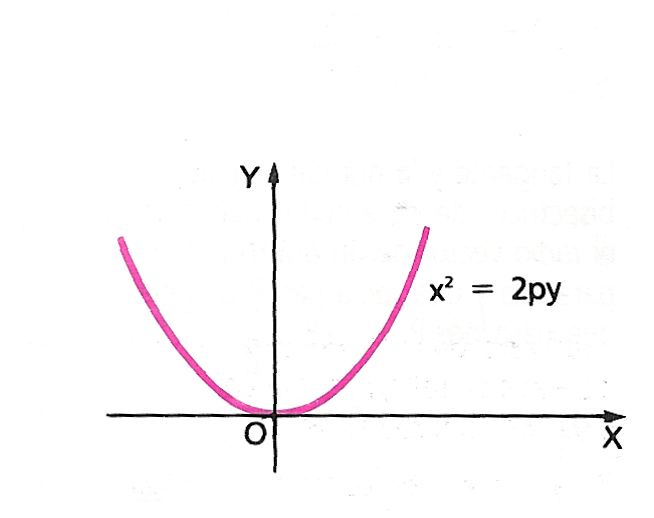
x2 = 2 p y
Cuando el eje es paralelo al eje 0Y y el vértice está en el punto V (X0 , Y0), la ecuación es de la forma:
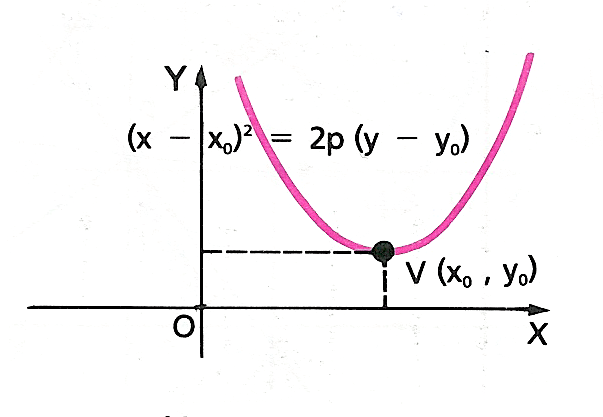
(x - x0)2 = 2p (y - y0)
Elementos de la parábola:
-
El foco
-
La directriz
-
El radio vector
-
El parámetro
-
El eje de la parábola
-
El vértice
Circunferencia
Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. El radio de la circunferencia es la distancia de un punto cualquiera de dicha circunferencia, al centro.

Puede ser definida como una curva plana que es el camino de un punto al moverse, para que el radio de la distancia desde algún punto fijo (foco), hacia la distancia de otro punto fijo (directriz), sea igual a cero.

Ecuación de la circunferencia de centro (a, b) y radio r; si P (x, y) es un punto cualquiera de la circunferencia, se verifica:
(x - a)2 + (y - b)2 = r2
La igualdad anterior representa la ecuación de una circunferencia de centro C (a, b) y radio r.
Efectuando las operaciones indicadas, se obtiene:
x2 + a2 - 2ax + y2 + b2 - 2by = r2
x2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0
Si hacemos D = - 2a, E = - 2b y F = a2 + b2 - r2, la ecuación se expresa en la forma:
x2 + y2 + Dx + Ey + F = 0
.
1
Descargar
| Enviado por: | Sara |
| Idioma: | castellano |
| País: | España |
