Matemáticas
Fibonacci
INTRODUCCIÓN
Desde los tiempos más antiguos los números han cautivado al ser humano, no solo por su aplicación inmediata a la vida cotidiana sino por la riqueza teórica y simple que se encuentra dentro de ellos. Existe una gran cantidad de números con propiedades especiales, entre ellos se pueden citar los números primos, números perfectos, números amigos, sociables, etc. Como puede verse la lista es bastante larga y lo más interesante es que cada clase de éstas ha conducido a importantes e interesantes estudios teóricos. Los números de Fibonacci son algunos de los que más frutos han dado, pues cuentan con asiduos matemáticos y aficionados que se han dedicado a la búsqueda de las relaciones mas insospechadas de estos números y que han encontrado resultados de estas características en la mano humana, en los pétalos de una flor, las espirales de los girasoles, las espirales de las piñas, la altura de la cadera, la altura de la rodilla, la altura de un ser humano y la altura de su ombligo, la cría de los conejos, la Mona Lisa, y otras más que desarrollaré a continuación.
Biografía de Fibonacci
Leonardo de Pisa, mejor conocido por su apodo Fibonacci (que significa hijo de Bonacci) nació en la ciudad italiana de Pisa y vivió de 1170 a 1250. Su padre trabajaba como representante de la casa comercial italiana más importante de la época, en el norte de África. Este lo animó a estudiar matemáticas. Leonardo recibió este tipo de enseñanza de maestros árabes. Se convirtió en un especialista en Aritmética y en los distintos sistemas de numeración que se usaban entonces. Convencido de que el sistema indo-arábigo era superior a cualquiera de los que estaban en uso, decidió llevar este sistema a Italia y a toda Europa, en donde aún se usaban los numerales romanos y el ábaco. Escribió gran cantidad de libros y textos de matemáticas: Liber Abaci escrito en 1202, Practica Geometriae en 1220, Flos en 1225 y Liber Quadratorum en 1227. Es importante destacar que en esa época no existía la imprenta, por lo tanto los libros y sus copias eran escritos a mano. Fue sin duda el matemático más original de la época medieval cristiana.
Sucesión de Fibonacci
Una sucesión de Fibonacci es aquella cuya ley de recurrencia es:
an = an-1 + an-2
Es decir, cada término de la sucesión se obtiene sumando los dos anteriores. Para empezar a construirla necesitamos, por tanto, dos números de partida, a1 y a2. De esta forma, a3 sería a2 + a1 ; a4 sería a3 + a2 y así sucesivamente.
La más conocida es la que tiene a1 = 1 y a2 = 1, cuyos términos son:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 ...
Números que son conocidos como Números de Fibonacci.
Los términos de cualquier sucesión de Fibonacci tienen la particularidad de que el cociente entre dos términos consecutivos se aproxima al Número de Oro (1.6180339887499...), es decir, el límite de los cocientes an+1/an tiende al Número de Oro cuando n tiende a infinito.
Además, las series de Fibonacci cumplen otras curiosas propiedades, como por ejemplo, que la suma de n términos es igual al término n+2 menos uno:
a1 + a2 + a3 + a4 +..... + an-1 + an = an+2 - 1
El número de oro
El número áureo o de oro (también llamado número dorado, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en honor a Leonardo de Pisa Fibonacci), es el número irracional:
![]()
Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza en elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, etc.
Asimismo, se atribuye un carácter estético especial a los objetos que siguen la razón áurea, así como una importancia mística. A lo largo de la historia, se le ha atribuido importancia en diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido objetables para las matemáticas y la arqueología.
Se dice que dos números positivos a y b están en razón áurea si y sólo si:
![]()
Para obtener el valor de ![]()
a partir de esta razón considere lo siguiente:
Que la longitud del segmento más corto b sea 1 y que la de a sea x. Para que estos segmentos cumplan con la razón áurea deben cumplir que:
![]()
Multiplicando ambos lados por x y reordenando:
![]()
Mediante la fórmula general de las ecuaciones de segundo grado se obtiene que las dos soluciones de la ecuación sean:
![]()
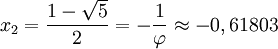
La solución positiva es el valor del número áureo.
Los pitagóricos obtuvieron este número de hallar la relación entre la diagonal del pentágono regular y su lado. Esta proporción se puede encontrar en muchas obras de arte.
En la Torre Eiffel de París la razón entre la altura de un nivel y el precedente guarda la relación áurea.
En el cuadro “Atomic Leda” Salvador Dali hizo uso también de la proporción áurea.


En la Mona Lisa la cara está perfectamente encuadrada en un rectángulo áureo, al igual que el resto de proporciones de la misma.
La serie de fibonacci
0, 1, 1, 2, 3, 5, 8, 13, 21, 34...
Es aquella en la que cada número, a partir del tercero, se obtiene sumando los dos que le preceden. Los cocientes entre dos números consecutivos se aproximan cada vez más al número de oro según se avanza en la sucesión.
2/1 = 2, 3/2 = 1,5, 5/3 = 1,66, 8/5 = 1,6, 13/8 = 1,625, 21/13 = 1,615...
La espiral logarítmica basada en la relación áurea
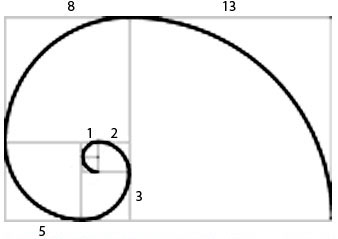
Partimos de un cuadrado de lado 1 y añadimos otro cuadrado de lado también igual a 1, para formar un rectángulo de 2x1. Añadimos otro cuadrado de 2x2 para formar otro rectángulo de 3x2 (siguiendo la serie de fibonacci) y después un cuadrado de 3x3 teniendo un rectángulo de 5x3 y así sucesivamente. Trazando un cuarto de círculo con origen del mismo desde un vértice de cada cuadrado obtendremos la espiral.
Las pirámides de Egipto, construidas cuatro mil años antes de que Fibonacci diera con la serie, fueron construidas manteniendo una sorprendente proporción áurea.

El Partenón griego fue construido también respetando las proporciones áureas.

Naturaleza
- Existen cristales de Pirita dodecaedritos pentagonales (piritoedros) cuyas caras son pentágonos perfectos.
- Leonardo de Pisa (Fibonacci), en su Libro de los ábacos (Liber abacci, 1202, 1228), usa la sucesión que lleva su nombre para calcular el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos están aislados por muros, se empiezan a reproducir cuando tienen dos meses de edad, tardan un mes desde la fecundación hasta la parición y cada camada es de dos conejos). Este es un problema matemático puramente independiente de que sean conejos los involucrados. En realidad, el conejo común europeo tiene camadas de 4 a 12 individuos y varias veces al año, aunque no cada mes, pese a que la preñez dura 32 días. El problema se halla en las páginas 123 y 124 del manuscrito de 1228, que fue el que llegó hasta nosotros, y parece que el planteo recurrió a conejos como pudiera haber sido a otros seres; es un soporte para hacer comprensible una incógnita, un acertijo matemático. El cociente de dos términos sucesivos de la Sucesión de Fibonacci tiende a la sección áurea o al número áureo si la fracción resultante es propia o impropia, respectivamente. Lo mismo sucede con toda sucesión recurrente de orden dos, según demostraron Barr y Schooling en la revista The Field del 14 de diciembre de 1912.[3]
- La relación entre la cantidad de abejas macho y abejas hembra en un panal.
- La disposición de los pétalos de las flores (el papel del número áureo en la botánica recibe el nombre de Ley de Ludwig).
- La distribución de las hojas en un tallo. Ver: Sucesión de Fibonacci.
- La relación entre las nervaduras de las hojas de los árboles
- La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a Φ tomando como unidad la rama superior).
- La distancia entre las espirales de una Piña.
- La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol o de cefalópodos como el nautilus hay por lo menos tres espirales logarítmicas más o menos asimilables a proporciones aúreas. La primera de ellas se caracteriza por la relación constante igual al número áureo entre los radiovectores de puntos situados en dos evolutas consecutivas en una misma dirección y sentido. Las conchas del Fusus antiquus, del Murex, de Scalaria pretiosa, de Facelaria y de Solarium trochleare, entre otras, siguen este tipo de espiral de crecimiento.[4] [5] Se debe entender que en toda consideración natural, aunque involucre a las ciencias consideradas más matemáticamente desarrolladas, como la Física, ninguna relación o constante que tenga un número infinito de decimales puede llegar hasta el límite matemático, porque en esa escala no existiría ningún objeto físico. La partícula elemental más diminuta que se pueda imaginar es infinitamente más grande que un punto en una recta. Las leyes observadas y descriptas matemáticamente en los organismos las cumplen transgrediéndolas orgánicamente.[6]
- Para que las hojas esparcidas de una planta (Ver Filotaxis) o las ramas alrededor del tronco tengan el máximo de insolación con la mínima interferencia entre ellas, éstas deben crecer separadas en hélice ascendente según un ángulo constante y teóricamente igual a 360º (2 - φ) ≈ 137º 30' 27,950 580 136 276 726 855 462 662 132 999..." En la naturaleza se medirá un ángulo práctico de 137º 30' o de 137º 30' 28" en el mejor de los casos. Para el cálculo se considera iluminación vertical y el criterio matemático es que las proyecciones horizontales de unas sobre otras no se recubran exactamente. Aunque la iluminación del Sol no es, en general, vertical y varía con la latitud y las estaciones, esto garantiza el máximo aprovechamiento de la luz solar. Este hecho fue descubierto empíricamente por Church y confirmado matemáticamente por Weisner en 1875. En la práctica no puede medirse con tanta precisión el ángulo y las plantas lo reproducen "orgánicamente"; o sea, con una pequeña desviación respecto al valor teórico. En la cantidad de elementos constituyentes de las espirales o dobles espirales de las inflorescencias, como en el caso del girasol, y en otros objetos orgánicos como las piñas de los pinos se encuentran números pertenecientes a la sucesión de Fibonacci.
Música
En toda canción, la melodía se basa en un conjunto de notas que llevan asociado un patrón. Existen múltiples maneras de combinarlas, para suerte de todos, pero ciertas sucesiones son tan buenas que pueden repetirse en muchas composiciones, resultando en fórmulas distintas pero que realmente tiene la misma base. Por decirlo de otra forma es como en las sucesiones de números; existen muchas pero alguna son tan interesantes y prácticas que pueden encontrarse en múltiple sitios, como la secuencia de Fibonacci.
Existen diferentes autores, como es el caso de Béla Bartók (1881-1945), que han utilizado dicha sucesión como patrón para determinar ciertos elementos de sus composiciones. Dicho autor desarrolló una escala musical basándose en la sucesión que denominó escala fibonacci. Así mismo, en su obra Música para instrumentos de cuerda, percusión y celesta, un análisis de su fuga muestra la aparición de la serie y de la razón áurea. Por otra parte, estudios realizados acerca de la Quinta sinfonía de Beethoven (1770-1827) muestran como el tema principal incluido a lo largo de la obra, está separado por un número de compases que pertenece a la sucesión. También en varias sonatas para piano de Mozart (1756-1791) la proporción entre el desarrollo del tema y su introducción es la más cercana posible a la razón áurea.
Relaciones matemáticas de este estilo se han encontrado también en la coral situada al final de Kunst der Fuge de Johann Sebastián Bach (1685-1750). En ella determinados motivos se repiten, por disminución a escalas menores, una y otra vez con distintas variaciones dentro de una región mayor de la pieza. Así, por ejemplo, varias voces repiten al doble de velocidad la melodía de la voz principal. Este es un ejemplo de pieza musical auto semejante, que, como veremos más adelante, es una característica de la geometría fractal, un concepto matemático de finales del siglo XX. Existen trabajos que analizan la manifestación de estas características fractales en otras obras, como en el tercer movimiento de la sonata numero 15 de Beethoven y el triángulo de Sierpinski, o la analogía entre el conjunto de Cantor y la primera Ecossaisen de Beethoven.
Arquitectura

Leonardo da Vinci realiza una visión del hombre como centro del Universo al quedar inscrito en un círculo y un cuadrado. El cuadrado es la base de lo clásico: el módulo del cuadrado se emplea en toda la arquitectura clásica, el uso del ángulo de 90º y la simetría son bases grecolatinas de la arquitectura. En él se realiza un estudio anatómico buscando la proporcionalidad del cuerpo humano, el canon clásico o ideal de belleza.
El hombre de Vitrubio es un claro ejemplo del enfoque globalizador de Leonardo Da Vinci que se desarrolló muy rápidamente durante la segunda mitad de la década de 1480. Trataba de vincular la arquitectura y el cuerpo humano, un aspecto de su interpretación de la naturaleza y del lugar de la humanidad en el "plan global de las cosas". En este dibujo representa las proporciones que podían establecerse en el cuerpo humano (por ejemplo, la proporción áurea). Para Leonardo, el hombre era el modelo del universo y lo más importante era vincular lo que descubría en el interior del cuerpo humano con lo que observaba en la naturaleza.
La Proporciones del Hombre de Vitruvio
Vitrubio el arquitecto, dice en su obra sobre arquitectura que la naturaleza distribuye las medidas del cuerpo humano como sigue: que 4 dedos hacen 1 palma, y 4 palmas hacen 1 pie, 6 palmas hacen 1 codo, 4 codos hacen la altura del hombre. Y 4 codos hacen 1 paso, y que 24 palmas hacen un hombre; y estas medidas son Ls que él usaba en sus edilicios. Si separas la piernas lo suficiente como para que tu altura disminuya 1/14 y estiras y subes los hombros hasta que los dedos corazón estén al nivel del borde superior de tu cabeza, has de saber que el centro geométrico de tus extremidades separadas estará situado en tu ombligo y que el espacio entre las piernas será un triángulo equilátero. La longitud de los brazos extendidos de un hombre es igual a su altura. Desde el nacimiento del pelo hasta la punta de la barbilla es la décima parte de la altura de un hombre; desde la punta de la barbilla a la parte superior de la cabeza es un octavo de su estatura; desde la parte superior del pecho al extremo de su cabeza será un sexto de un hombre. Desde la parte superior del pecho al nacimiento del pelo será la séptima parte del hombre completo. Desde los pezones a la parte de arriba de la cabeza será la cuarta parte del hombre. La anchura mayor de los hombros contiene en sí misma la cuarta parte de un hombre. Desde el codo a la punta de la mano será la quinta parte del hombre; y desde el codo al ángulo de la axila será la octava parte del hombre. La mano completa será la décima parte del hombre; el comienzo de los genitales marca la mitad del hombre. El pie es la séptima parte del hombre. Desde la planta del pie hasta debajo de la rodilla será la cuarta parte del hombre. Desde debajo de la rodilla al comienzo de los genitales será la cuarta parte del hombre. La distancia desde la parte inferior de la barbilla a la nariz y desde el nacimiento del pelo a las cejas es, en cada caso, la misma, y, como la oreja, una tercera parte del rostro.
Después de Leonardo, artistas como Ralaei y Miguel ángel hicieron un eran uso de la Sección Áurea para construir sus obras. La impresionante escultura de Miguel Ángel El David se ajusta en varios sentidos a la Sección Áurea, desde la situación del ombligo con respecto a la altura, hasta la colocación de las articulaciones de los dedos.
Los constructores de las iglesias medievales y góticas y de las catedrales europeas también erigieron estas asombrosas estructuras para adaptarse a la Sección Aurea. En este sentido, Dios realmente estaba en los números.
El número áureo en el misticismo
En la cruz latina, símbolo del catolicismo, la relación entre el palo vertical y el horizontal es el número áureo. Así mismo, el palo horizontal divide al vertical en secciones áureas.
La sucesión de Fibonacci en la cultura popular
- En la pág. 61 de la novela de Dan Brown El código Da Vinci aparece una versión desordenada de los primeros ocho números de Fibonacci (13, 3, 2, 21, 1, 1, 8, 5), que funcionan como una pista dejada por el conservador del museo del Louvre, Jacques Saunière.
- En el álbum Lateralus de la banda estadounidense Tool, los patrones de la batería (Danny Carey) de la canción "Lateralus" siguen la Sucesión de Fibonacci del número 13 (número de pistas del disco): 1,1,2,3,5,8,13,1,1,2,3,5,8,13,1,1,...
- En la miniserie Abducidos, la Sucesión de Fibonacci, como la Ecuación de Dios, es descubierta en los planes de los extraterrestres, en ejemplos como que sus naves tienen 5 tripulantes, sus manos 3 dedos y un pulgar, 1597 avistamientos ovnis en año anterior, se siguieron a 55 parejas para descubrir la hibrida humano-extraterrestre Allie, y que finalmente el número de abducidos era de 46368. Incidentalmente se habla en de un hombre que fue abducido 13 veces. 1, 3, 5, 13, 55, 1597, 46368, todos números Fibonacci.
- En el filme de Darren Aronofsky π el orden del caos el judío Rabbi Cohen presenta la teoría en hebreo transcrito en números en la cual el personaje Max Cohen relaciona esta última teoría con la secuencia de Fibonacci llegando en conclusión que todo esta basado en la ley del orden y el caos.
- En un lateral de la cúpula de la antigua sinagoga ahora convertida en el Museo Nazionale del Cinema, más conocida como Mole Antonelliana, en Torino (Italia), se puede observar una instalación luminosa de la sucesión de números de Fibonacci.
- El Dr. Walter Bishop de la serie de televisón Fringe usa numeros de la serie de Fibonacci para las contraseñas de sus cajas de seguridad.
CONCLUSIÓN
El número de oro es un número importante en todo lo que nos rodea, ya que se llegó a descubrir la multitud de situaciones de la vida cotidiana en las que aparece; es utilizado tanto en la naturaleza, como en el arte y en las matemáticas. La sucesión de Fibonacci es una proporción muy precisa, y gracias a esto se han representado grandes cuadros como es “El hombre de Vitrubio” de Leonardo Da Vinci.
BIBLIOGRAFÍA
http://www.centraldeclases.com/index.php?option=com_content&task=view&id=61&Itemid=66
http://fhi-design.com/musica1.htm
http://www.culturageneral.net/pintura/cuadros/jpg/hombre_de_vitruvio.jpg
http://es.shvoong.com/exact-sciences/engineering/architecture/260240-el-hombre-vitruvio/
http://www.geocities.com/athens/acropolis/4329/fibonac.htm
http://es.wikipedia.org/wiki/Sucesi%C3%B3n_de_Fibonacci
http://www22.brinkster.com/nosolomates/ayuda/fibonacci.htm
http://es.wikipedia.org/wiki/N%C3%BAmero_%C3%A1ureo
http://www.portalplanetasedna.com.ar/divina_proporcion.htm
http://www.juanramonruiz.com/2008/03/fibonacci-el-secreto-de-la-mona-lisa.html
11
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | Argentina |
