Física
Experimentos de física
MEDIDAS DE LONGITUDES Y MASAS
Introducción y Objetivo:
La mayor parte de los experimentos requieren la determinación de propiedades, de los objetos sometidos a estudio, tales como la longitud y la masa. Para realizar estas medidas se necesita echar mano de instrumentos, en algunos casos muy comunes (pesas, reglas) y en otros, más precisos (calibres, micrómetros, balanzas de precisión,...).
En esta primera práctica se utilizarán diversos instrumentos de medida con el fin de familiarizarse con ellos, aprender a manejarlos y a elegir el más apropiado según el caso.
Material:
-
Regla graduada (1)
-
Balanza de laboratorio (2)
-
Calibre (3)
-
Micrómetro (4)
-
Diversos objetos de materiales y formas diferentes

(1)
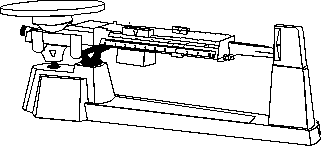
(2)
(3)

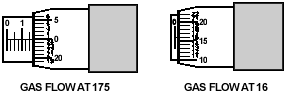

(4)
Parte experimental:
Antes de comenzar las medidas habrá que caracterizar los instrumentos de que se van a utilizar. Esta caracterización la mostramos en la Tabla 1.
Tabla 1: Caracterización de los instrumentos de medida
| Instrumento | Unidad más pequeña que puede apreciar (mm) | Error de cero (mm) |
| Flexómetro | 1.0 | 0 |
| Calibre | 5.0·10 ² | 0 |
| Micrómetro | 1.0·10 ² | - 5.0·10 ³ |
| Balanza | 1.0·10 ¹ | 0 |
Determinación del grosor de una hoja de papel:
Para realizar este experimento se miden en primer lugar el grosor de 100 hojas y luego se calcula el promedio por hoja. Primero se medirán con la regla (o flexómetro) y luego con el calibre. Como complemento se mide el grosor de una sola hoja mediante el micrómetro. (Los datos resultantes se muestran en la Tabla 2).
Tabla 2: Medidas de espesores
|
| Regla | Regla | Calibre | Calibre | Micrómetro |
| Lectura | Espesor de 100 hojas (mm) | Espesor promedio de 1 hoja (mm) | Espesor de 100 hojas (mm) | Espesor promedio de 1 hoja (mm) | Espesor de 1 hoja (-5.0·10-3 ) (mm) |
| 1 | 10 | 1.0·10 ¹ | 8.7 | 8.7·10 ² | 9.0·10 ² |
| 2 | 9.0 | 9.0·10 ² | 9.0 | 9.0·10 ² | 9.0·10 ² |
| 3 | 9.0 | 9.0·10 ² | 9.0 | 9.0·10 ² | 9.0·10 ² |
| Promedio | 9.0·10 ² | 8.9·10 ² | 9.0·10 ² |
- Grosor promedio de una hoja medido con regla = 9.0·10 ² mm
- Grosor promedio de una hoja medido con calibre = 8.9·10 ² mm
- Grosor de una hoja medido directamente con el micrómetro = 9.0·10 ² mm
Determinación experimental de π:
Se trata de calcular experimentalmente el valor de la constante π. Se coge un objeto cilíndrico y se mide su diámetro mediante el micrómetro. A continuación, se mide la longitud de su circunferencia con el calibre (el método será: marcando un punto en el objeto y haciéndolo rodar sobre un papel). Las medidas se repiten tres veces. Por último, se utiliza la expresión de la longitud de la circunferencia para calcular π. (Los resultados se muestran en la Tabla 3).
Tabla 3: Dimensiones de un objeto circular
| Medida | Diámetro (- 5.0·10-3) Micrómetro (mm) | Circunferencia Calibre (mm) |
| 1 | 22.23 | 71.00 |
| 2 | 22.23 | 70.00 |
| 3 | 22.23 | 71.00 |
| Promedio | 22.23 | 70.67 |
Ahora calculamos el valor de π resultante:
L = π · d ; 70.67 = π · 22.23 ; π = 3.18
Como se puede observar, el valor obtenido es distinto al valor aceptado (π = 3.14159).
Así, se calcula el % de error cometido en el experimento.
| valor medido - valor aceptado |
% error = --------------------------------------- x 100
valor aceptado
| 3.18 - 3.14 |
% error = -------------------- x 100 = 1.3%
3.14
Determinación de densidades:
Se determinan las densidades de diversos objetos de diferente forma.
m
A partir de la expresión de la densidad, ρ = ------- , se calcula la masa de cada objeto y
V
sus medidas de longitud (a continuación ya se puede calcular su volumen y por consiguiente su densidad).
Primero se realizan las medidas de longitud (se recogen en la Tabla 4).
Tabla 4: Medidas de longitud en el experimento de determinación de densidades
| Tubo | Hilo | Esfera | Lámina Rectangular
| Instru-mento | Calibre | Calibre | Calibre | Micró- metro | Cali-bre | Calibre | Calibre | Micró-metro | Cali-bre |
|
| ∅ Ext. | ∅ Int. | Largo | ∅ | Lar- go | ∅ | Largo | Ancho | Alto |
| 1 | 9.50 | 7.30 | 43.0 | 1.34 | 69.2 | 9.20 | 54.6 | 2.40 | 46.0 |
| 2 | 9.50 | 7.30 | 42.9 | 1.33 | 69.4 | 9.20 | 54.6 | 2.40 | 45.5 |
| 3 | 9.50 | 7.30 | 43.0 | 1.34 | 69.2 | 9.20 | 55.0 | 2.40 | 46.0 |
| Media | 9.50 | 7.30 | 43.0 | 1.34 | 69.3 | 9.20 | 54.7 | 2.40 | 45.8 |
Lectura de cero:
Calibre = 0 mm ; Micrómetro = -5.0·10-3 mm
Tomadas todas estas medidas, se realizan los cálculos necesarios para hallar los volúmenes de los objetos.
Tubo:
Vtubo = π· h · (R²-r²)
Vtubo = π · 43.0 · [(4.75) ²-(3.65) ²] ; Vtubo = π · 43.0 · (9.24)
Vtubo = 1250 mm³ ⇒ Vtubo = 1.25 cm³
Hilo:
Vhilo = π · r² · h
Vhilo = π · (1.34) ² · 69.3 ; Vhilo = π · 1.80 · 69.3
Vhilo = 392 mm³ ⇒ Vhilo = 3.92·10-1cm³
Esfera:
Vesfera = 4/3 · π · r³
Vesfera = 4/3 · π · (4.6) ³ ; Vesfera = 4/3 · π · 97.34
Vesfera = 408 mm³ ⇒ Vesfera = 4.08·10 ¹ cm³
Lámina Rectangular:
Vlámina = Largo · Alto · Ancho
Vlámina = 54.7 · 45.8 · 2.40
Vlámina = 6010 mm³ ⇒ Vlámina = 6.01 cm³
Ahora se realizan las medidas de masas para completar el experimento:
Tabla 5: Comparación de los valores de densidades calculados experimentalmente
| Objeto | Masa (gramos) | Volumen (cm³) | Densidad (EXP) (g/ cm³) | Densidad (ACP) (g/ cm³) | Error (%) |
| Tubo Tipo de material: Latón | 9.90 | 1.25 | 7.92 | 8.47 | 6.50 |
| Hilo Tipo de material: Cobre | 2.50 | 3.92·10-1 | 6.38 | 8.96 | 28.8 |
| Esfera Tipo de material: Acero | 3.60 | 4.08·10 ¹ | 8.82 | 7.86 | 12.2 |
| Lámina Rectang. Tipo de material: Acero | 38.4 | 6.01 | 6.40 | 7.86 | 18.5 |
Cálculo de densidades experimentales y sus errores:
ρ = m/V
9.90 | 7.92 - 8.47 |
ρ Tubo = ------------- = 7.92 g/cm³ ; % error = ---------------------- x 100 = 6.50 %
1.25 8.47
2.50 | 6.38 - 8.96|
ρ Hilo = ----------------- = 6.38 g/cm3 ; % error = ---------------------- x 100 = 28.8 %
3.92·10-1 8.96
3.60 | 8.82 - 7.86 |
ρ Esfera = ------------------ = 8.82 g/cm³ ; % error = -------------------- x 100 = 12.2 %
4.08·10 ¹ 7.86
38.4 | 6.40 - 7.86 |
ρ Lámina = ----------- = 6.40 g/cm³ ; % error = -------------------- x 100 = 18.5 %
6.01 7.86
Cuestiones relativas a la práctica:
¿Qué tipo de incertidumbre introduce en las medidas de longitud el error de cero?
El error de cero se debe a una deficiencia del aparato de medida y por lo tanto, la incertidumbre introducida es una incertidumbre sistemática.
La escala principal de un calibre está dividida en medios milímetros y su nonius tiene 20 divisiones. ¿Cuál es la precisión de este aparato?
La precisión del aparato será 0.025 mm.
Con el calibre de la anterior cuestión se mide una distancia de 12.5...mm, y la división número 13 del nonius coincide con una división de la regla. ¿Cuál es el resultado de la medida?.
Para saber las siguientes cifras significativas, habrá que multiplicar la división coincidente por la precisión del aparato. Así: 13 x 0.025 = 0.325mm. Entonces, la medida será 12.5325 mm.
Cuando se midió el espesor de una hoja de papel. ¿Cuál crees que fue el mejor método? ¿En qué caso se obtiene un resultado con mayor número de cifras significativas? ¿Coinciden los valores promedio calculados con los tres instrumentos? ¿A qué se deben las discrepancias si es que las hay?
Vistos los resultados, el mejor método parece la medición de una sola hoja con el micrómetro, ya que es el aparato que da mayor precisión (teniendo en cuenta el espesor de la hoja medido en todos los casos).
El resultado con mayor número de cifras significativas se obtiene en las medidas tomadas con el micrómetro y el calibre.
Los tres valores promedios calculados coinciden (una pequeña variación en una de las tres medidas hechas con el calibre pero teniendo en cuenta las dos últimas y las de los otros aparatos se podría despreciar esta primera).
Al determinar el grosor de la hoja de papel, si se hubiese utilizado sólo una décima parte de las hojas, ¿Cuántas cifras significativas tendría el resultado?¿Cómo se ve afectado el resultado por el número de hojas que se miden?
El resultado tendría el mismo número de cifras significativas que si se utilizasen 100 hojas. Por lo tanto, el número de hojas, en este caso, no afectaría al resultado.
La corrección de cero del micrómetro ¿tendrá mayor efecto sobre la medida del grosor de una hoja de papel o sobre el diámetro de las piezas cilíndricas utilizadas en este experimento?. Explíquese.
Esta corrección de cero tendrá mayor efecto en la medición del grosor de una hoja de papel que en la medición del diámetro de un cilindro.
El grosor de una hoja nos dará un resultado muy pequeño; por otra parte, el error sistemático también se tratará de una cantidad muy pequeña. Así, la corrección de cero influirá en la medida (debiendo corregirla). Por otra parte, el diámetro de cualquiera de las piezas cilíndricas utilizadas será sensiblemente mayor que el error sistemático, por lo que no influirá en la medida (pudiendo en algunos casos, según las cifras significativas adecuadas, despreciarse).
¿Depende el número de cifras significativas en el valor calculado del volumen del cilindro de si se utiliza un calibre o un micrómetro? Explíquese.
No depende ya que la medida del calibre y del micrómetro se da con el mismo número de cifras significativas (hasta las centésimas) y las cifras para los demás valores, cuando se determina el volumen, son los mismos en ambos casos.
En las medidas del cilindro, ¿qué está determinada con mayor precisión, la masa o la longitud?.
La medida de mayor precisión es la de la longitud porque se coge con una precisión de media centésima (de milímetro) mientras que la balanza ofrece una precisión de una décima (de gramo).
En realidad, ¿la balanza del laboratorio da la masa o el peso del objeto?. Si se hiciera el experimento en lo alto de una montaña, ¿cómo se vería afectado el resultado? ¿Por qué?
La balanza de laboratorio permite comparar las fuerzas (momentos de las fuerzas) que actúan sobre cada uno de los extremos. Esas fuerzas son la resultante de: el peso de platillos y cuerpos colocados sobre ellos menos el empuje de Arquímedes. Cuando la balanza está equilibrada podemos afirmar que el peso de los objetos colocados menos el empuje sobre ellos es igual en ambos extremos. Si se considera despreciable el empuje de Arquímedes sobre pesas y objeto (ya que la densidad del aire es pequeña y los cuerpos y pesas suelen ser pequeños) entonces podemos considerar que los pesos en ambos extremos son iguales.
Como la gravedad (g) es la misma para el cuerpo y las pesas se puede afirmar que las masas son iguales. Como la masa de las “pesas” es conocida queda determinada la masa del cuerpo.
Sin embargo, el peso de “las pesas” no es fijo pues depende de la gravedad del lugar y por consiguiente el peso no se determina directamente mediante la balanza sino mediante los dinamómetros. Resumiendo, una balanza de laboratorio mide masas mediante las comparaciones de sus pesos.
En lo alto de una montaña la medición de la masa no se vería afectada pues la variación de g (debida a la altura) afectaría en la misma proporción a los pesos de las pesas y al objeto.
PÉNDULO DE TORSIÓN
Objetivo de la práctica:
Determinar el módulo de torsión de una barra y el momento de inercia de una barra y de unas masas fijadas en ella.
Estudiar la dependencia del periodo de vibración de una barra con la longitud y la sección.
Calcular el módulo de rigidez de diferentes materiales: aluminio, acero,cobre y latón.
Material:
-
Disco graduado
-
Dinamómetro
-
Pesas
-
Barras de diferentes materiales y diferentes longitudes y secciones.
-
Cronómetro
-
Regla
Parte experimental:
1. Determinación del módulo de torsión
Se monta el dispositivo del péndulo de torsión, colocando en el centro una barra de aluminio de L = 500 mm y diámetro 2 mm. Se engancha el dinamómetro, previamente ajustado al cero, en uno de los pivotes extremos y se tira, manteniendo el dinamómetro perpendicular a la barra horizontal, ejerciendo una fuerza de 0.50 N. A continuación, se mide el ángulo girado por la barra y se repite la operación aplicando la misma fuerza en distintos pivotes. (Es conveniente ejercer fuerzas a ambos de la barra alternativamente con el fin de evitar deformaciones en un solo sentido).
i) Los resultados se muestran en la Tabla 1 (utilizando una barra de aluminio de medidas indicadas anteriormente)
Tabla 1: Ángulo girado por una barra de aluminio aplicando una fuerza constante a distintas distancias.
| Fuerza F (N) | Distancia d (mm) | Ángulo girado α (grados; °) |
| 0.50 | 150 | 68.0 |
| 0.50 | 125 | 55.0 |
| 0.50 | 100 | 45.0 |
| 0.50 | 75.0 | 35.0 |
| 0.50 | 50.0 | 20.0 |
** Los resultados se estudian en la Gráfica 1.
Gráfica 1: Ángulo girado en función del Momento aplicado. Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 1 y se calcula el momento de cada fuerza (se considera a M como variable “x” y a α como variable “y”)
| Momento M (N·mm) | Ángulo girado α (grados; °) |
| 69.5 | 68.0 |
| 51.2 | 55.0 |
| 35.4 | 45.0 |
| 21.5 | 35.0 |
| 8.55 | 20.0 |
ii) Se calculan los siguientes valores (siendo M≡x , α≡y)
∑ x = 186.15
∑ x2 = 9240.2025
∑ y = 223
∑ y2 = 11299
∑ x·y = 10058.5
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 3464.89875
σy = ∑ y2 - 1/N (∑ y)2 = 3010.83333
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 3139.925
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.76031739
n = [∑ y-m· ∑ x] / N = 16.29338356
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 11.47237285
s2m = 3.3110269·10-3
s2n = 1.912062142
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.994893235
** La ecuación de la recta será: y = 0.526140794· x + 8.411778229
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 5.00
P2* x = 65.0
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 11.0
y2 = 42.6
P1 (5.00, 11.0) P2 (65.0, 42.6)
Se marcan los puntos y se traza la recta que los une.
Módulo de torsión:
Para calcular el módulo de torsión aplicamos la Ley de Hooke (en la torsión, el ángulo girado es proporcional al momento del par aplicado) dada por la expresión:
α = (1/R)·M
Comparando esta ecuación con la ecuación de la recta se obtendrá el valor de R:
α= (1/R)·M
y = m·x + n
y≡α ; x≡M ; m≡(1/R)
0.53= 1/R
R ≈ 1.88·10-3 N·m
** Dentro del experimento de “Determinación del módulo de torsión”, se repite el proceso para barras de cobre y acero de 500 mm de longitud y 2 mm de radio.
ii) En la Tabla 2 se muestran los datos obtenidos para la barra de cobre.
Tabla 2: Ángulo girado por una barra de cobre aplicando una fuerza constante a distintas distancias.
| Fuerza F (N) | Distancia d (mm) | Ángulo girado α (grados; °) |
| 0.50 | 150 | 45.0 |
| 0.50 | 125 | 34.0 |
| 0.50 | 100 | 29.0 |
| 0.50 | 75.0 | 20.0 |
| 0.50 | 50.0 | 12.0 |
Los resultados se muestran en la Gráfica 2
iii) En la Tabla 3 se muestran los datos obtenidos para la barra de acero (ver Gráfica3)
Tabla 3: Ángulo girado por una barra de acero aplicando una fuerza constante a distintas distancias.
| Fuerza F (N) | Distancia d (mm) | Ángulo girado α (grados; °) |
| 0.50 | 150 | 25.0 |
| 0.50 | 125 | 16.0 |
| 0.50 | 100 | 12.0 |
| 0.50 | 75.0 | 10.0 |
| 0.50 | 50.0 | 6.0 |
Gráfica 3: Ángulo girado en función del Momento aplicado. Ajuste por mínimos cuadrados (barra de acero).
i) Se toman los datos necesarios de la Tabla 3 y se calcula el momento de cada fuerza (se considera a M como variable “x” y a α como variable “y”)
| Momento M (N·mm) | Ángulo girado α (grados; °) |
| 69.5 | 25.0 |
| 51.2 | 16.0 |
| 35.4 | 12.0 |
| 21.5 | 10.0 |
| 8.55 | 6.0 |
ii) Se calculan los siguientes valores (siendo M≡x , α≡y)
∑ x = 186.15
∑ x2 = 9240.2025
∑ y = 69.0
∑ y2 = 1161
∑ x·y = 3247.8
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 3464.89875
σy = ∑ y2 - 1/N (∑ y)2 = 367.5
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 1107.075
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.293929704
n = [∑ y-m· ∑ x] / N = 2.856997114
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 3.444201292
s2m = 9.940265331·10-4
s2n = 0.574033548
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.977617554
** La ecuación de la recta será: y = 0.293929704· x + 2.856997114
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 5.00
P2* x = 65.0
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 4.30
y2 = 22.0
P1 (5.00, 4.30) P2 (65.0, 22.0)
Se marcan los puntos y se traza la recta que los une.
Módulo de torsión:
Para calcular el módulo de torsión aplicamos la Ley de Hooke (en la torsión, el ángulo girado es proporcional al momento del par aplicado) dada por la expresión:
α = (1/R)·M
Comparando esta ecuación con la ecuación de la recta se obtendrá el valor de R:
α= (1/R)·M
y = m·x + n
y≡α ; x≡M ; m≡(1/R)
R = 1/m ; R = (1/0.293929704) ; R =3.40217 N·mm ⇒ R = 0.340217·10-3 N·m
2. Determinación del Módulo de rigidez (G).
Se calcula el módulo de rigidez G para las tres barras de diferentes materiales teniendo en cuenta la ecuación:
π·r4
R= ---------· G
2·L
Se utilizan los resultados del módulo de torsión obtenidos en el apartado anterior:
Barra de aluminio:
π·(1.0·10-3)4
1.315789·10-3 = ----------------· G
2 · 0.50
G = 418800404.4 N/m2 ; G ≈0.42 GPa
El valor del módulo de rigidez para el aluminio dado por la bibliografía es:
G = 26 GPa
Barra de cobre:
π·(1.0)4
1.88 · 10-3 = -------------· G
2.0·500
G = 598422710.5 N/m2 ; G≈0.6 GPa
El valor del módulo de rigidez para el aluminio dado por la bibliografía es:
G = 41 GPa
Barra de acero:
π·(1.0·10-3)4
3.40217·10-3 = -----------------· G
2· 0.50
G = 1082944571 N/ m2 ; G≈1.1 GPa
El valor del módulo de rigidez para el aluminio dado por la bibliografía es:
G = 80 GPa
3. Determinación del momento de inercia del péndulo de torsión.
Se monta el mismo dispositivo que en los apartados anteriores con la barra de
aluminio de 500 mm de longitud y 2 mm de diámetro.
Se determina el periodo de vibración del péndulo desviando la aguja del cero un pequeño ángulo y dejando que oscile. Debe tenerse en cuenta que el periodo de las oscilaciones no depende del ángulo desde el cual se pone a oscilar.
Se mide el tiempo que tarda en dar un determinado número de oscilaciones.
Se repite el proceso varias veces, desviando la aguja unas veces hacia un lado
y otras hacia otro y se toma el valor medio de los tiempos obtenidos.
Se determina el periodo del péndulo dividiendo el tiempo promedio por el
número de oscilaciones.
Nota: El periodo del péndulo disminuye de forma muy importante al aumentar el diámetro de la varilla haciendo muy difícil contar el número de oscilaciones. Para compensar este efecto se sitúan dos masas iguales en los extremos de la barra rectangular aumentando así el momento de inercia del péndulo y por tanto el periodo T.
Los resultados obtenidos se muestran en la Tabla 4. Se utiliza la barra de aluminio, descrita en el apartado i), y dos masas de 153.3 g (entre las cuales hay 350 mm de separación).
Tabla 4: Período del péndulo de torsión
| Número de Oscilaciones | Tiempo t (s) | Periodo T (s) |
| 20 | 45.70 | 2.29 |
| 20 | 45.84 | 2.29 |
| 20 | 45.48 | 2.27 |
| 20 | 45.82 | 2.29 |
| 20 | 45.54 | 2.28 |
| t = 45.68 | T = 2.28 |
A partir de los datos de la Tabla 4, y acudiendo a la ecuación T = 2·π·(I/R)1/2 se calcula el momento de inercia, I.
2.28 = 2·π·(I / 0.989345509·10-3) 1/2
(2.28)2 = (2·π)2· (I /0.989345509·10-3)
5.1984·0.989345509·10-3 = 4·π2 ·I
I = 1.302740587·10-4 kg·m2
Se comprueba si se cumple también I ≈ 2·m·d2
I = 2· 0.1533· (0.175)2
I = 9.389625·10-3 kg·m2
Los dos resultados difieren uno del otro seguramente a los posibles errores cometidos en los datos asociados a la parte experimental.
4. Dependencia de R con la geometría de las varillas.
Se toman barras de un mismo material (aluminio) pero con distintas dimensiones.
Tabla 5: Dependencia con la longitud
Con las barras de 2mm de diámetro y distintas longitudes L = 300, 400, 500 mm, se determina el periodo de oscilación como en el apartado anterior.
| Barra: L = 500 mm, φ= 2mm | Barra:L = 400 mm,φ =2mm | Barra: L = 300 mm, φ= 2mm | ||||||
| Número Oscilac. | Tiempo t (s) | Periodo T (s) | Número Oscilac. | Tiempo t (s) | Period. T (s) | Número Oscilac. | Tiempo t (s) | Periodo T (s) |
| 20 | 45.70 | 2.29 | 20 | 40.91 | 2.05 | 20 | 35.75 | 1.79 |
| 20 | 45.84 | 2.29 | 20 | 41.09 | 2.05 | 20 | 35.67 | 1.78 |
| 20 | 45.48 | 2.27 | 20 | 40.81 | 2.04 | 20 | 35.60 | 1.78 |
| 20 | 45.82 | 2.29 | 20 | 40.88 | 2.04 | 20 | 35.71 | 1.79 |
| 20 | 45.54 | 2.28 | 20 | 41.10 | 2.06 | 20 | 35.65 | 1.78 |
| Medias: | t =45.68 | T= 2.28 | Medias: | t=40.96 | T=2.05 | Medias: | t=35.68 | T=1.78 |
Tabla 6: Dependencia con la sección
Con las barras (de aluminio) de la misma longitud L = 500 mm y distintos diámetros φ = 2, 3, 4 mm se determina el periodo de oscilación como en el caso anterior.
| Barra: L = 500 mm, φ= 2mm | Barra:L = 500 mm,φ =3mm | Barra: L = 500 mm, φ= 4mm | ||||||
| Número Oscilac. | Tiempo t (s) | Periodo T (s) | Número Oscilac. | Tiempo T (s) | Period. T (s) | Número Oscilac. | Tiempo t (s) | Periodo T (s) |
| 20 | 45.70 | 2.29 | 20 | 21.12 | 1.06 | 20 | 6.52 | 0.33 |
| 20 | 45.84 | 2.29 | 20 | 21.02 | 1.05 | 20 | 6.49 | 0.32 |
| 20 | 45.48 | 2.27 | 20 | 21.06 | 1.05 | 20 | 6.41 | 0.32 |
| 20 | 45.82 | 2.29 | 20 | 21.11 | 1.06 | 20 | 6.46 | 0.32 |
| 20 | 45.54 | 2.28 | 20 | 21.09 | 1.05 | 20 | 6.41 | 0.32 |
| Medias: | t =45.68 | T= 2.28 | Medias: | t=21.08 | T=1.05 | Medias: | t= 6.46 | T=0.32 |
** Teniendo en cuenta la relación existente entre el periodo de vibración y la longitud de la barra por la ecuación T = 2·π· [(2·L·I)/( π·G)]1/2·r -2.
¿Qué se debería representar en cada eje para obtener una línea recta cuando se estudia la dependencia del periodo de vibración con la longitud de la barra T=T(L)? ¿Qué se debería representar en cada eje cuando se estudia la dependencia con el radio de la barra T=T(r)?
En ambos casos para conseguir una línea recta deben tomarse logaritmos en cada uno de los ejes.
FLEXIÓN DE UNA BARRA
Introducción y Objetivo:
Se quiere verificar la Ley de Hooke en el caso de la flexión de una barra y determinar el módulo de Young.
Según la Ley de Hooke, la deformación para un material elástico, dentro de los límites de elasticidad, es proporcional a la fuerza aplicada. Al flexionar una barra, ésta experimenta un alargamiento por su parte convexa y una contracción por la cóncava. Este comportamiento de la barra está determinado por el módulo de Young del material del que está hecha, de modo que el valor de dicho módulo puede determinarse por medio de experimentos de flexión.
Material:
-
Barras metálicas de distintas longitudes y secciones (1)
-
Reloj comparador (2)
-
Gancho cuelga pesas (3)
-
Juego de pesas (4)


Parte experimental:
Determinación del módulo de elasticidad de una barra:
Se sitúa una barra en posición horizontal, apoyada en sus extremos sobre las aristas de los soportes prismáticos separados a una distancia de aproximadamente 40 cm.
Se coloca el reloj comparador con su punta de medida en el centro de la barra apoyado sobre el fulcro con asa. La punta de medida ha de estar situada perpendicularmente a la barra.
Se desplaza verticalmente la barra hasta que el reloj comparador marque aproximadamente 0.00. Cabe señalar que el dial principal indica las centésimas de milímetro y el dial más pequeño cuenta los milímetros.
Se carga la barra incrementando de 50 en 50 g las masas apoyadas en el gancho portapesas.
Para cada una de las cargas colocadas se anota el desplazamiento del centro de la barra; este desplazamiento será s'.
Una vez obtenida una deformación suficiente, se va descargando la barra retirando las pesas y se miden los sucesivos desplazamientos; estos desplazamientos serán s''.
A continuación se calcula el valor promedio, s, para cada carga.
Tabla 1: Desplazamientos de la barra al adicionar o sustraer cargas
|
| S' (mm) | S'' (mm) | S'+ S'' S = --------- (mm) 2 | F (N) |
| 1ª | 0.1 | 0.7 | 0.4 | 4.9·10-1 |
| 2ª | 0.6 | 1.4 | 1.0 | 9.8·10-1 |
| 3ª | 1.3 | 2.1 | 1.7 | 15·10-1 |
| 4ª | 2.0 | 2.5 | 2.3 | 20·10-1 |
| 5ª | 2.7 | 3.3 | 3.0 | 25·10-1 |
| 6ª | 3.3 | 3.3 | 3.3 | 29·10-1 |
A partir de estos datos, se calcula el módulo de elasticidad de la barra según la ecuación siguiente:
S = ¼ (L/b)3·(1/a)·(1/E)· F
1.95 = ¼ (400/1.5) 3·(1/15)·(1/E)· 1.73
E = 280392.5293 N/mm2 ⇒ 2.803925293 ·1011 N/m2
E = 280.3925293 GPa ⇒ E ≈ 280 GPa
Se utiliza una barra de acero. Acudiendo a la bibliografía sobre este material se observa que:
| 280 - 206 |
E = 206 GPa ; % error = --------------------- x 100 = 35.9%
206
Gráfica 1: Desplazamiento en función de la Fuerza. Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 1(se considera a F como variable “x” y a S como variable “y”)
| S'+ S'' S = ------- (mm) 2 | F (N) |
| 0.4 | 4.9·10-1 |
| 1.0 | 9.8·10-1 |
| 1.7 | 15·10-1 |
| 2.3 | 20·10-1 |
| 3.0 | 25·10-1 |
| 3.3 | 29·10-1 |
ii) Se calculan los siguientes valores (siendo F≡x , S≡y)
∑ x = 10.37
∑ x2 = 22.1105
∑ y = 11.7
∑ y2 = 29.23
∑ x·y = 25.396
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 4.187683
σy = ∑ y2 - 1/N (∑ y)2 = 6.415
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 5.1745
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 1.2356475
n = [∑ y-m· ∑ x] / N = - 0.1856108
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 5.285512·10-3
s2m = 1.262157·10-3
s2n = 8.809187·10-4
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.998351
** La ecuación de la recta será: y = 1.2356475 · x - 0.1856108
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 4.0·10-1
P2* x = 28·10-1
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.3
y2 = 3.3
P1 (4.0·10-1, 0.3) P2 (28·10-1, 3.3)
Se marcan los puntos y se traza la recta que los une.
Influencia de la geometría de la barra en la constante elástica
Se quiere estudiar la dependencia de la constante de la ley de Hooke con la geometría de las barras. Se aplicará una fuerza constante (un peso fijo de 160 g) y se medirá el desplazamiento, s, que experimentan las distintas barras.
Igual que el experimento anterior pero con F constante. Se construirá una tabla con distintas barras.
a: ancho
b: espesor
L: longitud
Tabla 2: Desplazamiento de barras de igual longitud y distintos valores de espesor y anchura (con Fuerza constante).
| F (N) | L (mm) | a (mm) | b (mm) | S (mm) |
| 1.57 | 385 | 10.0 | 1.50 | 2.60 |
| 1.57 | 385 | 15.0 | 1.50 | 1.70 |
| 1.57 | 385 | 20.0 | 1.50 | 1.40 |
| 1.57 | 385 | 10.0 | 2.00 | 1.20 |
| 1.57 | 385 | 10.0 | 3.00 | 0.30 |
Tabla 3: Desplazamiento de barras de distintas longitudes e iguales valores de espesor y anchura (con Fuerza constante).
| F (N) | L (mm) | a (mm) | b (mm) | S (mm) |
| 1.57 | 460 | 10.0 | 2.00 | 1.60 |
| 1.57 | 385 | 10.0 | 2.00 | 1.20 |
| 1.57 | 300 | 10.0 | 2.00 | 0.40 |
Gráfica 4: Desplazamiento en función de la Longitud de la barra (con Fuerza constante). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 3(se considera a log L como variable “x” y a log S como variable “y”)
| L (mm) | S (mm) | Log L | Log S |
| 460 | 1.60 | 2.66 | 0.20 |
| 385 | 1.20 | 2.59 | 0.08 |
| 300 | 0.40 | 2.48 | -0.40 |
ii) Se calculan los siguientes valores (siendo Log L≡x , Log S≡y)
∑ x = 7.73
∑ x2 = 19.9341
∑ y = -0.12
∑ y2 = 0.2064
∑ x·y = -0.2528
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = -9.975283
σy = ∑ y2 - 1/N (∑ y)2 = 0.204
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = -0.0982
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 3.425101187
n = [∑ y-m· ∑ x] / N = - 8.865344058
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 0.051241678
s2m = - 5.136864624·10-3
s2n = 8.540279667·10-3
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.978883461
** La ecuación de la recta será: y = 3.425101187 · x - 8.865344058
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 2.45
P2* x = 2.65
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = -0.47
y2 = 0.21
P1 (2.45, -0.47) P2 (2.65, 0.21)
Se marcan los puntos y se traza la recta que los une.
Gráfica 2: Desplazamiento en función de la anchura de la barra (con Fuerza, longitud y espesor constantes). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 2(se considera a log a como variable “x” y a log S como variable “y”)
| a (mm) | S (mm) | Log a | Log S |
| 10.0 | 2.60 | 1.00 | 0.42 |
| 15.0 | 1.70 | 1.18 | 0.23 |
| 20.0 | 1.40 | 1.30 | 0.15 |
ii) Se calculan los siguientes valores (siendo Log a≡x , Log S≡y)
∑ x = 3.48
∑ x2 = 4.0824
∑ y = 0.80
∑ y2 = 0.2518
∑ x·y = 0.8864
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 2.064
σy = ∑ y2 - 1/N (∑ y)2 = 0.14513
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 0.4224
iv) Los parámetros de ajuste serán:
m = σx·y /σx = -0.912280701
n = [∑ y-m· ∑ x] / N = 1.324912281
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 0.014671337
s2m = 7.108206012·10-3
s2n = 2.445222833·10-3
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = -0.993273004
** La ecuación de la recta será: y = -0.912280701 · x - 1.324912281
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 0.90
P2* x = 1.40
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.50
y2 = 0.05
P1 (0.90, 0.50) P2 (1.40, 0.05)
Se marcan los puntos y se traza la recta que los une.
Gráfica 3: Desplazamiento en función del espesor de la barra (con Fuerza, Longitud y anchura constantes). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 2(se considera a log b como variable “x” y a log S como variable “y”)
| b (mm) | S (mm) | Log b | Log S |
| 1.50 | 2.60 | 0.18 | 0.41 |
| 2.00 | 1.20 | 0.30 | 0.08 |
| 3.00 | 0.30 | 0.48 | -0.52 |
ii) Se calculan los siguientes valores (siendo Log b≡x , Log S≡y)
∑ x = 0.96
∑ x2 = 0.3528
∑ y = -0.03
∑ y2 = 0.4449
∑ x·y = -0.1518
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 0.1992
σy = ∑ y2 - 1/N (∑ y)2 = -0.44475
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = -0.147
iv) Los parámetros de ajuste serán:
m = σx·y /σx = -3.118421053
n = [∑ y-m· ∑ x] / N = 0.987894736
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = -0.138307228
s2m = - 0.694313398
s2n = - 0.023051204
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = -0.998694011
** La ecuación de la recta será: y = -3.118421053 · x + 0.987894736
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 0.51
P2* x = 0.15
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = -0.60
y2 = 0.52
P1 (0.51, -0.60) P2 (0.15, 0.52)
Se marcan los puntos y se traza la recta que los une.
Para linealizar una ecuación, además de tomar logaritmos, se puede tomar:
Representar “y” frente a la inversa de “x”
Representar “ y2 ” frente a “x”
Representar “ln y” frente a “x”
* Las ventajas de estos métodos radica en que siempre es más sencillo estudiar los resultados obtenidos mediante una recta que mediante otro tipo de función.
* Los inconvenientes pueden estar en la representación de ciertos valores; por ejemplo:
-
Para un valor y = 0 se obtendría log y ó ln y = ∞ [en el caso de tomar logaritmos y en la expresión iii)]
-
Para un valor x = 0 se obtiene un valor de (1/x) = ∞ [en la expresión i)]
Cuestiones relativas a la práctica
El reloj comparador utilizado tiene una sensibilidad de 0.01 mm sin embargo, las centésimas de milímetro en estas medidas no son significativas y se han retenido sólo las décimas. Explíquese la razón.
Como el grosor de la barra se considera hasta las décimas, el desplazamiento sólo tiene sentido expresarlo hasta las décimas también, ya que las centésimas son despreciables e insignificativas.
¿Es perfectamente elástica la deformación que experimenta la barra cuando se carga con diferentes pesos?. Justifíquese.
Es posible que la varilla no recobre su estado inicial después del proceso de medida, esto indica que se ha rebasado el límite de elasticidad por haberla cargado excesivamente, por lo que la varilla ha experimentado una deformación permanente.
En una barra rectangular como la que se ha utilizado en esta práctica, ¿qué dimensión tiene más influencia sobre la flecha de flexión, el ancho de la barra o su grosor?.
Observando los resultados obtenidos en la Tabla 2, se puede apreciar que la dimensión que ejerce mayor influencia en la flecha de flexión es el grosor de la barra.
DINÁMICA DE ROTACIÓN
Introducción y Objetivo:
Cuando en un movimiento todos los puntos de un cuerpo describen trayectorias circulares respecto a un eje común, se dice que el cuerpo está sometido a un movimiento de rotación y un punto particular se mueve con movimiento circular. La característica de este movimiento es el cociente entre el ángulo descrito y el tiempo invertido en ello y se denomina velocidad angular (con unidades rad/s). Si la velocidad angular es constante con el tiempo, se dice que el movimiento circular es uniforme.
Por otro lado, si la velocidad angular varía con el tiempo, se dice que el movimiento es circular acelerado. En esta situación, el cociente entre el incremento de la velocidad angular y el tiempo empleado en la variación se denomina aceleración angular. (con unidades rad/s2 ). Si la aceleración angular es constante, el movimiento se denomina movimiento circular uniformemente acelerado.
El objetivo de esta práctica es el estudio del movimiento circular uniformemente acelerado. Velocidad angular, aceleración angular, momento de inercia.
Material:
-
Dispositivo experimental con soportes de acoplamiento
-
Disco metálico graduado
-
Ventilador
-
Célula fotoeléctrica
-
Dos contadores P
-
Cable disparador
-
Nivel de burbuja
-
Pesas variadas


Parte experimental:
Estudio de la velocidad angular en función del tiempo.
En la Tabla 1 se muestran los valores de t1, Δt, y φ. A partir de los resultados obtenidos, se calcularán los valores de ω y t.
Tabla 1: Valores de t1 y Δt para diferentes ángulos φ y una masa de 20g y un radio de giro r=1.5 cm (a partir de t1 y Δt se calcula t y ω)
| Ángulo φ | Masa m (g) | Radio de giro r (cm) | t1 (s) | Δt (s) | Tiempo t (s) | Velocidad angular ω (rad/s) |
| 60º | 20 | 1.5 | 4.386 | 0.659 | 4.716 | 0.222 |
| 90º | 20 | 1.5 | 5.071 | 0.536 | 5.339 | 0.294 |
| 120º | 20 | 1.5 | 5.412 | 0.430 | 5.627 | 0.372 |
| 180º | 20 | 1.5 | 7.053 | 0.375 | 7.241 | 0.434 |
| 270º | 20 | 1.5 | 9.484 | 0.278 | 9.623 | 0.490 |
Para calcular el tiempo, t, se utiliza la siguiente expresión:
t = t1 + Δt/2
Para 60º : t = 4.386 + (0.659/2) = 4.716 s ; 60º = π/3 rad
Para 90º : t = 5.071 + (0.536/2) = 5.339 s ; 90º = π/2 rad
Para 120º: t = 5.412 + (0.430/2) = 5.627 s ; 120º = (2π)/3 rad
Para 180º: t = 7.053 + (0.375/2) = 7.241 s ; 180º = π rad
Para 270º: t = 9.484 + (0.278/2) = 9.623 s ; 270º = (3π)/2 rad
Gráfica 1: Velocidad angular (ω) en función del tiempo (t). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 1 (se considera a “t” como variable “x” y a “ω” como variable “y”)
| Tiempo t(s) | Velocidad angular ω (rad/s) |
| 4.716 | 0.222 |
| 5.339 | 0.294 |
| 5.627 | 0.372 |
| 7.241 | 0.434 |
| 9.623 | 0.490 |
ii) Se calculan los siguientes valores (siendo t≡x , ω≡y)
∑ x = 32.546
∑ x2 = 227.442916
∑ y = 1.812
∑ y2 = 0.70256
∑ x·y = 12.567726
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 15.5944928
σy = ∑ y2 - 1/N (∑ y)2 = 0.0458912
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 0.7730556
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.049572346
n = [∑ y-m· ∑ x] / N = 0.039723682
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 2.523006654 · 10-3
s2m = 1.617883112 · 10-4
s2n = 5.046013308 · 10-3
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.913819447
** La ecuación de la recta será: y = 0.049572346· x + 0.039723682
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 3.000
P2* x = 10.00
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.188
y2 = 0.535
P1 (3.000, 0.188) P2 (10.00, 0.535)
Se marcan los puntos y se traza la recta que los une.
Teniendo en cuenta la ecuación ω(t) = α · t y teniendo en cuenta que t≡x , ω≡y; por similitud con la ecuación de la recta obtenida (y= m·x + n) se deduce que la pendiente (m) es la aceleración angular (α). Así pues:
α = 0.050 rad/s2
m·g·r
Además, conociendo la ecuación ω(t) = α · t = ----------- · t ,
Iz
se puede calcular el momento de inercia del sistema.
0.02 kg · 9.8 m/s · 0.015 m
0.050 rad/s2 · t = --------------------------------------- · t
Iz
2.94 ·10-3 (kg·m2·s-2)
Iz = -------------------------------- = 0.059 kg·m2
0.050 rad/ s2
Iz= 0.059 kg·m2
Dependencia de la aceleración angular (α) con la fuerza (F).
Se procede de forma análoga al punto 1. Se calcula mediante un método gráfico los valores de α (es la pendiente de la recta obtenida al representar ω frente a t) para un mismo radio r = 1.5 cm y distintos valores de la masa, m (m = 20 g, 40g y 60 g).
Para la masa m= 20g, se toman los valores obtenidos en el punto 1 (Tabla 1 y Gráfica 1) (α = 0.050 rad/s2).
Tabla 2: Valores de t1 y Δt para diferentes ángulos φ y una masa de 40g y un radio de giro r=1.5 cm (a partir de t1 y Δt se calcula t y ω).
| Ángulo φ | Masa m (g) | Radio de giro r (cm) | t1 (s) | Δt (s) | Tiempo t (s) | Velocidad angular ω (rad/s) |
| 60º | 40 | 1.5 | 2.582 | 0.348 | 2.756 | 0.380 |
| 90º | 40 | 1.5 | 3.070 | 0.273 | 3.201 | 0.491 |
| 120º | 40 | 1.5 | 3.559 | 0.238 | 3.678 | 0.569 |
| 180º | 40 | 1.5 | 4.161 | 0.195 | 4.259 | 0.738 |
| 270º | 40 | 1.5 | 5.523 | 0.170 | 5.608 | 0.840 |
Para calcular el tiempo, t, se utiliza la siguiente expresión:
t = t1 + Δt/2
Para 60º : t = 2.582 + (0.348/2) = 2.756 s ; 60º = π/3 rad
Para 90º : t = 3.070 + (0.273/2) = 3.201 s ; 90º = π/2 rad
Para 120º: t = 3.559 + (0.238/2) = 3.678 s ; 120º = (2π)/3 rad
Para 180º: t = 4.161 + (0.195/2) = 4.259 s ; 180º = π rad
Para 270º: t = 5.523 + (0.170/2) = 5.608 s ; 270º = (3π)/2 rad
Gráfica 2: Velocidad angular (ω) en función del tiempo (t). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 2 (se considera a “t” como variable “x” y a “ω” como variable “y”)
| Tiempo t(s) | Velocidad angular ω (rad/s) |
| 2.756 | 0.380 |
| 3.201 | 0.491 |
| 3.678 | 0.569 |
| 4.259 | 0.738 |
| 5.608 | 0.840 |
ii) Se calculan los siguientes valores (siendo t≡x , ω≡y)
∑ x = 19.502
∑ x2 = 80.958366
∑ y = 3.018
∑ y2 = 1.959486
∑ x·y = 12.565615
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 4.8927652
σy = ∑ y2 - 1/N (∑ y)2 = 0.1378212
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 0.7942078
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.162322892
n = [∑ y-m· ∑ x] / N = -0.02952421
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 2.967697531 · 10-3
s2m = 6.065481194 · 10-4
s2n = 5.935395062 · 10-4
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.967161381
** La ecuación de la recta será: y = 0.162322892· x - 0.02952421
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 2.000
P2* x = 5.000
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.295
y2 = 0.782
P1 (2.000, 0.295) P2 (5.000, 0.782)
Se marcan los puntos y se traza la recta que los une.
Teniendo en cuenta la ecuación ω(t) = α · t y teniendo en cuenta que t≡x , ω≡y; por similitud con la ecuación de la recta obtenida (y= m·x + n) se deduce que la pendiente (m) es la aceleración angular (α). Así pues:
α = 0.160 rad/s2
Tabla 3: Valores de t1 y Δt para diferentes ángulos φ y una masa de 60g y un radio de giro r=1.5 cm (a partir de t1 y Δt se calcula t y ω).
| Ángulo φ | Masa m (g) | Radio de giro r (cm) | t1 (s) | Δt (s) | Tiempo t (s) | Velocidad angular ω (rad/s) |
| 60º | 60 | 1.5 | 2.302 | 0.298 | 2.451 | 0.427 |
| 90º | 60 | 1.5 | 2.391 | 0.205 | 2.494 | 0.630 |
| 120º | 60 | 1.5 | 2.701 | 0.176 | 2.789 | 0.751 |
| 180º | 60 | 1.5 | 3.368 | 0.150 | 3.443 | 0.912 |
| 270º | 60 | 1.5 | 4.140 | 0.125 | 4.203 | 1.121 |
Para calcular el tiempo, t, se utiliza la siguiente expresión:
t = t1 + Δt/2
Para 60º : t = 2.302 + (0.298/2) = 2.451 s ; 60º = π/3 rad
Para 90º : t = 2.391 + (0.205/2) = 2.494 s ; 90º = π/2 rad
Para 120º: t = 2.701 + (0.176/2) = 2.789 s ; 120º = (2π)/3 rad
Para 180º: t = 3.368 + (0.150/2) = 3.443 s ; 180º = π rad
Para 270º: t = 4.140 + (0.125/2) = 4.203 s ; 270º = (3π)/2 rad
Gráfica 3: Velocidad angular (ω) en función del tiempo (t). Ajuste por mínimos cuadrados
i) Se toman los datos necesarios de la Tabla 3 (se considera a “t” como variable “x” y a “ω” como variable “y”)
| Tiempo t(s) | Velocidad angular ω (rad/s) |
| 2.451 | 0.427 |
| 2.494 | 0.630 |
| 2.789 | 0.751 |
| 3.443 | 0.912 |
| 4.203 | 1.121 |
ii) Se calculan los siguientes valores (siendo t≡x , ω≡y)
∑ x = 15.38
∑ x2 = 49.525416
∑ y = 3.841
∑ y2 = 3.231615
∑ x·y = 12.563915
iii) A continuación:
σx = ∑ x2 - 1/N (∑ x)2 = 2.216536
σy = ∑ y2 - 1/N (∑ y)2 = 0.2809588
σx·y = ∑ x·y - 1/N (∑ x) (∑ y) = 0.748999
iv) Los parámetros de ajuste serán:
m = σx·y /σx = 0.337914204
n = [∑ y-m· ∑ x] / N = -0.271224094
v)Las varianzas serán:
s2m = s2y /σx
s2n = s2y/N , siendo s2y = 1/(N-2) · [σy -(σ2xy/σx)] = 9.287132823 · 10-3
s2m =4.189930966 · 10-3
s2n = 1.857426565 · 10-3
vi) El coeficiente de correlación lineal será:
r = σxy/ (σx · σy)1/2
r = 0.949123056
** La ecuación de la recta será: y = 0.337914204· x - 0.271224094
Para trazar la recta de ajuste:
Se toman las coordenadas de dos puntos espaciados
P1* x = 2.000
P2* x = 4.000
Sustituyendo en la ecuación de la recta se obtienen los valores de y:
y1 = 0.405
y2 = 1.080
P1 (2.000, 0.405) P2 (4.000, 1.080)
Se marcan los puntos y se traza la recta que los une.
Teniendo en cuenta la ecuación ω(t) = α · t y teniendo en cuenta que t≡x , ω≡y; por similitud con la ecuación de la recta obtenida (y= m·x + n) se deduce que la pendiente (m) es la aceleración angular (α). Así pues:
α = 0.338 rad/s2
Tabla 4: Aceleraciones angulares (α) y Fuerzas (F) correspondientes a cada una de las masas
| Masa (g) | Aceleración angular (α) (rad/s2) | Fuerza (N) |
| 20 | 0.050 | 0.196 |
| 40 | 0.160 | 0.392 |
| 60 | 0.338 | 0.588 |
********Trazar........¿tipo Curva?
LEYES DE LOS CHOQUES
Introducción y Objetivo:
En esta práctica se estudiará la conservación del ímpetu o momento lineal y de la energía en diferentes tipos de colisiones.
La conservación del momento lineal (p= m·v) es un concepto físico muy importante. Sin embargo, este experimento es difícil de realizar en un laboratorio físico debido a la influencia de las fuerzas de rozamiento.
Un carril neumático es uno de los mejores métodos para investigar el momento lineal. Unos “coches” o planeadores de aluminio deslizando sobre una corriente de aire que sale del carril, elimina las fuerzas de rozamiento, condición indispensable para la conservación del momento lineal o ímpetu.
En ausencia de rozamiento y otras fuerzas externas, el momento lineal de un sistema de dos planeadores se conservará durante la colisión de los dos planeadores. Gracias a este montaje, el momento lineal total del sistema será el mismo antes y después del choque. Midiendo las velocidades de los “coches” de iguales y de diferentes masas antes y después de la colisión, y así se puede investigar la conservación del ímpetu. Además, si el choque es perfectamente elástico, toda la energía acumulada durante la deformación de los cuerpos se recupera cuando vuelven a su forma original. Las energías cinéticas antes y después del choque son iguales.
Material:
-
Carril neumático de 2m de largo
-
Soplador eléctrico
-
Dos fotopuertas
-
Ordenador Apple Macintosh
-
Interfaz MacTimer
-
Dos planeadores de aluminio anodizado, con una masa de 180±1 g
-
Cuatro pesas de 50 g para los planeadores
-
Dos banderas de 100 mm de largo
-
Dos bandas de gomaparachoques
-
Lámina parachoques
-
Tubo con ceera
-
Aguja
Descargar
| Enviado por: | Vicente |
| Idioma: | castellano |
| País: | España |
