Matemáticas
Estadística descriptiva
INTRODUCCION
-
El presente trabajo de Estadística Descriptiva reúne un estudio descriptivo a la recopilación, organización y representación de los datos estadísticos en la que se tomó como muestra la población estudiantil del Colegio Centro Social Bachillerato Nocturno, para clasificarlo según sus edades.
-
Luego se introducen algunos procedimientos tales como las medidas matemáticas y no matemáticas de tendencia central, las medidas de dispersión absoluta y relativa con el fin de sintetizar la información.
-
Finalmente se hace un breve estudio sobre la regresión y correlación, los cuales nos ayudan a hacer predicciones en eventos futuros con base en los datos actuales.
OBJETIVOS
Describir estadísticamente la información recopilada para esta investigación.
Conocer de que forma se puede medir las tendencias matemáticas y no matemáticas.
Saber como se mide el grado de variabilidad de los datos.
Ver como se pueden medir los cambios que sufren en el tiempo algunas variaciones como precios, cantidades y valores.
METODOLGIA
El presente trabajo se realiza bajo el ámbito de un estudio estadístico acerca de las edades de los estudiantes del Colegio Centro Social Bachillerato Nocturno, tomándose una muestra de 70 alumnos entre hombre y mujeres, con el fin de determinar cuales son los promedios oscilantes de edades en que se encuentra la población estudiantil de dicho plantel educativo.
JUSTIFICACION
Este estudio se realizó con el fin de adquirir un mayor conocimiento y precisión los datos estadísticos.
DE LA POBLACION ESTUDIANTIL DEL COLEGIO CENTRO SOCIAL BACHILLERATO NOCTURNO, SE TOMO UNA MUESTRA DE 70 ALUMNOS Y SE DESEA CLASIFICAR SEGÚN SUS EDADES ASÍ:
| Y1 | 20 | 11 | 39 | 36 | 39 | 30 | 13 |
| Y2 | 21 | 30 | 31 | 32 | 49 | 21 | 26 |
| Y3 | 18 | 47 | 33 | 24 | 44 | 18 | 29 |
| Y4 | 17 | 42 | 35 | 21 | 38 | 14 | 35 |
| Y5 | 19 | 39 | 17 | 19 | 17 | 42 | 48 |
| Y6 | 15 | 32 | 19 | 17 | 53 | 34 | 17 |
| Y7 | 14 | 19 | 40 | 11 | 13 | 26 | 16 |
| Y8 | 12 | 14 | 41 | 19 | 18 | 21 | 12 |
| Y9 | 15 | 11 | 13 | 16 | 14 | 19 | 21 |
| Y10 | 16 | 18 | 44 | 14 | 15 | 12 | 23 |
CLASIFICAR LOS DATOS EN SEIS INTERVALOS (M)
VARIABLE: LA VARIABLE ES CONTINUA
RECORRIDO : R = Dm - dm
R = 53-11
R = 42
AMPLITUD = R/M
A= 42/6 = 7
A = 7
La amplitud indica la distancia que debe tener cada grupo. para formar los de clase, se parte del dato menor 11 y se le suma la amplitud 7.
MARCA DE CLASE
| J | Y' j-1 - Y | Numero de estudiantes | total |
| 1 | 11 - 18 | / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / | 30 |
| 2 | 18 - 25 | / / / / / / / / / / / / / / | 14 |
| 3 | 25 - 32 | / / / / / / / / | 8 |
| 4 | 32 - 39 | / / / / / / / / / | 9 |
| 5 | 39 - 46 | / / / / / / | 6 |
| 6 | 46 - 53 | / / / | 3 |
DISTRIBUCION DE FRECUENCIAS
| ORDEN DE LA CLASE | INTERVALO DE CLASE | MARCA DE CLASE | FRECUENCIA ABSOLUTA | FRECUENCIA RELATIVA | ACUMULADAS | |||
| ABSOLUTAS | RELATIVAS | |||||||
| j | Y'j-1 - Y'j | Yj | nj | hj | ! Nj | ! Nj | ! Hj | ! Hj |
| 1 | 11 - 18 | 14.5 | 30 | 0.43 | 30 | 70 | 0.43 | 1.00 |
| 2 | 18 - 25 | 21.5 | 14 | 0.20 | 44 | 40 | 0.63 | 0.57 |
| 3 | 25 - 32 | 28.5 | 8 | 0.11 | 52 | 26 | 0.74 | 0.37 |
| 4 | 32 - 39 | 35.5 | 9 | 0.13 | 61 | 18 | 0.87 | 0.26 |
| 5 | 39 - 46 | 42.5 | 6 | 0.09 | 67 | 9 | 0.96 | 0.13 |
| 6 | 46 - 53 | 49.5 | 3 | 0.04 | 70 | 3 | 1.00 | 0.04 |
| TOTAL | 70 | |||||||
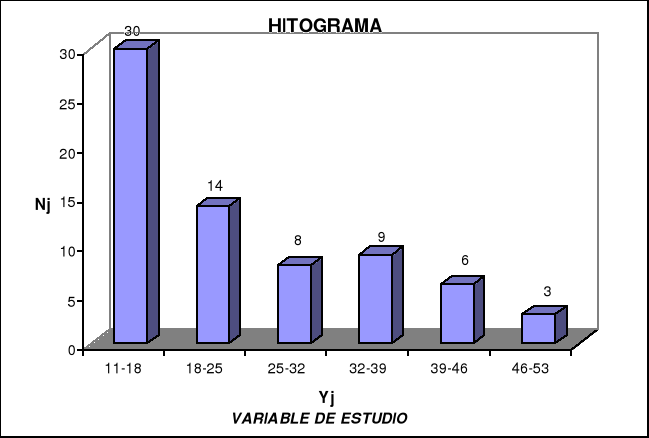
En el histograma está representado gráficamente una distribución de frecuencias con intervalos de amplitud.
Este polígono de frecuencias esta representado en una curva la tendencia de la información objeto de este estudio, señalando la concentración de la información.
La ojiva nos muestra la forma como crece y decrece la información a través de los intervalos. Para realizar la gráfica se tuvo en cuenta las frecuencias acumuladas (absoluta y relativa) en forma ascendente y descendente.
MEDIDAS MATEMATICAS
MEDIA ARITMETICA
| Yj | nj | Yj * nj Total del clase |
| 14.5 | 30 | 435.00 |
| 21.5 | 14 | 301.00 |
| 28.5 | 8 | 228.00 |
| 35.5 | 9 | 319.50 |
| 42.5 | 6 | 255.00 |
| 49.5 | 3 | 148.50 |
| 70 | 1,687.00 |
MEDIA GEOMETRICA
La media geométrica G(X) de un conjunto de n valores es la raíz enésima del producto de las observaciones.
![]()
![]()
MEDIDAS NO MATEMATICAS
MEDIANA
| Y'j-1 - Y'j | nj | ! Nj |
| 11 - 18 | 30 | 30 |
| 18 - 25 | 14 | 44 |
| 25 - 32 | 8 | 52 |
| 32 - 39 | 9 | 61 |
| 39 - 46 | 6 | 67 |
| 46 - 53 | 3 | 70 |
La mediana es = 20.5
PERCENTILES
| J | Y'j-1 - Y'j | nj | ! Nj |
| 1 | 11 - 18 | 30 | 30 |
| 2 | 18 - 25 | 14 | 44 |
| 3 | 25 - 32 | 8 | 52 |
| 4 | 32 - 39 | 9 | 61 |
| 5 | 39 - 46 | 6 | 67 |
| 6 | 46 - 53 | 3 | 70 |
| 70 |
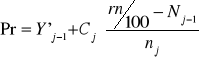
r = partes tomadas
n = Tamaño de la muestra (total de observaciones)
![]()
, corresponden al 68% de alumnos
![]()
alumnos
Esta cantidad indica que el 68% de los 70 alumnos tienen una edad máxima de 28.15 años y el 32% restante supera esta edad.
MODA
Moda es el valor de la variable que se repite con más frecuencia.
Notación: Md(X)
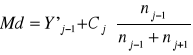
Donde: Md = Moda
Y'j-1 = Limite de la clase modal
Cj = Amplitud de clase
nj-1 = Frecuencia anterior a la más lata frecuencia
nj = Frecuencia más alta
nj+1 = Frecuencia posterior a la más alta frecuencia
| Y'j-1 - Y'j | nj |
| 11 - 18 | 30 |
| 18 - 25 | 14 |
| 25 - 32 | 8 |
| 32 - 39 | 9 |
| 39 - 46 | 6 |
| 46 - 53 | 3 |
![]()
alumnos
MEDIDAS DE DISPERSION
MEDIDAS DE DISPERSION ABSOLUTA
La dispersión se puede medir en términos de distancia (diferencial) entre los valores de un conjunto de datos y se considera una medida de referencia de ese mismo conjunto.
EL RANGO O RECORRIDO
Es la diferencia entre el dato mayor y el dato menor de los valores observados en la variable de estudio.
R = Rango
D = Valor de la observación mayor
d = Valor de la observación menor
El rango no analiza sino los datos extremos y no la variación de todo el conjunto de datos
R = D - d
R = 53 - 11
R = 42
Este valor indica la distancia que existe entre la edad mayor y la edad menor.
B) EL RANGO MODIFICADO
| Y'j-1 - Y'j | Nj | ! Nj |
| 11 - 18 | 30 | 30 |
| 18 - 25 | 14 | 44 |
| 25 - 32 | 8 | 52 |
| 32 - 39 | 9 | 61 |
| 39 - 46 | 6 | 67 |
| 46 - 53 | 3 | 70 |
| 70 |
R50
R40
0% P11 P20 P25 P55 P60 P65 70%
R60
70%
R = Rango
P60 = Percentil 60
P20 = Percentil 10
![]()
alumnos
![]()
alumnos
VARIANZA
Nos indica la distancia promedio de cualquier observación en el conjunto de datos

S2 = Varianza de la muestra
Xj = Observación i de la muestra
![]()
= Promedio de la muestra
N = Tamaño de la muestra
| Edades | Desviación con respecto a la media | Desviación elevada al cuadrado | |
| X | "(Xi - | "(Xi - | |
| 11 | 11 - 28.5 = | -17.5 | 306.25 |
| 18 | 18 - 28.5 = | -10.5 | 110.25 |
| 25 | 25 - 28.5 = | -3.5 | 12.25 |
| 32 | 32 - 28.5 = | 3.5 | 12.25 |
| 39 | 39 - 28.5 = | 10.5 | 110.25 |
| 46 | 46 - 28.5 = | 17.5 | 306.25 |
| 171 | 0 | 857.5 | |
Se calcula la media aritmética

La varianza con base en la definición es:

DESVIACION ESTANDAR
Se obtiene extrayendo la raíz cuadrada de la varianza
![]()
Este valor significa que los datos en promedio se alejan de la media aritmética en 11.95 años es decir la dispersión promedio:

REGRESION Y CORRELACION
REGRESION SIMPLE
El rector del Colegio Centro Social Bachillerato nocturno establece una relación entre la edad de los alumnos y las fallas a clases que tuvieron durante el año lectivo de 1998. Para esto recogió la muestra de 10 alumnos tomados al azar entre todos los alumnos que terminaron el año.
| Edad (X) | 25 | 19 | 17 | 23 | 21 | 16 | 25 | 31 | 39 | 28 |
| Fallas(Y) | 5 | 3 | 1 | 8 | 4 | 9 | 2 | 7 | 6 | 12 |
En el Colegio Centro Social se obtiene
| X | Y | XY | X2 | Y2 |
| 25 | 5 | 125 | 625 | 25 |
| 19 | 3 | 57 | 361 | 9 |
| 17 | 1 | 17 | 289 | 1 |
| 23 | 8 | 184 | 529 | 64 |
| 21 | 4 | 84 | 441 | 16 |
| 16 | 9 | 144 | 256 | 81 |
| 25 | 2 | 50 | 625 | 4 |
| 31 | 7 | 217 | 961 | 49 |
| 39 | 6 | 234 | 1521 | 36 |
| 28 | 12 | 336 | 784 | 144 |
| 244 | 57 | 1448 | 6392 | 429 |
![]()
![]()
Y = 2.828 - 0.130X
El Rector del colegio desea estimar las fallas de un alumno con 27 años de edad:
Y = 2.828 - 0.130*27 = 9.93
Se estima que un alumno de 27 años de edad falte a clases 9.93 veces.
La información gráficamente quedaría:
ERROR DE ESTIMACION

Error de estimación es = 3.15



![]()
![]()
Y1=(11+18)/2=14.5
N = 70
Nj-1 " n/2 < N'j
44 " 35 < 44

![]()

Descargar
| Enviado por: | Mendoza Cely Fredy Ignacio |
| Idioma: | castellano |
| País: | España |
