Filosofía y Ciencia
Eratóstenes
“Año de la consolidación democrática”
Institución educativa particular
“De La Cruz”
Trabajo de investigación individual
ERASTÓTENES
Ica-2006
“Año de la consolidación democrática”
Institución educativa particular
“De La Cruz”
Trabajo de investigación individual
ERASTÓTENES
Ica-2006
INDICE
Introducción.................................................................................5
Capitulo I……………………………………………………………….6
| |
Biografía………………………………………………………...7
Capitulo II………………………………………………………………8
Aportes…………………………………………………………9
Medición de la tierra…………………………………...9
Medición del sol con respecto a la luna…….............12
Compilación de estrellas……………………………...12
Sobre la geometría y geografía………………………13
Criba de Erastótenes…………………………….........14
Conclusiones………………………………………………………….16
Bibliografía……………………………………………………..............17
Anexos………………………………………………………………….18
Vocabulario Matemático……………………………………....19
INTRODUCCIÓN
Eratóstenes fue un hombre que hizo descubrimientos importantes que ayudaron descifrar los enigmáticos misterios que en ese momento rodearon a la ciencia, como la medición de la tierra y la distancia que el sol tenía en relación a la luna.
Sus aportes, a lo largo de estos años, han sido de mucha utilidad, ya que a él le debemos el conocimiento de los números primos uno de los pilares de la matemática que nos permite resolver una serie de problemas.
A lo largo de este trabajo hablaremos sobre quién fue Eratóstenes y los aportes que dejó a la historia y de la cual hoy podemos disfrutar.
Capitulo I
BIOGRAFÍA

Eratóstenes nació en Cyrene (Libia) en el año 276 a. C. Fue astrónomo, historiador, geógrafo, filósofo, poeta, crítico teatral y matemático. Estudió en Alejandría y Atenas. Alrededor del año 255 a. C fue el tercer director de la Biblioteca de Alejandría. Trabajó con problemas de matemáticas, como la duplicación del cubo y números primos. Escribió muchos libros de los cuales sólo se tienen noticias por referencias bibliográficas de otros autores.
Eratóstenes al final de su vida fue afectado por la ceguera y murió de hambre por su propia voluntad en 194 a. C. en Alejandría.
Capitulo II
APORTES
Eratóstenes fue un hombre de ciencia que dedicó su vida a dar respuestas a lo que parecían misterios sin resolver, demostrando con diversos estudios que todo tiene una explicación.
2. - PRINCIPALES APORTES:
Eratóstenes fue el primer científico que se atrevió a demostrar que la tierra no era plana como casi todos pensaban, causando revuelo en su época al explicar científicamente la circunferencia de nuestro planeta. Así tenemos como primer aporte a la humanidad:
2.1. - LA MEDICIÓN DE LAS DIMENSIONES DE LA TIERRA
¿CÓMO MIDIÓ ERATÓSTENES? ¿EN QUÉ SE BASÓ PARA HACER LA MEDIDA DEL RADIO DE LA ESFERA TERRESTRE?
Figura 1
Pues, pensó, sencillamente, que dos estacas clavadas verticalmente en el suelo, a una distancia de varios kilómetros, sobre un mismo meridiano, darían sombras distintas a una misma hora en virtud de la curvatura de la superficie del planeta.
Los ángulos que forman los rayos de sol con la dirección de la estaca son:
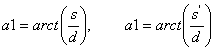
Siendo s y s' la sombra de cada estaca sobre la línea meridiana en cada lugar. La longitud de la estaca es en ambos casos.
Si observamos ahora la figura 2 y nos fijamos en el triángulo que se forma, con ángulos a, a1 y 180-a2, donde a es el ángulo del arco de meridiano comprendido entre las posiciones que ocupan ambas estacas, y a1 y a2 son los ángulos que forman los rayos solares con la dirección de las estacas, vemos que, al sumar 180º los tres ángulos del triángulo es:
a1 + 180 - a2 + a = 180, es decir: a1 - a2 + a = 0, o sea: a = a2 - a1
Figura 2
Conocido el ángulo a, y la longitud L del arco de meridiano entre ambos puntos de colocación de las estacas, será posible, mediante una sencilla regla de tres, encontrar la longitud total, X, de la circunferencia del planeta:
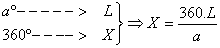
y, de aquí, el radio medio de la Tierra:
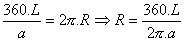
Si una de las dos estacas, en un determinado momento diera sobre la línea meridiana sombra nula, es decir, si en una de las estacas fuera cero el ángulo que forma la dirección de los rayos solares con la estaca, o, dicho de otra manera, si en uno de los dos lugares los rayos solares inciden perpendicularmente, entonces, se tendría que:
a1 = 0, por lo cual a = a2 - 0 = a2, es decir, el ángulo, a, que corresponde al arco de meridiano terrestre comprendido entre ambas posiciones de las estacas, es, precisamente el ángulo, a2, que formarían los rayos solares con la segunda estaca sobre la línea meridiana.
Este último hecho fue lo que utilizó Eratóstenes para hacer su medición.
Eratóstenes, que estaba en Alejandría, recordó que en un cierto día del año, en el solsticio de verano, los rayos solares caían verticalmente en la ciudad de Siena, situada en el mismo meridiano que Alejandría, pues recordaba que el sol se reflejaba en lo mas profundo de los pozos, a la hora del mediodía. Entonces, pensó que si media ese día en la ciudad de Alejandría, a la misma hora, el ángulo, a2, que los rayos solares formaban con la vertical, midiendo la sombra que sobre la línea meridiana formaba la estaca, conocería el ángulo del arco de meridiano entre Alejandría y Siena.
Eratóstenes midió la sombra sobre la línea meridiana producida por una estaca vertical en Alejandría, y conociendo la longitud de la estaca halló ese ángulo a la hora antedicha: resultó que el ángulo era de 7 grados (a2 = 7º). Ya sabia el ángulo del arco de meridiano entre Alejandría y Siena. Ahora faltaba conocer la distancia, a lo largo del meridiano, entre ambas ciudades, es decir, la longitud del arco L. Para ello Eratóstenes pagó a un hombre que hizo, a pié, tal medición. Eran, usando la medida usual en la época y en la zona, unos 4900 estadios, que equivaldría hoy ( a unos 6'125 estadios por kilómetro) a unos 800 kms.
Con estos datos ya es inmediato el cálculo:
Longitud de la circunferencia terrestre:
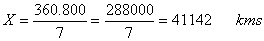
Radio medio del planeta:
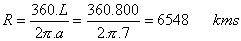
2.2. - MEDICIÓN DEL SOL EN RELACIÓN A LA LUNA
Calculó la distancia del sol en 804.000.000 estadios y la distancia a la luna en 780.000 estadios. Midió casi con precisión la inclinación de la eclíptica en 23 grados 51' 15”.
2.3. - COMPILACIÓN DE ESTRELLAS
Hizo un catálogo de cerca de 675 estrellas y creó uno de los calendarios más avanzados para su época y una historia cronológica del mundo desde la guerra de Troya.
2.4. - SOBRE GEOMETRÍA Y GEOGRAFÍA
Mapa de Eratóstenes (reconstrucción del siglo XIX).
También fue importante su contribución a la geografía, palabra de su invención, que antes de Dicearco, Eudoxio y el propio Eratóstenes, constituía una amalgama de conocimientos dispersos en numerosas obras de viajeros y cronistas. Eratóstenes supo recoger todos estos tesoros que se encontraban en la Biblioteca de Alejandría, conocimientos procedentes en su mayoría de las conquistas de Alejandro Magno, para componer una obra sistemática titulada Geographika, dividida en tres volúmenes: el primero pasaba revista crítica a sus predecesores y exponía las investigaciones acerca de la forma de la Tierra, que él creía una esfera inmóvil; el segundo contenía lo que hoy se llama geografía física, incluyendo el ensayo acerca del tamaño de la Tierra antes comentado; y el último libro versaba sobre geografía política y en el se incluían las descripciones de las comarcas conocidas tomadas de los relatos de viajeros y geógrafos precedentes. Tal como hiciera Dicearco antes, para situar las ciudades tiró una línea paralela al ecuador desde las columnas de Hércules (estrecho de Gibraltar) hasta el extremo oriental de Asia, dividiendo las tierras habitadas en dos partes, y trazó el meridiano por Alejandría y Siena. La obra, según parece, contenía un mapa en el que se indicaban las ciudades y accidentes geográficos, ríos, montañas, lagos, etc. Esta obra no está exenta de polémica ya que Marciano acusó a Eratóstenes de haber plagiado el tratado de Timóstenes Sobre los puertos, lo que desmiente Estrabón cuando afirma que si bien Eratóstenes concedía gran valor a la obra de Timóstenes, en no pocas ocasiones no compartía sus opiniones. Los fragmentos entonces disponibles fueron recopilados y publicados con el título Eratosthenica por Gottfried Bernhardy (Berlín, 1822) junto con otras obras de Eratóstenes.
2.5. - CRIBA DE ERATÒSTENES
La criba de Eratóstenes es un algoritmo que permite hallar todos los números primos menores que un número natural dado N. Se forma una tabla con todos los números naturales comprendidos entre 2 y N y se van tachando los números que no son primos de la siguiente manera: cuando se encuentra un entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos. El proceso termina cuando el cuadrado del mayor numero confirmado como primo es mayor que N.
Determinemos, mediante este procedimiento, la lista de los números primos menores de 20.
Primer paso: Escribamos la lista de los números naturales comprendidos entre 2 y 20.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Segundo paso: Marcamos el primer número no rayado ni marcado como número primo.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Tercer paso: Tachamos todos los múltiplos del número que acabamos de marcar como primo.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Cuarto paso: Si el cuadrado del número recién marcado es inferior a 20, entonces repetimos el segundo paso. Si no, el algoritmo termina, y todos los enteros no tachados son declarados primos.
Como 3² = 9 < 20, volvemos al segundo paso:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
En el cuarto paso, el primer número que no ha sido tachado ni marcado es 5. Como su cuadrado es mayor que 20, el algoritmo termina y consideraremos primos todos los números que no han sido tachados.
RESULTADO: Los números primos comprendidos entre 2 y 20 son: 2, 3, 5, 7, 11, 13, 17, 19.
Conclusiones
Eratóstenes fue un científico matemático que dio grandes aportes a la humanidad:
1.-La medición de la tierra.
2.-La distancia que hay entre el sol y la luna.
3.- La recopilación de estrellas.
4.-A él le debemos que la geografía sea una ciencia donde se estudie la forma de la tierra en cuanto a la longitud, su estado físico y todo lo que en ella hay.
5.-También le debemos el uso de los números primos mediante la criba de Eratóstenes
Bibliografía:
-
Biblioteca de consultas Encarta
ANEXOS
VOCABULARIO MATEMÁTICO
ÀNGULO: Abertura formada por dos rectas que se cortan en un punto llamado vértice.
GEODESIA: Ciencia que trata de determinar la forma o dimensión de la tierra.
LATITUD: La menor de las dos dimensiones principales que tienen las cosas o figuras planas, en contraposición a la longitud.
LOGARITMO: Exponente al que es necesario elevar una cantidad positiva para que resulte un número determinado
LONGITUD: Dimensión mayor de los planos o las cosas.
.SOLSTICIO: Época del año en que el sol está en uno de los dos trópicos.
10
Descargar
| Enviado por: | Leonardo Cueto |
| Idioma: | castellano |
| País: | Perú |
