Equipos electrónicos de consumo
Electrónica digital
Electrónica Digital.
Los sistemas digitales se caracterizan por funcionar en modo binario, es decir, emplean dispositivos mediante sólo son posibles dos estados. Estos dos estados podemos designarlos de varias formas, siendo las más usuales el estado alto y bajo o el 1 lógico y el 0 lógico.
En estos sistemas son el número de impulsos, la duración y la frecuencia de éstos los parámetros a tener en cuenta.
Se establece una división entre sistemas combinacionales y sistemas secuenciales.
Sistemas Combinacionales: El valor de las salidas del sistema depende únicamente del valor de las entradas en ese mismo instante
Sistemas Secuenciales: El valor de las salidas del sistema depende de las entradas en ese mismo instante y en instantes anteriores. Necesitan, pues, algún tipo de memoria para poder almacenar el valor de las entradas en instantes anteriores.
Ejemplos de Sistemas Digitales:
Sistema Morse.
Contador de personas por célula fotoeléctrica.
Sistema de votación.
Sistemas de numeración.
Conjunto de símbolos para representar cantidades. Los más usados en la actualidad son el decimal y el binario. El sistema binario es el usado en circuitos digitales.
Sistema de numeración Binario.
Sólo existen dos símbolos, el 0 y el 1. Una información que sólo puede tomar como valores 0 y 1 se llama BIT, que es la unidad básica de información.
Tomamos como 1 la presencia de señal eléctrica y el 0 como la ausencia de señal eléctrica.
Operaciones Binarias.
Suma binaria.
Para sumar el sistema decimal se hace lo siguiente: se suman las cifras columna a columna, empezando por las unidades. Como el sistema decimal solo permite dígitos del 0 al 9, si el número obtenido es mayor al 9, se le añade un 1 y se resta 10 al resultado. Se repite el proceso hasta sumar todas las columnas yendo de derecha a izquierda.
Resta Binaria.
Cuando, en el sistema decimal, el minuendo es menor al sustraendo, se le suman 10 a la cifra del minuendo y se debe una unidad, que se suma al sustraendo en la siguiente columna.
Multiplicación binaria.
Se multiplica el multiplicador cifra a cifra por el multiplicando. Se repite el multiplicando si el multiplicando es uno, y se pone cero si el multiplicador es cero. Por cada cifra que se multiplica hay que desplazar el resultado a la izquierda un lugar. Se suman los resultados y se obtiene la solución.
División binaria.
Se toman las cifras del dividendo necesarias para que en primera instancia, el dividendo sea mayor que el divisor. A partir de aquí, con los mismos criterios que en la división decimal. Se van bajando cifras una a una. Si el dividendo es mayor que el divisor, el cociente es 1 y, si es menor, el cociente es 0.
Operaciones Lógicas.
No deben confundirse con las aritméticas, las operaciones lógicas son la herramienta de trabajo de los sistemas digitales con la que pueden realizarse las segundas.
Función lógica o Booleana.
Es una combinación de operaciones lógicas aplicadas sobre variables que sólo pueden tomar valores binarios.
Tabla de la verdad.
Representa de forma ordenada todas las posibles combinaciones de valores de entrada y la salida que se obtiene para cada uno de ellos. Para N variables distintas, el número de combinaciones será 2N.
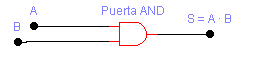
Operación AND.
Operación AND o producto.
S = A · B
Tabla de verdad
| A | B | Salida |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
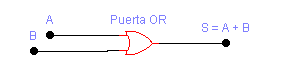
Operación OR.
Operación OR o suma.
S = A + B
Tabla de verdad.
| A | B | Salida |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
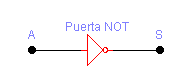
Operación NOT
Operación NOT o inversión.
Opera solamente sobre una variable y el resultado es el valor lógico invertido o complementado.
S = A'
Tabla de Verdad.
| A |
|
| 0 | 1 |
| 1 | 0 |
Operación NAND
Si después de efectuar una operación AND, realizamos una inversión, obtenemos la operación NAND.
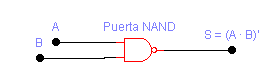
S = (A · B)'
Tabla de verdad.
| A | B | Salida |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Operación NOR.
Si después de efectuar una operación OR, realizamos una inversión, obtendremos la operación NOR.
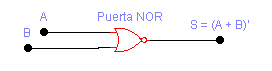
S = (A + B)'
Tabla de verdad.
| A | B | Salida |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
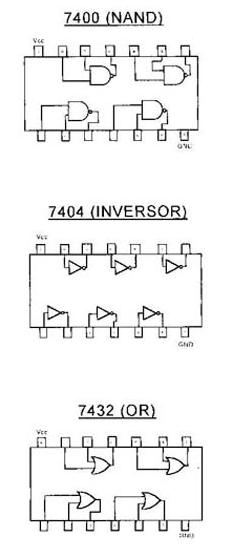
Este tipo de operaciones se realizan mediante circuitos integrados existentes, en los cuales existen puertas de diferentes clases, cada tipo de circuito integrado realiza una operación diferente, nombrándose estos circuitos por números.
Practicas de Digital
1.- Comprobación de puertas.
En esta primera práctica comprobaremos los diferentes tipos de puertas según el siguiente circuito, comprobando su funcionamiento con la tabla de la verdad.
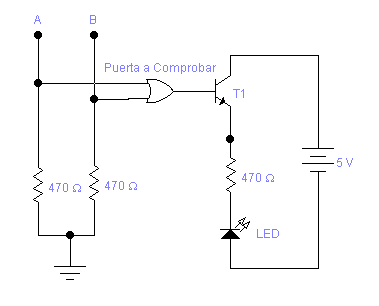
Para hacer A o B 0 ó 1 habrá que suministrarle o dejar de suministrarle +5V, que es la tensión que hemos utilizado para este montaje.
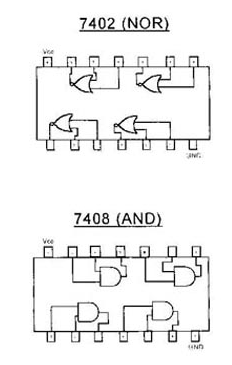
Realizamos este montaje con los integrados 7400 (NAND de 2 entradas), 7404 (Inversor), 7432 (OR de dos entradas), 7402 (NOR de dos entradas), 7408 (AND de dos entradas), obteniendo las siguientes tablas de verdad.
Puertas NAND
| A | B | Salida |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Puertas NOT
| A | S |
| 0 | 1 |
| 1 | 0 |
Puertas OR
| A | B | Salida |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Puertas NOR
| A | B | Salida |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Puertas AND
| A | B | Salida |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2.- Implementación de una función.
Partiendo de una función lógica, debemos hallar su tabla de verdad y montar el circuito lógico correspondiente para demostrar que la tabla de verdad corresponde a la función dada.
Función: S = A'BCD + A'BC'D + (A' + AB)CD + AB
Tabla de verdad
| A | B | C | D | Salida |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
3.- Simplificación Algebraica.
Simplificación algebraica de la función anterior, montando el circuito para comprobar que cumple la misma tabla de verdad.
S = A'BCD + A'BC'D + (A' + AB)CD + ABC'D
= A'BCD + A'BC'D + A'CD + BCD + ABC'D
= A'BD + A'CD + BCD + ABC'D
= D(A'B + A'C + BC + BA)
= D[B(A' + C + A) + A'C]
= D(B + A'C)
= BD + A'CD
4.- Implementación del circuito con puertas NAND
Debemos implementar la función anterior con puertas NAND y comprobar su correcto funcionamiento montando el circuito y comparando las tablas de verdad.
BD + A'CD =
[(BD)'(A'CD)']'
5.- Simplificación de una función por Karnaugh y montaje de ésta para comprobar su resultado con su tabla de verdad.
F="(0,2,3,4,5,6,9,11,12,13,15)
Tabla de verdad
| A | B | C | D | Salida |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Función resultante:
(A'B'C'D')+(A'B'CD')+(A'B'CD)+(A'BC'D')+(A'BC'D)+(A'BCD')+(AB'C'D)+
+(AB'CD)+(ABC'D')+(ABC'D)+(ABCD)
| 00 | 01 | 11 | 10 | |
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | 1 | |
| 11 | 1 | 1 | 1 | |
| 10 | 1 | 1 |
Función simplificada por Karnaugh:
(BC')+(A'C')+(AC'D)+(ACD)+(B'CD)+(A'CD)
6.- Simulación
Dada una situación ficticia dada, debemos de montar un circuito para emular el funcionamiento de dicha situación.
Problema. Necesitamos un sistema que cuando pulsemos un pulsador gire un motor a la derecha, cuando pulsemos otro, gire a la izquierda, si pulsamos otro suene un zumbador, sonando también el zumbador en caso de pulsar simultáneamente los dos pulsadores de giro del motor y que éste no ande.
Para ello necesitaremos tres variables, tantas como pulsadores y tres funciones, tantas como salidas tenemos.
F1 = (AB'C') + (AB'C) AB'
F2 = (A'BC') + (A'BC) A'B
F3 = (A'B'C) + (A'BC) + (AB'C) + (ABC') + (ABC) AB+C
Tabla de verdad.
| A | B | C | S1 | S2 | S3 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
Descargar
| Enviado por: | Wanchu |
| Idioma: | castellano |
| País: | España |