Matemáticas
Ecuaciones diferenciales
Introducción
En el estudio de las ciencias e ingeniería, así como en otros campos tales como, la economía, medicina, psicología, investigación de operaciones entre otros, se desarrollan modelos matemáticos para ayudar a comprender la fenomenología o el origen de ciertos problemas físicos, biológicos, sociales, etc. Estos modelos a menudo dan lugar a una ecuación que contiene ciertas derivadas de una función incógnita o función desconocida. A una ecuación de este tipo se le denomina ecuación diferencial.
Cabe destacar, que la manipulación de una ecuación diferencial no dista mucho del trato dado a una ecuación del tipo algebraico en lo que a la determinación de sus raíces se refiere, de hecho, el objetivo que sigue cada uno de estos dos problemas citados es exactamente el mismo, la determinación de un ente matemático desconocido, llámese función ó llámese variable según sea el caso, que reduzca a la ecuación original a una identidad, dicho en otras palabras, la determinación de una solución que satisfaga a la ecuación dada. Para ilustrar lo anterior analicemos los siguientes ejemplos.
Se desea graficar la función .
Puesto que es una función cuadrática, de los cursos de geometría sabemos que esta, representa una parábola que se puede dibujar del siguiente modo.
Expresemos primero a en una forma más apropiada
por tanto se puede expresar de manera equivalente como
o bien (1)
la expresión anterior nos indica que el vértice de la parábola tiene coordenadas y que abre hacia abajo, sin embargo esta información no es suficiente para hacer el trazo de la gráfica, falta todavía determinar los puntos de intersección de la gráfica de la función y el eje de las s, es decir, los valores de para los cuales .
Si , entonces la función se reduce a la siguiente ecuación algebraica de segundo grado:
siendo en este caso, una incógnita o variable desconocida, la cual pude tomar los valores aun no determinados, tales que
los valores de se pueden obtener resolviendo (2) con la formula general o bien descomponiendo esta en los términos lineales
.
Así concluimos que , son los valores de en donde la gráfica de la función intersecta al eje de las s, y la información necesaria para esbozar la gráfica de esta completa por lo que podemos proceder
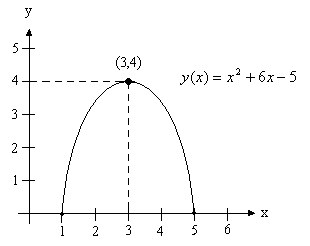
Por otro lado, si reemplazamos los valores en la ecuación (2) tenemos
entonces decimos que por otro lado reducen a la ecuación (2) a una identidad y por tanto concluimos que representan una solución a la ecuación algebraica (2).
Caída Libre de un Cuerpo:
En este ejemplo se puede aplicar la segunda Ley de Newton, la cual establece que la masa del objeto multiplicada por su aceleración es igual a la fuerza total que actúa sobre él. Esto nos conduce a la ecuación diferencial siguiente
Donde “m” es la masa del objeto, la función incógnita o función desconocida “y” es su altura sobre el suelo, “g” la constante de gravedad, y “-mg” la fuerza debida a la gravedad. Cancelando “m” en ambos miembros de (4) esta ecuación diferencial toma la forma:
o equivalentemente
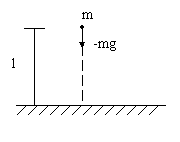
.
En este caso, por integración inmediata es fácil despejar a “y”, en la ecuación anterior, esto es:
por tanto:
,
que representa la velocidad del objeto a cualquier instante de tiempo t.
Repitiendo el mismo proceso en la ecuación anterior se tiene:
así:
Las constantes de integración C1 y C2, se pueden determinar si se conoce su altura y la velocidad inicial del objeto. Así pues, se tiene por un lado, que la función dada en (6) representa una formula para determinar la altura del objeto a cualquier instante de tiempo t, y por otro, una solución a al ecuación diferencial (5), ya que al sustituir (6) y sus derivadas hasta segundo orden en (5), esta última se reduce a una identidad, esto es
por tanto sustituyendo en (5) tenemos la identidad:
Conclusiones
Ejemplo 1:
° La ecuación (2), representa una ecuación algebraica de 2º grado con variable desconocida .
° La ecuación algebraica (2), proporciona información importante acerca de la gráfica de la función, ya que a partir de esta, podemos determinar los puntos de intersección de la gráfica con el eje de las s.
° Los valores , satisfacen a la ecuación algebraica (2) y por tanto son solución única* de la misma.
Ejemplo 2:
° La ecuación (3), representa una ecuación diferencial lineal de 2º orden con función desconocida .
° La ecuación diferencial (3), describe el movimiento de un cuerpo en caída libre, pues a partir de esta, podemos determinar su velocidad y altura a cualquier instante de tiempo t.
° La función obtenida en (6), satisface a la ecuación diferencial (5) y por tanto es solución única** de la misma.
* No existen otros valores de distintos de que satisfagan a la ecuación algebraica (2).
**No existe otra función distinta de (6) que satisfaga a la ecuación diferencial (5). A la función dada en (6) la
llamaremos solución general de la ecuación diferencial dada.
Unidad I
Introducción A Las Ecuaciones Diferenciales
1.1 Definición De Una Ecuación Diferencial
| Definición: | Una ecuación diferencial es una ecuación que involucra las derivadas de una función “desconocida” (o variable dependiente) con respecto de una o más variables (variables independientes). |
1.2 Clasificación De Las Ecuaciones Diferenciales.
Las ecuaciones diferenciales se pueden clasificar de acuerdo con lo siguiente
-
Si la función desconocida depende de una sola variable entonces la ecuación se llama ecuación diferencial ordinaria.
Sin embargo
-
Si la función desconocida depende de más de una variable entonces la ecuación se llama ecuación diferencial parcial.
Ejemplos
| Ecuación | Tipo | Variable Dependiente | Variable Independiente |
| Ordinaria | y | x | |
| Parcial | v | x, y | |
| | Ordinaria | y | x |
| Parcial | u, v | x, y |
Nota: Existen casos particulares en los cuales se tiene más de una variable dependiente, por ejemplo la ecuación siguiente
(Regla de Cauchy)
en la cual tenemos las variables dependientes u y v.
En consecuencia nos veremos forzados a generalizar la definición 1.1 , de la siguiente manera
| Definición: | Una ecuación que contiene las derivadas de una o más variables dependientes, con respecto a una o más variables independientes se llama ecuación diferencial. |
-
Si la ecuación contiene solo derivadas de una o más variables dependientes con respecto a una sola variable independiente, entonces esta se llama ecuación diferencial ordinaria.
-
Si la ecuación diferencial contiene una ó más variables dependientes con respecto a más de una variable independiente esta ecuación se llama ecuación diferencial parcial.
Orden De Una Ecuación Diferencial
| Definición: | El orden de una ecuación diferencial es el indicado por el índice que aparece en la derivada más alta. |
1.3.1 Ejemplos
Ecuación diferencial ordinaria de segundo orden, con variable dependiente y, y variable independiente x.
Ecuación diferencial parcial de tercer orden, con variable dependiente v, y variable independiente x, y.
Grado De Una Ecuación Diferencial
| Definición: | El grado de una ecuación diferencial (que puede escribirse como un polinomio con respecto a las derivadas), es la potencia que aparece en la derivada más alta en la ecuación. |
1.4.1 Ejemplos
| " Es una ecuación diferencial de segundo grado. | |
| " Es una ecuación diferencial de segundo grado. |
Ecuación Diferencial Lineal Ordinaria De Orden n
| Definición: | Una ecuación diferencial ordinaria lineal de orden n, es una ecuación que se puede escribir en la forma ; donde g(x) y los coeficientes , son funciones dadas de x. |
En la ecuación (1), observamos las propiedades características de las ecuaciones diferenciales lineales que se enlistan a continuación:
La variable dependiente “y” y todas sus derivadas son de primer grado, i.e., la potencia de todo término en donde aparece “y” es uno.
Los coeficientes son funciones dadas de la variable independiente x, el coeficiente .
La función g(x) es una función dada de la variable independiente x.
Las funciones de “y” o de las derivadas de “y” tales como , , , , , etc, no pueden aparecer en una ecuación diferencial lineal. Cuando la ecuación diferencial no es lineal, se dice que es no lineal.
1.5.1 Ejemplos
|
| Ecuación diferencial ordinaria, de orden uno, lineal, variable dependiente “y”, variable independiente “x”. |
| Ecuación diferencial ordinaria, de orden dos, lineal, variable dependiente “y” ,variable independiente “x”. | |
| | Ecuación diferencial ordinaria, de orden tres, lineal, variable dependiente “y”, variable independiente “x”. |
| Ecuación diferencial ordinaria, de orden uno, no lineal, variable dependiente “y”, variable independiente “x” | |
| Ecuación diferencial ordinaria, de orden dos, no lineal, variable dependiente “x”, variable independiente “y”. | |
| | Ecuación diferencial ordinaria, de orden cuatro, no lineal, variable dependiente “y” ,variable independiente “x” |
Unificando todos los conceptos vistos al momento, podemos clasificar una ecuación diferencial del siguiente modo
| Ecuación Diferencial | Tipo | Orden | Grado | Linealidad | Variable Dependiente | Variable Independiente |
| Ordinaria | Tres | Uno | Lineal | y | x | |
| Parcial | Dos | Uno | --------- | z | x, y | |
|
| Ordinaria | Tres | Uno | No lineal | y | x |
| Ordinaria | Uno | Uno | Lineal | y | x |
Solución De Una Ecuación Diferencial
| Definición: | Una solución de una ecuación diferencial es cualquier función ó relación que satisface la ecuación, dicho en otras palabras, la reduce a una identidad. |
1.6.1 Soluciones Explícitas
| Definición: | Una función o relación que satisface a una ecuación diferencial y en su estructura la variable dependiente se expresa tan solo en términos de la(s) variable(s) independiente(s) y constante(s) se llama solución explicita. |
1.6.2 Ejemplos
Probar que las funciones definas por
y
son dos soluciones explícitas de la ecuación diferencial
Solución:
Derivando (1)
sustituyendo (1) y sus derivadas en (3)
por tanto
es solución explícita de la ecuación diferencial (3).
Derivando (2)
sustituyendo (2) y sus derivadas en (3)
por tanto
es solución explicita de la ecuación diferencial (3).
Probar que la función definida por
es una solución explícita de
Solución:
Derivando (1)
sustituyendo (1) y sus derivadas en (2)
por tanto,![]()
es solución explícita de la ecuación diferencial.
Probar que la función definida por
es solución explícita de la ecuación diferencial
Solución:
Derivando (1)
sustituyendo (1) y sus derivadas en (2)
por tanto, es solución explicita de la ecuación diferencial
Determine los valores de m tales que
sea una solución de la ecuación diferencial
Solución:
Derivando (1)
sustituyendo (1) y sus derivadas en (2)
o bien
como en (3) , entonces (3) se reducirá a una identidad solo si
resolviendo (4)
por tanto, es solución de (2) si y solo si
.
Comprobación
Si , entonces .
Derivando
sustituyendo y sus derivadas en (2)
por tanto si , entonces es solución de (2).
Si , entonces .
Derivando
sustituyendo y sus derivadas en (2)
por tanto si , entonces es solución de (2).
En todos los ejemplos anteriores hemos tratado soluciones en las cuales la variable dependiente es expresada en función de la(s) variable(s) independiente(s), refiriéndonos a éstas como soluciones explicitas de la ecuación diferencial dada, sin embargo, podemos tener soluciones definidas implícitamente.
1.6.3 Soluciones Implícitas
| Definición: | Una función ó relación que satisface a una ecuación diferencial y que involucra en su estructura tanto variables dependientes como independientes decimos que es una solución implícita de la ecuación diferencial dada. |
1.6.4 Ejemplos
1) La expresión
define a y implícitamente como una función de x. Demostrar que esta función es solución implícita de la ecuación diferencial
Solución:
Derivando implícitamente (1)
derivando nuevamente
sustituyendo (1) y sus derivadas en (2)
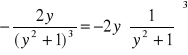
" y3 - 3x + 3y = 5 es solución implícita de (2).
1.7 Problema de Valor Inicial y de Frontera
Analicemos estos dos conceptos mediante el siguiente ejemplo.
Una partícula P se mueve a lo largo del eje x (figura 1.1) de tal menara que su aceleración en cualquier tiempo t " 0 esta dada por .
Encuentre la posición x de la partícula medida del origen O a cualquier tiempo t > 0, asumiendo que inicialmente t = 0 esta localizada en x = 2 y esta viajando a una velocidad v = -5.
Trabaje con la parte a) si solamente se sabe que la partícula esta localizada inicialmente en x = 2 cuando t = 0 y en x = 7 cuando t = 1.
Figura 1.1
x
O P
Sabemos que la aceleración en O de la partícula es
Como v = -5, cuando t = 0, esto es v(0) = -5
así
integrando
Como x = 2, t = 0, esto es x(0) = 2
en consecuencia
de donde (2), define la posición de la partícula en cualquier instante de tiempo t>0.
Considerando nuevamente la aceleración en O de la partícula como
Procediendo como en a) tenemos que la velocidad de la partícula viene dada por
en este caso no existe condición para v(t), entonces integrando nuevamente
determinemos en (4), usando la condición , esto es
así
por otro lado, cuando ; , esto es , entonces de (5)
en consecuencia
de donde (6), define la posición de la partícula en cualquier instante de tiempo del intervalo .
El problema anterior se reduce a resolver las formulaciones matemáticas siguientes
![]()
![]()
Una diferencia importante entre ellas es que en a) las condiciones sobre la función desconocida x y su derivada x' están especificadas en un solo valor de variable independiente (en este caso t = 0). Mientras que en b) las condiciones sobre la función desconocida x se especifican en dos valores (distintos) de la variable independiente (en este caso t = 0 y t = 1).
Los dos tipos de problemas presentados en a) y b) se llaman problemas de valor inicial y de frontera respectivamente.
| Definición: | Un problema de valor inicial, es un problema que busca determinar una solución a una ecuación diferencial sujeta a condiciones sobre la función desconocida y sus derivadas especificadas en un valor de la variable independiente. Tales condiciones se llaman condiciones iniciales. |
| Definición: | Un problema de valor de frontera, es un problema que busca determinar una solución a una ecuación diferencial sujeta a condiciones sobre la función desconocida especificadas en dos o más valores de la variable independiente. Tales condiciones se llaman condiciones de frontera. |
Nota: En general el problema de valor inicial para determinar la solución a una ecuación diferencial de orden n deberá estar sujeto a las condiciones iniciales.
Soluciones Generales y Particulares
Para comprender estos conceptos, resolvamos los siguientes problemas de valor inicial.
Consideremos la ecuación diferencial
sujeta a las siguientes condiciones iniciales
Supongamos que por algún medio la resolvemos y obtenemos que
es solución de la ecuación diferencial (1). Usando en (3) la condición , se tiene
en consecuencia
derivando (4)usando en (4) la condición , se tiene
y por tanto, la solución (3) toma la forma
en el ejemplo
representa la Solución General de la ecuación diferencial (1), mientras que
representa una Solución Particular de (1).
De acuerdo con lo anterior podríamos entonces establecer las siguientes definiciones.
| Definición: | Una función ó relación que satisface a una ecuación diferencial y que involucra en su estructura constantes arbitrarias recibe el nombre de solución general. Así, una ecuación diferencial de orden n tendrá una solución general que involucra n constantes arbitrarias. |
| Definición: | A la solución obtenida de una solución general al seleccionar los valores particulares de las constantes arbitrarias (por ejemplo; para satisfacer condiciones dadas), se le llama solución particular. |
Ejemplos
1) Sea
solución general de
.
a partir de (1) y de la condición inicial obtenga una solución particular para (2).
Solución:
Usando la condición inicial dada en (1)
por tanto la solución particular de (2) es
Comprobación
Derivando (3)
![]()
sustituyendo (3) y su derivada en (1)
2) Sea
solución general de
.
a partir de (1) y de la condición inicial obtenga una solución particular para (2).
Solución:
Usando la condición inicial dada en (1)
por tanto la solución particular implícita de (2) es
Comprobación
Derivando (3)
o bien
sustituyendo (3) y su derivada en (1)
Por otra parte, partiendo de (3) determinemos ahora la forma explícita de la solución particular de (2).
Resolvamos (3) para la variable
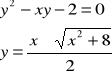
entonces
usando la condición inicial en (4), observamos que se reduce a una identidad, esto es
por tanto
es solución particular explícita de (2), pues satisface la condición inicial dada.
El problema de hallar soluciones generales de ecuaciones diferenciales será tratado más adelante. Un problema más simple es el problema inverso, i-e; hallar la ecuación diferencial a partir del conocimiento de su solución general, esto es, dada la respuesta, encontrar el problema.
Para motivar el procedimiento, consideremos los siguientes ejemplos:
1.8.2 Ejemplos
Encuentre la ecuación diferencial cuya solución general es
Solución:
Derivando (1)
despejando C
sustituyendo (2) en (1)
por tanto
es la ecuación diferencial cuya solución general es (1).
Comprobación
Encuentre la ecuación diferencial cuya solución general es
Solución:
Derivando (1)
sustituyendo (3) en (2)
despejando
sustituyendo(3) y (4) en (1)
por tanto
![]()
es la ecuación diferencial cuya solución general es (1).
1.9 Teorema De Existencia Y Unicidad
Sea dada una ecuación diferencial donde la función está definida en un recinto D del plano XOY que contiene el punto Si la función satisface a las condiciones:
es una función continua de dos variables x e y, en el recinto D;
admite derivada parcial continua con respecto de x e y en el recinto D, entonces, existe una, y sólo una, solución de la ecuación dada que satisface a la condición .
La condición se llama condición inicial.
El problema de la búsqueda de la solución de la ecuación que satisface la condición inicial , lleva el nombre de Cauchy.
Geométricamente esto significa que se busca la curva integral que pasa por el punto dado del plano XOY (fig. 1.2).

Fig. 1.2
El teorema expresa las condiciones suficientes para la existencia de solución única del problema de Cauchy para la ecuación pero estas condiciones no son necesarias. Precisamente, puede existir una solución única de la ecuación que satisface a la condición , a pesar de que en el punto no se cumpla la condición a) o la condición b), o estas condiciones simultáneamente.
1.9.1 Ejemplos
1. Considere la ecuación diferencial
Aquí
En los puntos del eje OX no se cumplen las condiciones a) y b) (la función y su derivada parcial son discontinuas en el eje OX), mas, por cada punto del eje OX pasa por una sola curva integral (fig. 1.3).

Fig. 1.3
2. Considere la ecuación diferencial
El segundo miembro de la ecuación y su derivada parcial son continuas con respecto a x e y en todos los puntos del plano XOY. En virtud del teorema de existencia y unicidad, el recinto en el que la ecuación dada tiene solución única es todo el plano XOY.
3. Considere la ecuación diferencial
El segundo miembro de la ecuación es una función definida y continua en todos los puntos del plano XOY. La derivada parcial se hace infinita para se infringe la condición b) del teorema de existencia y unicidad. Por consiguiente, es posible que no haya unicidad en los puntos del eje OX. Fácilmente se comprueba que la función es solución de la ecuación considerada. Además, la ecuación tiene la solución evidente . Así, pues, por cada punto del eje OX pasan por lo menos dos curvas integrales y, por consiguiente, en los puntos de este eje, verdaderamente, queda infringida la unicidad (fig. 1.4).

Fig. 1.4
Son también líneas integrales las formadas por trozos de las parábolas cúbicas y los segmentos del eje OX; por ejemplo, las líneas ABOC1, ABB2C2, A2B2x, etc. De este modo, por cada punto del eje OX pasan infinitas líneas integrales.
Descargar
| Enviado por: | Ocelot |
| Idioma: | castellano |
| País: | Nicaragua |
