Estadística
Control estadístico de calidad
Manual de SPC (Statistical Process Control)
Índice:
SPC, ¿Qué es?
Herramientas estadísticas
STATISTICAL PROCESS CONTROL
1.- ¿Que es SPC?
SPC (Statistical Process Control) por sus cifras en ingles, es la aplicación de métodos estadísticos para identificar y controlar la causa de una variación dentro de un proceso.
El SPC es el equivalente a un histograma visto desde el punto de vista del tiempo. Cada punto nuevo es estadísticamente comparado con los puntos anteriores así como con la distribución como un todo en función de encontrar consideraciones en el control de proceso (control i.e., turnos y modas).
Formas con zonas y reglas son creadas y usadas para simplificar el monitoreo y la toma de decisiones al nivel del operador. SPC separa variación de la causa especial de la causa común en un proceso al nivel de confidencia creado en las reglas a seguir (usualmente 99.73% o 3 Sigma).
El Control Estadístico de Procesos es un conjunto de herramientas estadísticas que permiten recopilar, estudiar y analizar la información de procesos repetitivos para poder tomar decisiones encaminadas a la mejora de los mismos, es aplicable tanto a procesos productivos como de servicios siempre y cuando cumplan con dos condiciones: Que se mensurable (observable) y que sea repetitivo. El propósito fundamental de CEP es identificar y eliminar las causas especiales de los problemas (variación) para llevar a los procesos nuevamente bajo control.
El CEP sirve para llevar a la empresa del Control de Calidad "Correctivo" por inspección, de pendiente de una sola área, al Control de Calidad "Preventivo" por producción, dependiente de las áreas productivas, y posteriormente al Control de Calidad "Predictivo" por diseño, dependiendo de todas las áreas de la empresa. En la figura 1 se muestra el ciclo de aplicación del Control Estadístico de Proceso
Todo proceso productivo es un sistema formado por personas, equipos y procedimientos de trabajo. El proceso genera una salida (output), que es el producto que se quiere fabricar. La calidad del producto fabricado está determinada por sus características de calidad, es decir, por sus propiedades físicas, químicas, mecánicas, estéticas, durabilidad, funcionamiento, etc. que en conjunto determinan el aspecto y el comportamiento del mismo. El cliente quedará satisfecho con el producto si esas características se ajustan a lo que esperaba, es decir, a sus expectativas previas.
Por lo general, existen algunas características que son críticas para establecer la calidad del producto. Normalmente se realizan mediciones de estas características y se obtienen datos numéricos. Si se mide cualquier característica de calidad de un producto, se observará que los valores numéricos presentan una fluctuación o variabilidad entre las distintas unidades del producto fabricado.
2.- Herramientas estadísticas
Diagrama de causa-efecto. Hemos visto en la introducción como el valor de una característica de calidad depende de una combinación de variables y factores que condicionan el proceso productivo. Vamos a continuar con el ejemplo de fabricación de mayonesa para explicar los Diagramas de Causa-Efecto:
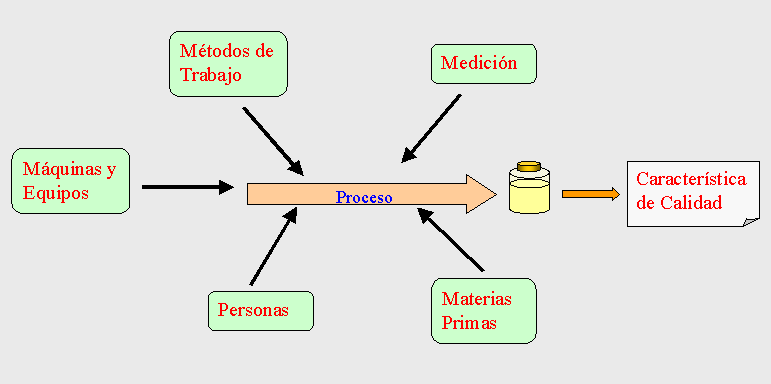
La variabilidad de las características de calidad es un efecto observado que tiene múltiples causas. Cuando ocurre algún problema con la calidad del producto, debemos investigar para identificar las causas del mismo. Para ello nos sirven los Diagramas de Causa - Efecto, conocidos también como Diagramas de Espina de Pescado por la forma que tienen. Estos diagramas fueron utilizados por primera vez por Kaoru Ishikawa.
Para hacer un Diagrama de Causa-Efecto seguimos estos pasos:
Decidimos cual va a ser la característica de calidad que vamos a analizar. Por ejemplo, en el caso de la mayonesa podría ser el peso del frasco lleno, la densidad del producto, el porcentaje de aceite, etc.
Trazamos un flecha gruesa que representa el proceso y a la derecha escribimos la característica de calidad:
Indicamos los factores causales más importantes y generales que puedan generar la fluctuación de la característica de calidad, trazando flechas secundarias hacia la principal. Por ejemplo, Materias Primas, Equipos, Operarios, Método de Medición, etc.:
Incorporamos en cada rama factores más detallados que se puedan considerar causas de fluctuación. Para hacer esto, podemos formularnos estas preguntas:
a) ¿Por qué hay fluctuación o dispersión en los valores de la característica de calidad? Por la fluctuación de las Materias Primas. Se anota Materias Primas como una de las ramas principales.
b) ¿Qué Materias Primas producen fluctuación o dispersión en los valores de la característica de calidad? Aceite, Huevos, sal, otros condimentos. Se agrega Aceite como rama menor de la rama principal Materias Primas.
c) ¿Por qué hay fluctuación o dispersión en el aceite? Por la fluctuación de la cantidad agregada a la mezcla. Agregamos a Aceite la rama más pequeña Cantidad.
d) ¿Por qué hay variación en la cantidad agregada de aceite? Por funcionamiento irregular de la balanza. Se registra la rama Balanza.
e) ¿Por qué la balanza funciona en forma irregular? Por que necesita mantenimiento. En la rama Balanza colocamos la rama Mantenimiento.
Así seguimos ampliando el Diagrama de Causa-Efecto hasta que contenga todas las causas posibles de dispersión.
Finalmente verificamos que todos los factores que puedan causar dispersión hayan sido incorporados al diagrama. Las relaciones Causa-Efecto deben quedar claramente establecidas y en ese caso, el diagrama está terminado.
Planillas de dispersión.- Los datos que se obtienen al medir una característica de calidad pueden recolectarse utilizando Planillas de Inspección. Las Planillas de Inspección sirven para anotar los resultados a medida que se obtienen y al mismo tiempo observar cual es la tendencia central y la dispersión de los mismos. Es decir, no es necesario esperar a recoger todos los datos para disponer de información estadística.
¿Cómo realizamos las anotaciones? En lugar de anotar los números, hacemos una marca de algún tipo (*, +, raya, etc.) en la columna correspondiente al resultado que obtuvimos.
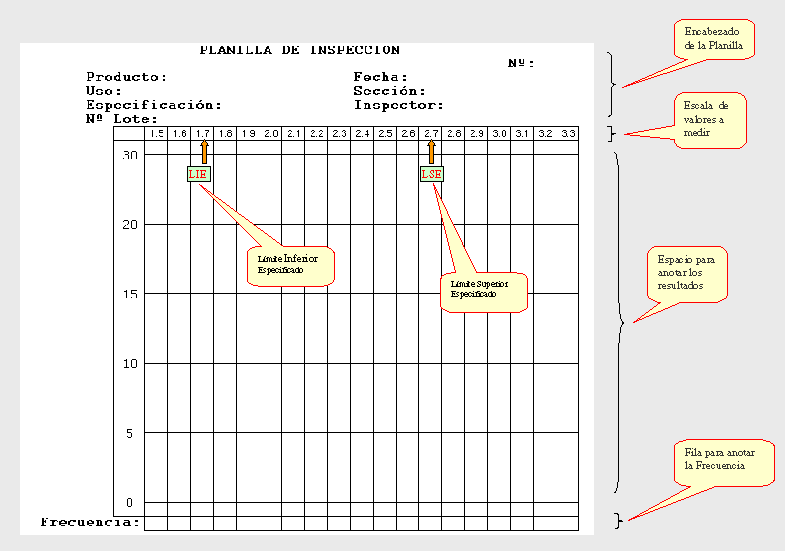
Vamos a suponer que tenemos un lote de artículos y realizamos algún tipo de medición. En primer lugar, registramos en el encabezado de la planilla la información general: Nº de Planilla, Nombre del Producto, Fecha, Nombre del Inspector, Nº de Lote, etc. Esto es muy importante porque permitirá identificar nuestro trabajo de medición en el futuro.
Luego realizamos las mediciones y las vamos anotando en la Planilla. Por ejemplo, si obtuvimos los tres valores siguientes 1.8, 2.6, 2.6 y los registramos con un signo + quedaría así:
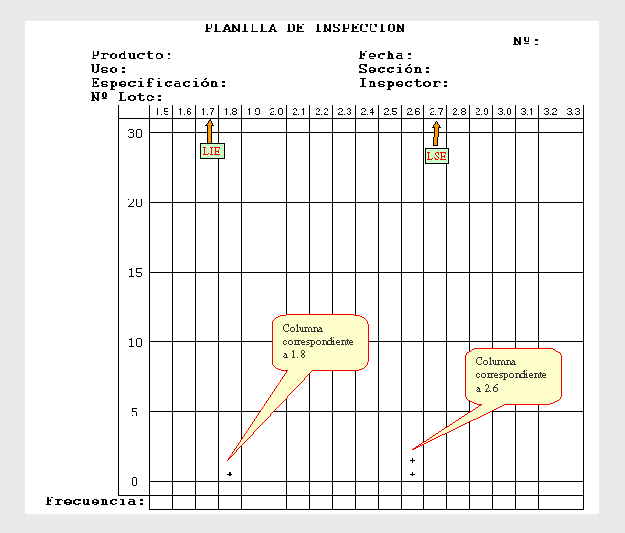
Después de muchas mediciones, nuestra planilla quedaría como sigue:
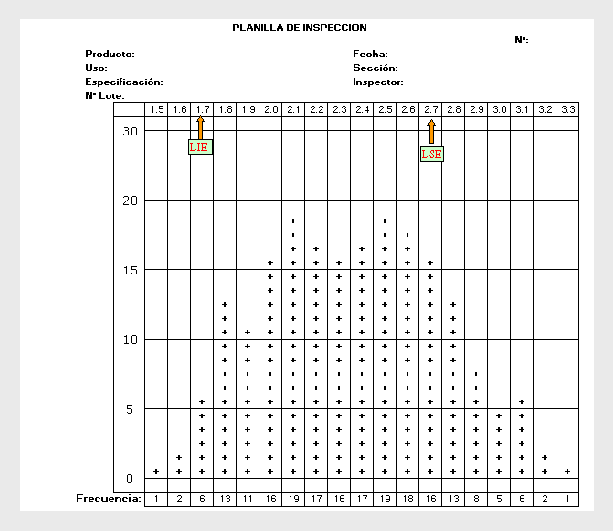
Para cada columna contamos el total de resultados obtenidos y lo anotamos al pié. Esta es la Frecuencia de cada resultado, que nos dice cuáles mediciones se repitieron más veces.
¿Qué información nos brinda la Planilla de Inspección? Al mismo tiempo que medimos y registramos los resultados, nos va mostrando cual es la Tendencia Central de las mediciones. En nuestro caso, vemos que las mismas están agrupadas alrededor de 2.3 aproximadamente, con un pico en 2.1 y otro en 2.5 . Habría que investigar por que la distribución de los datos tiene esa forma. Además podemos ver la Dispersión de los datos. En este caso vemos que los datos están dentro de un rango que comienza en 1.5 y termina en 3.3 . Nos muestra entonces una información acerca de nuestros datos que no sería fácil de ver si sólo tuviéramos una larga lista con los resultados
Gráficos de control.- Un gráfico de control es una carta o diagrama especialmente preparado donde se van anotando los valores sucesivos de la característica de calidad que se está controlando. Los datos se registran durante el funcionamiento del proceso de fabricación y a medida que se obtienen.
El gráfico de control tiene una Línea Central que representa el promedio histórico de la característica que se está controlando y Límites Superior e Inferior que también se calculan con datos históricos.
Por ejemplo, supongamos que se tiene un proceso de fabricación de anillos de pistón para motor de automóvil y a la salida del proceso se toman las piezas y se mide el diámetro. Las mediciones sucesivas del diámetro de los anillos se pueden anotar en una carta como la siguiente:
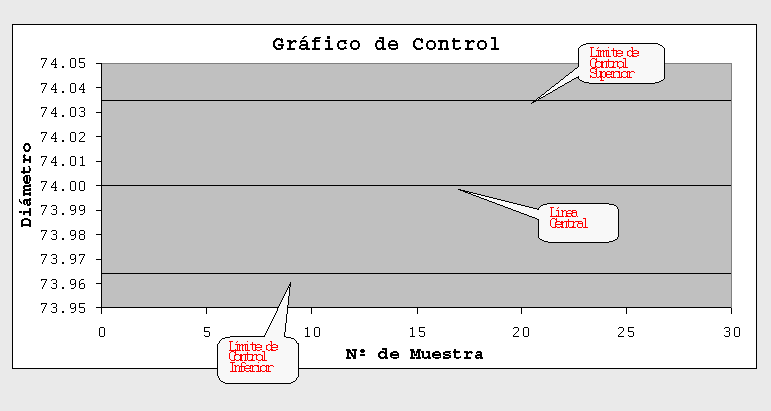
Por ejemplo, si las 15 últimas mediciones fueron las siguientes:
Entonces tendríamos un Gráfico de Control como este:
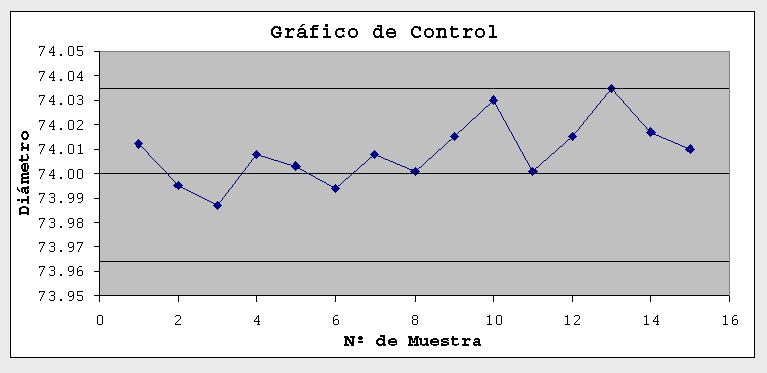
Podemos observar en este gráfico que los valores fluctúan al azar alrededor del valor central (Promedio histórico) y dentro de los límites de control superior e inferior. A medida que se fabrican, se toman muestras de los anillos, se mide el diámetro y el resultado se anota en el gráfico, por ejemplo, cada media hora.
Pero ¿Qué ocurre cuando un punto se va fuera de los límites? Eso es lo que ocurre con el último valor en el siguiente gráfico:
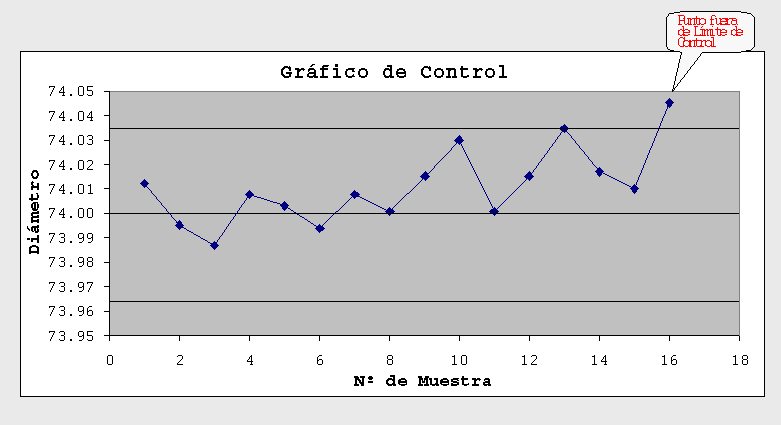
Esa circunstancia puede ser un indicio de que algo anda mal en el proceso. Entonces, es necesario investigar para encontrar el problema (Causa Asignable) y corregirla. Si no se hace esto el proceso estará funcionando a un nivel de calidad menor que originalmente.
Existen diferentes tipos de Gráficos de Control: Gráficos X-R, Gráficos C, Gráficos np, Gráficos Cusum, y otros. Cuando se mide una característica de calidad que es una variable continua se utilizan en general los Gráficos X-R. Estos en realidad son dos gráficos que se utilizan juntos, el de X (promedio del subgrupo) y el de R (rango del subgrupo). En este caso se toman muestras de varias piezas, por ejemplo 5 y esto es un subgrupo. En cada subgrupo se calcula el promedio X y el rango R (Diferencia entre el máximo y el mínimo).
A continuación podemos observar un típico gráfico de X:
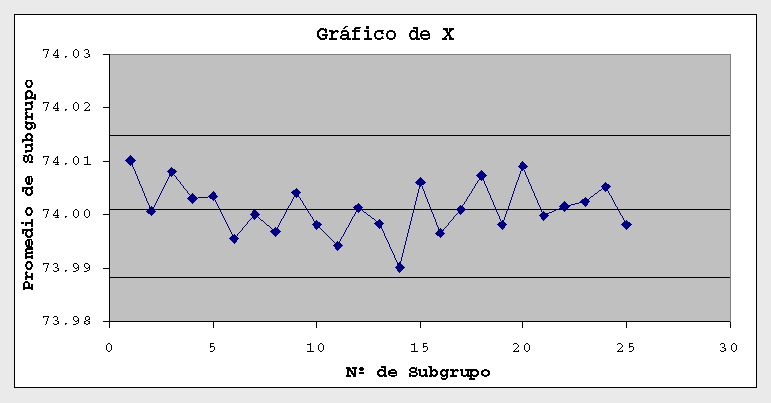
Y lo que sigue es un gráfico de R:
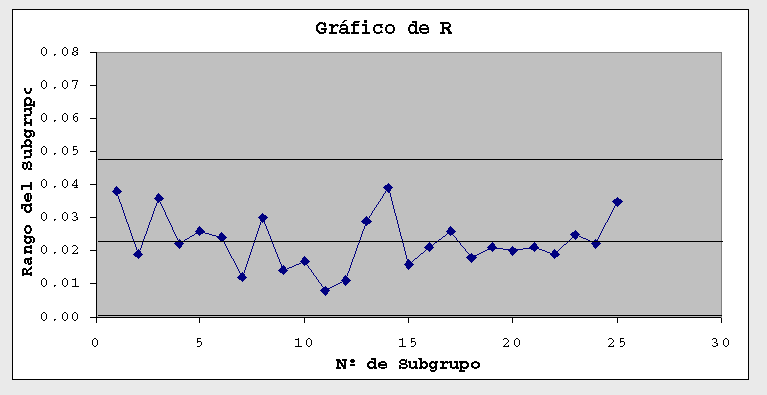
El gráfico de X permite controlar la variabilidad entre los sucesivos subgrupos y el de R permite controlar la variabilidad dentro de cada subgrupo
Diagrama de flujo.- Diagrama de Flujo es una representación gráfica de la secuencia de etapas, operaciones, movimientos, decisiones y otros eventos que ocurren en un proceso. Esta representación se efectúa a través de formas y símbolos gráficos utilizados usualmente:
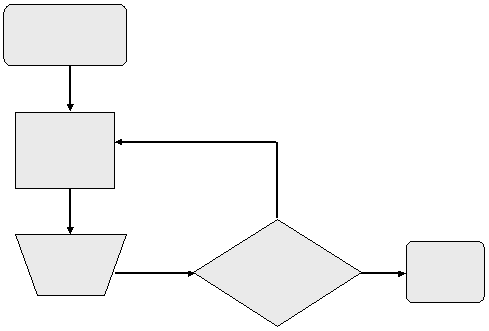
Los símbolos gráficos para dibujar un diagrama de flujo están más o menos normalizados: 

Existen otros símbolos que se pueden utilizar. Lo importante es que su significado se entienda claramente a primera vista. En el ejemplo siguiente, vemos un diagrama de flujo para representar el proceso de fabricación de una resina (Reacción de Polimerización):

Histogramas.- Un histograma es un gráfico o diagrama que muestra el número de veces que se repiten cada uno de los resultados cuando se realizan mediciones sucesivas. Esto permite ver alrededor de que valor se agrupan las mediciones (Tendencia central) y cual es la dispersión alrededor de ese valor central.
Supongamos que un médico dietista desea estudiar el peso de personas adultas de sexo masculino y recopila una gran cantidad de datos midiendo el peso en kilogramos de sus pacientes varones:
| 74.6 | 74.6 | 81.6 | 75.4 | 69.8 | 68.4 |
| 74.5 | 85.9 | 65.8 | 63.5 | 95.7 | 69.4 |
| 77.0 | 113.7 | 57.8 | 69.9 | 74.5 | 74.3 |
| 70.7 | 77.9 | 74.5 | 63.7 | 77.0 | 63.2 |
| 79.4 | 76.4 | 77.0 | 72.1 | 70.7 | 68.4 |
| 74.6 | 95.7 | 70.7 | 71.6 | 79.4 | 76.9 |
| 85.2 | 78.4 | 79.4 | 69.4 | 74.6 | 75.4 |
| 81.6 | 84.6 | 74.6 | 69.8 | 85.2 | 74.8 |
| 67.9 | 97.4 | 85.2 | 83.5 | 81.6 | 78.9 |
| 63.7 | 74.5 | 81.6 | 69.7 | 67.9 | 77.0 |
| 72.1 | 77.0 | 67.9 | 68.4 | 63.7 | 76.7 |
| 71.6 | 70.7 | 63.7 | 70.7 | 72.1 | 77.0 |
| 69.4 | 79.4 | 72.1 | 79.4 | 71.6 | 70.7 |
| 69.8 | 74.6 | 71.6 | 74.6 | 69.4 | 79.4 |
| 83.5 | 85.2 | 69.4 | 85.2 | 69.8 | 74.6 |
| 83.5 | 81.6 | 69.8 | 81.6 | 83.5 | 85.2 |
| 74.9 | 67.9 | 83.5 | 67.9 | 79.3 | 81.6 |
| 73.2 | 63.7 | 74.9 | 63.7 | 76.3 | 67.9 |
| 70.7 | 70.7 | 73.2 | 67.5 | 79.8 | 63.7 |
| 79.4 | 79.4 | 70.7 | 85.3 | 70.7 | 72.1 |
| 88.6 | 74.6 | 79.4 | 88.6 | 79.4 | 71.6 |
| 70.7 | 85.2 | 74.6 | 70.7 | 74.6 | 69.4 |
| 79.4 | 81.6 | 85.2 | 79.4 | 85.2 | 69.8 |
| 70.7 | 67.9 | 81.6 | 74.6 | 81.6 | 83.5 |
| 79.4 | 63.7 | 67.9 | 85.2 | 67.9 | 67.9 |
| 74.6 | 72.1 | 63.7 | 81.6 | 63.7 | 63.7 |
| 85.2 | 71.6 | 72.1 | 67.9 | 72.1 | 70.7 |
| 81.6 | 69.4 | 71.6 | 63.7 | 71.6 | 73.2 |
| 67.9 | 69.8 | 69.4 | 72.1 | 69.4 | 70.7 |
| 63.7 | 83.5 | 69.8 | 71.6 | 69.8 | 79.4 |
| 72.1 | 83.5 | 83.5 | 69.4 | 83.5 | 74.6 |
| 71.6 | 69.7 | 85.2 | 69.8 | 69.8 | 63.7 |
| 69.4 | 68.4 | 81.6 | 83.5 | 83.5 | 72.1 |
| 69.8 | 70.7 | 63.7 | 72.1 | 83.5 | 71.6 |
| 83.5 | 79.4 | 72.1 | 71.6 | 72.1 | 69.4 |
| 67.9 | 71.6 | 71.6 | 69.4 | 71.6 | 69.8 |
Así como están los datos es muy difícil sacar conclusiones acerca de ellos.
Entonces, lo primero que hace el médico es agrupar los datos en intervalos contando cuantos resultados de mediciones de peso hay dentro de cada intervalo (Esta es la frecuencia). Por ejemplo, ¿Cuántos pacientes pesan entre 60 y 65 kilos? ¿Cuántos pacientes pesan entre 65 y 70 kilos?:
| Intervalos | Nº Pacientes (Frecuencia) |
| <50 | 0 |
| 50-55 | 0 |
| 55-60 | 1 |
| 60-65 | 17 |
| 65-70 | 48 |
| 70-75 | 70 |
| 75-80 | 32 |
| 80-85 | 28 |
| 85-90 | 16 |
| 90-95 | 0 |
| 95-100 | 3 |
| 100-105 | 0 |
| 105-110 | 0 |
| >110 | 1 |
Ahora se pueden representar las frecuencias en un gráfico como el siguiente:

Por ejemplo, la tabla nos dice que hay 48 pacientes que pesan entre 65 y 70 kilogramos. Por lo tanto, levantamos una columna de altura proporcional a 48 en el gráfico:

Y agregando el resto de las frecuencias nos queda el histograma siguiente:

¿Qué utilidad nos presta el histograma? Permite visualizar rápidamente información que estaba oculta en la tabla original de datos. Por ejemplo, nos permite apreciar que el peso de los pacientes se agrupa alrededor de los 70-75 kilos. Esta es la Tendencia Central de las mediciones. Además podemos observar que los pesos de todos los pacientes están en un rango desde 55 a 100 kilogramos. Esta es la Dispersión de las mediciones. También podemos observar que hay muy pocos pacientes por encima de 90 kilogramos o por debajo de 60 kilogramos.
Ahora el médico puede extraer toda la información relevante de las mediciones que realizó y puede utilizarlas para su trabajo en el terreno de la medicina.
El Diagrama de Pareto.- es un histograma especial, en el cual las frecuencias de ciertos eventos aparecen ordenadas de mayor a menor. Vamos a explicarlo con un ejemplo.
Supongamos que un fabricante de heladeras desea analizar cuales son los defectos más frecuentes que aparecen en las unidades al salir de la línea de producción. Para esto, empezó por clasificar todos los defectos posibles en sus diversos tipos:
| Tipo de Defecto | Detalle del Problema |
| Motor no detiene | No para el motor cuando alcanza Temperatura |
| No enfría | El motor arranca pero la heladera no enfría |
| Burlete Def. | Burlete roto o deforme que no ajusta |
| Pintura Def. | Defectos de pintura en superficies externas |
| Rayas | Rayas en las superficies externas |
| No funciona | Al enchufar no arranca el motor |
| Puerta no cierra | La puerta no cierra correctamente |
| Gavetas Def. | Gavetas interiores con rajaduras |
| Motor no arranca | El motor no arranca después de ciclo de parada |
| Mala Nivelación | La heladera se balancea y no se puede nivelar |
| Puerta Def. | Puerta de refrigerador no cierra herméticamente |
| Otros | Otros Defectos no incluidos en los anteriores |
Posteriormente, un inspector revisa cada heladera a medida que sale de producción registrando sus defectos de acuerdo con dichos tipos.
Después de inspeccionar 88 heladeras, se obtuvo una tabla como esta:
| Tipo de Defecto | Detalle del Problema | Nº |
| Burlete Def. | Burlete roto o deforme que no ajusta | 9 |
| Pintura Def. | Defectos de pintura en superficies externas | 5 |
| Gavetas Def. | Gavetas interiores con rajaduras | 1 |
| Mala Nivelación | La heladera se balancea y no se puede nivelar | 1 |
| Motor no arranca | El motor no arranca después de ciclo de parada | 1 |
| Motor no detiene | No para el motor cuando alcanza Temperatura | 36 |
| No enfría | El motor arranca pero la heladera no enfría | 27 |
| No funciona | Al enchufar no arranca el motor | 2 |
| Otros | Otros Defectos no incluidos en los anteriores | 0 |
| Puerta Def. | Puerta de refrigerador no cierra herméticamente | 0 |
| Puerta no cierra | La puerta no cierra correctamente | 2 |
| Rayas | Rayas en las superficies externas | 4 |
| Total: | 88 |
La última columna muestra el número de heladeras que presentaban cada tipo de defecto, es decir, la frecuencia con que se presenta cada defecto. En lugar de la frecuencia numérica podemos utilizar la frecuencia porcentual, es decir, el porcentaje de heladeras en cada tipo de defecto:
| Tipo de Defecto | Detalle del Problema | Frec. | Frec. % |
| Burlete Def. | Burlete roto o deforme que no ajusta | 9 | 10.2 |
| Pintura Def. | Defectos de pintura en superficies externas | 5 | 5.7 |
| Gavetas Def. | Gavetas interiores con rajaduras | 1 | 1.1 |
| Mala Nivelación | La heladera se balancea y no se puede nivelar | 1 | 1.1 |
| Motor no arranca | El motor no arranca después de ciclo de parada | 1 | 1.1 |
| Motor no detiene | No para el motor cuando alcanza Temperatura | 36 | 40.9 |
| No enfría | El motor arranca pero la heladera no enfría | 27 | 30.7 |
| No funciona | Al enchufar no arranca el motor | 2 | 2.3 |
| Otros | Otros Defectos no incluidos en los anteriores | 0 | 0.0 |
| Puerta Def. | Puerta de refrigerador no cierra herméticamente | 0 | 0.0 |
| Puerta no cierra | La puerta no cierra correctamente | 2 | 2.3 |
| Rayas | Rayas en las superficies externas | 4 | 4.5 |
| Total: | 88 | 100 |
Podemos ahora representar los datos en un histograma como el siguiente:

A continuación, en cada intervalo dibujamos una columna de altura proporcional al porcentaje de heladeras que presenta ese tipo de defecto (Ultima columna de la tabla):

Pero ¿Cuáles son los defectos que aparecen con mayor frecuencia? Para hacerlo más evidente, antes de graficar podemos ordenar los datos de la tabla en orden decreciente de frecuencia:
| Tipo de Defecto | Detalle del Problema | Frec. | Frec. % |
| Motor no detiene | No para el motor cuando alcanza Temperatura | 36 | 40.9 |
| No enfría | El motor arranca pero la heladera no enfría | 27 | 30.7 |
| Burlete Def. | Burlete roto o deforme que no ajusta | 9 | 10.2 |
| Pintura Def. | Defectos de pintura en superficies externas | 5 | 5.7 |
| Rayas | Rayas en las superficies externas | 4 | 4.5 |
| No funciona | Al enchufar no arranca el motor | 2 | 2.3 |
| Puerta no cierra | La puerta no cierra correctamente | 2 | 2.3 |
| Gavetas Def. | Gavetas interiores con rajaduras | 1 | 1.1 |
| Mala Nivelación | La heladera se balancea y no se puede nivelar | 1 | 1.1 |
| Motor no arranca | El motor no arranca después de ciclo de parada | 1 | 1.1 |
| Otros | Otros Defectos no incluidos en los anteriores | 0 | 0.0 |
| Puerta Def. | Puerta de refrigerador no cierra herméticamente | 0 | 0.0 |
| Total: | 88 | 100 |
Lo que obtenemos se llama Diagrama de Pareto o Gráfico de Pareto:

Ahora resulta evidente cuales son los tipos de defectos más frecuentes. Podemos observar que los 3 primeros tipos de defectos se presentan en el 82 % de las heladeras, aproximadamente. Esto nos conduce a lo que se conoce como Principio de Pareto: La mayor parte de los defectos encontrados en el lote pertenece sólo a 2 ó 3 tipos de defectos, de manera que si se eliminan las causas que los provocan desaparecería la mayor parte de los defectos.
Gráficos de control.- Los Diagramas de Dispersión o Gráficos de Correlación permiten estudiar la relación entre 2 variables. Dadas 2 variables X e Y, se dice que existe una correlación entre ambas si cada vez que aumenta el valor de X aumenta proporcionalmente el valor de Y (Correlación positiva) o si cada vez que aumenta el valor de X disminuye en igual proporción el valor de Y (Correlación negativa).
En un gráfico de correlación representamos cada par X, Y como un punto donde se cortan las coordenadas de X e Y:

Veamos un ejemplo. Supongamos que tenemos un grupo de personas adultas de sexo masculino. Para cada persona se mide la altura en metros (Variable X) y el peso en kilogramos (Variable Y). Es decir, para cada persona tendremos un par de valores X, Y que son la altura y el peso de dicha persona:
| Nº Persona | Altura (m) | Peso (Kg.) | Nº Persona | Altura (m) | Peso (Kg.) |
| 001 | 1.94 | 95.8 | 026 | 1.66 | 74.9 |
| 002 | 1.82 | 80.5 | 027 | 1.96 | 88.1 |
| 003 | 1.79 | 78.2 | 028 | 1.56 | 65.3 |
| 004 | 1.69 | 77.4 | 029 | 1.55 | 64.5 |
| 005 | 1.80 | 82.6 | 030 | 1.71 | 75.5 |
| 006 | 1.88 | 87.8 | 031 | 1.90 | 91.3 |
| 007 | 1.57 | 67.6 | 032 | 1.65 | 66.6 |
| 008 | 1.81 | 82.5 | 033 | 1.78 | 76.8 |
| 009 | 1.76 | 82.5 | 034 | 1.83 | 80.2 |
| 010 | 1.63 | 65.8 | 035 | 1.98 | 97.6 |
| 011 | 1.59 | 67.3 | 036 | 1.67 | 76.0 |
| 012 | 1.84 | 88.8 | 037 | 1.53 | 58.0 |
| 013 | 1.92 | 93.7 | 038 | 1.96 | 95.2 |
| 014 | 1.84 | 82.9 | 039 | 1.66 | 74.5 |
| 015 | 1.88 | 88.4 | 040 | 1.62 | 71.8 |
| 016 | 1.62 | 69.0 | 041 | 1.89 | 91.0 |
| 017 | 1.86 | 83.4 | 042 | 1.53 | 62.1 |
| 018 | 1.91 | 89.1 | 043 | 1.59 | 69.8 |
| 019 | 1.99 | 95.2 | 044 | 1.55 | 64.6 |
| 020 | 1.76 | 79.1 | 045 | 1.97 | 90.0 |
| 021 | 1.55 | 61.6 | 046 | 1.51 | 63.8 |
| 022 | 1.71 | 70.6 | 047 | 1.59 | 62.6 |
| 023 | 1.75 | 79.4 | 048 | 1.60 | 67.8 |
| 024 | 1.76 | 78.1 | 049 | 1.57 | 63.3 |
| 025 | 2.00 | 90.6 | 050 | 1.61 | 65.2 |
Entonces, para cada persona representamos su altura y su peso con un punto en un gráfico:

Una vez que representamos a las 50 personas quedará un gráfico como el siguiente:

¿Qué nos muestra este gráfico? En primer lugar podemos observar que las personas de mayor altura tienen mayor peso, es decir parece haber una correlación positiva entre altura y peso. Pero un hombre bajito y gordo puede pesar más que otro alto y flaco. Esto es así porque no hay una correlación total y absoluta entre las variables altura y peso. Para cada altura hay personas de distinto peso:

Sin embargo podemos afirmar que existe cierto grado de correlación entre la altura y el peso de las personas.
Cuando se trata de dos variables cualesquiera, puede no haber ninguna correlación o puede existir alguna correlación en mayor o menor grado, como podemos ver en los gráficos siguientes: 




Por ejemplo, en el siguiente gráfico podemos ver la relación entre el contenido de Humedad de hilos de algodón y su estiramiento:


Descargar
| Enviado por: | Ernesto Muñoz |
| Idioma: | castellano |
| País: | México |
