Electrónica, Electricidad y Sonido
Contadores
Índice.
Introducción.
En la actualidad, los sistemas digitales son muy utilizados y variados para diferentes tipos de aplicaciones las cuales en su mayoría son aplicadas en la industria y en mayor parte de los equipos electrónicos.
Es por esto que es necesario saber a grandes rasgos las aplicaciones, y como funcionan los diferentes tipos de sistemas digitales, así nosotros poder desarrollar la capacidad de aplicar y de poder trabajar con ellos sin ningún tipo de dificultad.
Es por esto que a continuación le presentamos el siguiente trabajo, destinado a comprender de mejor manera las distintas funciones y aplicaciones de los contadores.
1. Contadores asíncronos de rizos.
Este tipo de contadores donde cada salida del flip-flop sirve como señal de entrada CLK para el siguiente flip-flop, estos contadores no cambian de estado todos juntos por lo que se dice que no están en sincronía, solo el primer flip flop responde a los pulsos del reloj ,luego para que al segundo flip-flop responda debe esperar que el primer flip-flop cambie de estado, y para que el tercer flip-flop se complemente debe esperar que el segundo flip-flop cambie de estado, y así sucesivamente con los demás flip-flop. Por lo tanto existe un leve retraso entre las respuestas de cada flip-flop, en los ff modernos este retraso es relativamente corto va del orden de los 10-40nsg.
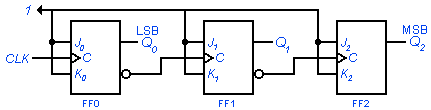
. En el diagrama lógico se muestra un contador asíncrono binario ascendente de tres bits diseñado a partir de flip-flop J-K en configuración toggle con disparo por borde de subida. Debido a que posee tres flip-flop, su ciclo básico se compone de ocho estados que van desde cero (000) hasta siete (111) en forma secuencial y repetitiva.
También podemos observar la tabla de verdad del circuito donde Q2 es el termino más significativo.
| Q2 | Q1 | Q0 | N° de pulsos del reloj |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 2 |
| 0 | 1 | 1 | 3 |
| 1 | 0 | 0 | 4 |
| 1 | 0 | 1 | 5 |
| 1 | 1 | 0 | 6 |
| 1 | 1 | 1 | 7 |
Asumiendo el estado inicial de la salida en 000, al llegar el primer pulso de reloj Q0 cambia de estado dicho cambio es detectado por el siguiente flip-flop (J2-K2) el cual considera que este cambio como su señal de reloj que lo hace cambiar de estado.
.
. En el diagrama lógico se muestra un contador asíncrono binario ascendente de tres bits diseñado a partir de flip-flop J-K en configuración toggle con disparo por borde de subida. Debido a que posee tres flip-flops, su ciclo básico se compone de ocho estados que van desde cero (000) hasta siete (111) en forma secuencial y repetitiva.
Asumiendo el estado inicial de la salida en 000, al llegar el primer pulso de reloj Q0 cambia de estado dicho cambio es detectado por el siguiente flip-flop (J2-K2) el cual considera que este cambio como su señal de reloj que lo hace cambiar de estado.
2. Numero MOD.
El contador de la figura anterior, tiene 8 estados diferentes del 000 al 111 por tanto se trata de un contador de rizos MOD 8, recordamos que el numero MOD siempre es igual al numero de estados por los cuales pasa el contador en cada ciclo completo antes que se recicle hacia su estado inicial.
El numero MOD lo podemos aumentar, simplemente aumentando el numero de flip-flop al contador. Es decir el numero MOD es igual a 2N donde N es el numero de flip-flop conectados en la configuración anterior.
3. División de frecuencia.
En la figura podemos ver que en el contador básico cada flip-flop da una forma de onda de salida que es exactamente la mitad de la frecuencia de la onda de su entrada CLK. Supongamos que los pulsos de la señal del reloj es de 8Hz, así podemos ver que en la salida del primer flip-flop es de 4 Hz, la del segundo flip-flop es de 2Hz y él ultimo flip-flop 1 Hz.
4. Contadores con numero MOD <2N
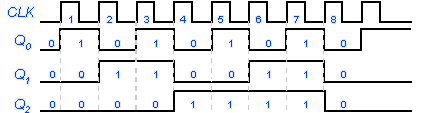
El contador básico puede ser modificado para producir números MOD menores que 2N permitiendo que el contador omita estados que normalmente son partes de la secuencia de conteo. Unos delos métodos para lograr esto se encuentra en la figura, donde se muestra un contador de rizos de 3 BIT, descartando la compuerta nand por un momento, podemos observar que el contador es un contador binario MOD 8 que contara en secuencia de 000 111. Sin embargo la presencia de la compuerta nand alterara esta secuencia como sigue:
La salida de nand se conecta a las entradas asíncronas reestablecer de cada flip-flop mientras que las salidas de nand sean altas, no tendrá efecto sobre el contador. Sin embargo cuando pase abajo borrara todos los flip-flop, de manera que el contador pase de inmediato al estado 000.
Las entrada de la compuerta nand son las salidas de los flip-flip Q1 y Q0, de manera que la salida nand pasara bajo siempre que Q1=Q0= 1 esta condición ocurrirá cuando el contador pase por el estado 101 al 110. El estado bajo en la salida nand inmediatamente borrara el contador al estado 000. una vez que se hallan borrado los flip-flop, la salida de nand retornaran a alto por que la condición Q1=Q0= 1 ya no existe.
La secuencia de conteo es por lo tanto.
| Q0 | Q1 | Q2 |
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
El estado 110 es un estado temporal que se necesita para limpiar el contador.
Aunque el contador pasa por estado 110 solo permanece hay unos cuanto nanosegundos, antes de reciclarse al 000, de este modo podemos decir esencialmente que este contador cuenta de 000 (0) 101 (5) y se recicla a 000.
En esencia, omite los estados 110 y 111 de manera que solamente pasa por 6 estados diferentes así se trata de un contador MOD 6.
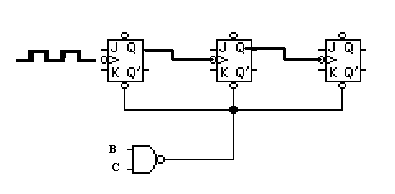
5. Variación del numero MOD.
El contador en la figura anterior es un MOD 6 debido a la elección de entradas en la compuerta nand. Se puede obtener cualquier numero MOD que se desee cambiando estas entradas. Por ejemplo si se emplea una compuerta nand e tres entradas, el contador funcionaria normalmente hasta llegar al 111, en este punto regresaría de inmediato al estado 000. ignorando la excursión temporal al estado 111 pasaría de 000 hasta 110, y luego regresaría a 000, produciendo un contador MOD 7.
6. Contadores de décadas o contadores BCD.
El contador MOD 10 se conoce también como contador de décadas. De echo un contador de décadas es cualquier contador que tenga 10 estados diferentes independientemente de la secuencia. Estos también se denominan contadores BCD para reiterar lo dicho cualquier contador MOD 10 es un contador de décadas y cualquier contador de décadas que cuenta en binario de 0000 a 1001 es un contador BCD.
Los contadores de década especialmente los de tipo BCD, se utilizan ampliamente en aplicaciones donde los pulsos o sucesos van a ser contados y los resultados exhibidos en algún tipo de dispositivo de visualización numérica decimal. Un contador de décadas a menudo se utiliza también para dividir una frecuencia de pulsos exactamente entre 10.
7. Contadores Asíncronos en CI.
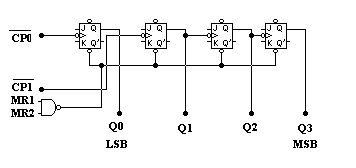
Existen varios contadores asíncronos en CI, tanto TTL como CMOS. Uno de ello es el TTL 74293. la figura muestra el diagrama lógico para el 74293. note los siguientes puntos:
El 74293 tiene cuatro flip-flop J-K con salidas Q0 Q1 Q2 Q3, donde Q0 corresponde al LSB y Q3 MSB. La distribución de los flip-flops es tal que el LSB se encuentra en el extremo izquierdo para satisfacer la convención de que las señales de entrada al circuito aparezcan a la izquierda.
Cada flip-flops tiene una entrada CP ( pulso de reloj) que es solo otro nombre para la entrada CLK, se puede tener acceso externo a las entradas de reloj para Q0 Y Q!, marcadas como CP0 Y CP1. la barras de inversión sobre estas entradas indican que se activan por un TPN.
Cada flip-flops tiene una entrada asíncrona borrar (CD). Estas se encuentran conectadas entre sí a la salida de una compuerta nand de dos entradas MR1 y MR2, donde MR denota reiniciación maestra. Ambas entradas MR deben estar altas para borrar el contador y ponerlo en 0000.
Los flip-flops Q1,Q2,Q3, ya están conectados como un contador de rizos de tres BIT, el flip-flops Q0 no esta conectado internamente a nada. Esto permite que el usuario opte por conectar Q0 a Q1 para formar un contador de 4 BIT o usar Q0 en forma separada si así lo desea.
8. Símbolo IEEE/ANSI para el contador 74293.
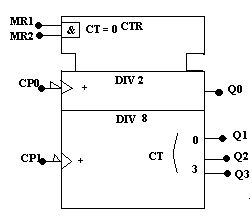
El símbolo contiene 3 bloques distintos. El bloque de la parte superior es el bloque común de control. La anotación CTR define este circuito integrado como un contador. Para el contador 74293, las entradas MR1 y MR2 son comunes para a todos los flip-flops del contador estas entradas MR1 y MR2 se muestran como entradas activas en alto combinadas internamente utilizando la operación la que esta indicada por la notación “&” esto indica que MR1 y MR2 deben encontrarse al mismo tiempo en estado activo, para reestablecer el contador. La notación CT = 0 indica que la acción de las entradas MR es hacer que la cuenta de salida sea igual a cero.
El bloque de en medio esta marcado con la etiqueta DIV 2 para señalar que este es un contador MOD 2 el cual claro esta es un solo flip-flops DIV 2 significa que el contador dividirá la frecuencia de reloj entre dos. El bloque de la parte inferior esta marcado con la etiqueta DIV 8 para señalar que este es un contador MOD 8. la anotación mas sobre cada entrada de reloj indica que la TPN del reloj ara que el valor de conteo se incremente en uno en otras palabras el contador cuenta en forma ascendente cada ves que se presenta una TPN. La notación menos se emplea para el contador descendente.
9. Contador asíncrono CMOS.
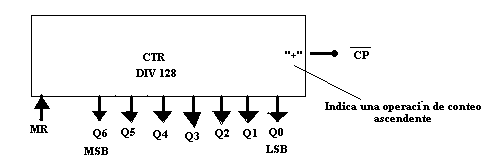
En la familia CMOS existen varios contadores asíncronos. La mayoría son equivalentes a las versiones TTL. Si embargo existen varios contadores asíncronos de CI que no tiene contraparte en la familia TTL, uno de ellos es 74HC4024. este CI es un contador de 7BIT con una entrada maestra de reestablecimiento asíncrono. Los 7 flip-flops están conectados internamente como un contador de rizos MOD 128. La entrada MR es activa en alto y puede emplearse para reiniciar todos los flip-flops hacia el estado cero.
10. Contador asíncrono descendente.
Es relativamente simple construir contadores asíncronos descendentes os cuales contaran hacia abajo desde una cuenta máxima hasta cero. ahora examinaremos la secuencia de conteo para un contador de tres BIT
| C | B | A | |
| (7) | 1 | 1 | 1 |
| (6) | 1 | 1 | 0 |
| (5) | 1 | 0 | 1 |
| (4) | 1 | 0 | 0 |
| (3) | 0 | 1 | 1 |
| (2) | 0 | 1 | 0 |
| (1) | 0 | 0 | 1 |
| (0) | 0 | 0 | 0 |
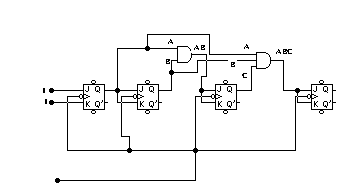
A, B y C representan los estados de salidas del flip-flops cuando el contador recorre su secuencia puede observarse que el flip-flop A es LSB cambia de estado en cada etapa de la secuencia, como hace en el contador ascendente. El flip-flops B cambia de estado cada ves que A pasa de bajo a alto; C cambia de estado cada ves que B pasa de bajo a alto, de este modo en un contado descendente cada flip-flops, excepto el primero debe complementarse cuando el flip-flops anterior pase de bajo a alto.
Los contadores descendentes no se utilizan tanto como los ascendentes. Su aplicación principal es en situaciones donde debe saberse cuando a ocurrido un numero deseado de pulsos de entrada. En estas situaciones el contador descendente se prefija al numero deseado y luego se le permite contar hacia abajo cuando se aplican los pulsos. Cuando el contador llega al estado cero es detectado por una compuerta lógica cuya salida indica que ha ocurrido el numero prefijado de pulsos.
11. Contadores síncronos paralelos.
El problema que se encuentra en los contadores de rizo es ocasionado por los retrasos acumulados en la propagación de los flip-flops dicho de otra manera no todos los flip-flops cambian en sincronía con los pulsos de entrada. Estas limitaciones pueden superarse con el uso de contadores síncronos o paralelos, en el que todos los flip flops se disparan en forma simultanea (en paralelo) por medio de los pulsos de reloj. Ya que los pulsos de entrada se aplican a todos los flip-flops debe utilizase algún medio para controlar cuando un flip-flops se dispare o permanezca inalterado por un pulso de reloj. Esto se logra utilizando la entradas J y K que en la siguiente figura para un contador MOD 16 de 4 BIT.
12. Contador síncronos descendentes y ascendentes.
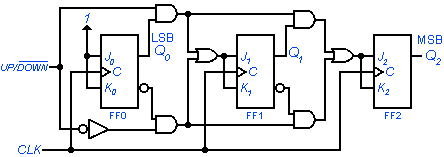
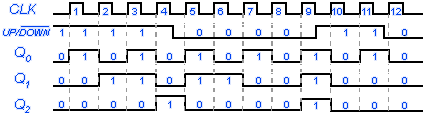
Los contadores ascendentes / descendente (up/down) también llamados contadores bidireccionales; son capaces de avanzar en cualquier sentido a lo largo de una secuencia definida y puede invertir su conteo en cualquier punto de su secuencia.
En el diagrama lógico se muestra un contador ascendente / descendente síncrono binario de tres bits diseñado a partir de flip-flops J-K en configuración toggle con disparo por borde de subida. Debido a que posee tres flip-flops, su ciclo básico se compone de ocho estados que van desde cero (000) hasta siete (111) en forma secuencial y repetitiva.
. 
13. Contadores con preestablecimiento.
Muchos contadores síncronos(paralelo) que están disponibles en CI están diseñados para ser prefijables; en otras palabras se pueden prefija r a cualquier valor inicial de conteo, ya sea en forma asíncrona (independientemente de la señal de reloj) o síncrona ( durante la transición activa de la señal de reloj) esta operación de prefijado también se conoce como carga del contador.
14. Preestablecimiento síncrono.
Muchos contadores síncronos paralelos de CI emplean el preestablecimiento síncrono con lo que el contador es prefijado durante la misma transición activa de la señal de reloj que se emplea para el conteo. El nivel lógico aplicado en la entrada determina si transición activa del reloj será la que preestablesca el contador o si esta será contada, como sucede durante el modo normal de operación.
15. Decodificación de un contador.
Los contadores digitales se utilizan frecuentemente en aplicaciones donde deben determinarse o exhibirse de alguna manera el conteo representado por los estados de los flip-flops uno de los medios más simples para exhibir el contenido de un contador consiste en conectar la salida de cada flip-flops a un diodo emisor de luz (LED). De esta manera, los estados de los flip-flops están representados por los led en forma visible ( encendido = 1, apagado = 0) y el conteo se puede determinar mentalmente al decodificador los estados binarios de los LED
. Por ejemplo, suponga que este método se ocupa para un contador BCD y los estados de las lámparas son apagado- encendido -encendido-apagado, respectivamente.esto representaría él numero binario 0110, que decodificaríamos mentalmente como el 6 decimal. Otras combinaciones de estados de los LED representarían los posibles conteos.
El método de LED indicador no es conveniente cuando aumenta el tamaño ( numero de BIT) del contador, porque es muy difícil decodificar mentalmente los resultados. Por esto es conveniente desarrollar un medio que decodifique electrónicamente el contenido del contador y mostrar los resultados de inmediato y que no requiera operaciones mentales
16. Descodificación activa en ALTO
Un contador MOD-X tiene x diferentes estados, cada uno es modelo en particular de ceros y unos almacenados en los flip-flops del contador. Este sistema es un circuito lógico que genera x diferentes salidas, las cuales detectan ciertos estados del contador. Las salidas del decodificador pueden diseñarse para introducir un nivel alto o uno bajo cuando ocurra la detección. Un decodificador activo alto genera salidas altas para indicar detección.
En la figura que veremos a continuación muestra la lógica completa de descodificación activa para un contador MOD-8. este cuenta de 8 compuertas and de 3 entradas, las cuales producen salidas altas para un estado en particular del contador.
Por ejemplo, la compuerta and 0 tiene como entradas las salidas del flip-flops C, B y A. Así su salida será baja en todos los tiempos, excepto cuando A =B=C=0, es decir en el conteo 000. análogamente, la compuerta and 5 tiene como entradas las salidas del flip-flops C,B y A, donde su salida pasara a alto solo cuando C = 1, B = 0 y A = 1; es decir, en el conteo de 101 ( 5 decimal ) . el resto de las compuertas and se comportan de la misma forma para los otros posibles conteos. En cualquier instante, solamente una compuerta de la salida and es alta, la que se decodifica para la cuenta en particular esta presente en el contador. Las formas de onda de la figura lo muestran claramente.
Las 8 salidas de and se pueden utilizar para controlar 8 indicadores LED por separado, lo que representa los números decimales del 0 al 7. solo la lámpara estará indicando el conteo adecuado


17. Descodificación activa en bajo
Si se emplean compuertas nand en lugar de and, las salidas detectoras producirán una señal alta, la que pasa abajo solo cuando ocurre él numero que se decodifica. Se utilizan ambos tipos de decodificadores, dependiendo del tipo de circuitos que sean conducidos por las salidas detectoras
18. Descodificación del contador BCD.
Este tiene 10 estados y se pueden decodificar usando las técnicas anteriores. Estos decodificadores ofrecen 10 salidas que corresponden a los dígitos del 0 al 9 representados por los estados de los flip-flops del contador. Las 10 salidas se pueden usar para controlar 10 indicadores eléctricos LED y tener una exhibición visual. Con mayor frecuencia en vez de utilizar 10 lámparas por separado, se utiliza un solo dispositivo para ver los números del 0 al 9, este se denomina tubo nixie, contiene 10 filamentos muy delgados que son la forma de cada uno de los números. El decodificador BCD controla que filamento esta encendido. Una clase más nueva de dispositivo decimales de exhibición visual contiene 7 pequeños segmentos hechos de un material (por lo general dispositivo de cristal liquido o LED ) que emite luz o reflejan la del medio ambiente. Las salidas del BCD controlan que segmentos están encendidos para producir un patrón que represente uno de los dígitos decimales.
20. Decodificaciones de salidas falsas.
Los retrasos entre las transiciones de los flip-flops pueden así mismo ocasionar problemas cuando se decodifica un contador de rizos. El problema se presenta en la forma de transiciones falsas( glitches) o espigas en las salidas de algunas de las compuertas de decodificación. Esto se ilustra en la siguiente figura para un contador de rizos MOD 4.
Las formas de ondas presentes en las salidas de cada flip-flops y compuertas de decodificación se muestran en la figura. Note el retraso de propagación que ocurre en las formas de onda de reloj y la salida A y entre las formas de onda A y B. Las transiciones falsas que ocurren en las formas de onda de decodificación X0 y X2 son ocasionadas por el retraso entre las formas de onda A y B. X0 es la salida de la decodificación de la compuerta and para l conteo normal 00.
La condición 00 también ocurre momentáneamente cuando el contador pasa del conteo 01 al 10 como lo demuestra la forma de onda. Esto se debe a que B no cambia de estado sino hasta que A pasa a bajo. Este estado momentáneo 00 solo dura algunos nano segundos pero puede ser detectado por la compuerta de decodificación si la respuesta de la compuerta es lo suficientemente rápida, por ello la espiga en la salida X0.
Una situación análoga produce una transición falsa en la salida X2. X2 es la decodificación para la condición 10 y ocurre momentáneamente en el instante en que el contador pasa de 11 a 00 en respuesta al cuarto pulso de reloj, como se muestra en la forma de onda. Una ves más esto se debe al retraso de la respuesta del flip-flops B depuse de que A a pasado a bajo.


21. Des habilitación estroboscópica.
Esta técnica emplea una señal llamada señal estroboscópica para mantener deshabilitadas las compuertas and de decodificación ( salidas en cero), hasta que todos los flip-flops hallan alcanzado un estado estable en respuesta a la transición negativa del reloj, esto se ilustra en la figura donde la señal estroboscópica se conecta como entrada a cada una de las compuertas de descodificación. Las formas de onda correspondiente muestran que la señal estroboscópica pasa a bajo cuando el pulso del reloj pasa a alto. Durante el tiempo en que la señal estroboscópica esta en bajo, las compuertas de decodificación se conservan en bajo. La señal estroboscópica se mantiene en bajo. La señal estroboscópica se va a alto para habilitar las compuertas de decodificación algún tiempo después de que el pulso de reloj se fue a bajo.
El método estroboscópico no se emplea si un contador solamente se utiliza con fines de exhibición visual, ya que las espigas en la decodificación son demasiado angostas para afectar la exhibición


22. Conexión en cascada de contadores BCD
Los contadores BCD se utilizan siempre que se vayan a contar pulsos y los resultados se exhiban en forma decimal. Un solo contador BCD puede contar de 0 a 9 y luego regresa a 0.
Para contar números decimales mayores, podemos conectar los BCD en forma de cascada como lo ilustrar la figura esta configuración opera como sigue:
Inicialmente todos los contadores son iniciados en el estado cero. Así la exhibición decimal es 0000.
Cuando llegan los pulsos de entrada el contador BCD avanza un conteo por pulso, después de que han ocurrido 9 pulsos los contadores BCD de centenas y decenas siguen todavía en cero y el contador de unidades esta en nueve( 1001 binario). De este modo la exhibición decimal se lee 0009.
En el décimo pulso de entrada el contador de las entradas se recicla a cero, ocasionando que las salidas que las salidas del flip-flops D vaya de 1 a 0, esta transición de 1 a 0 actúa como la entrada de reloj para el contador de las decenas y ocasiona que avancé un conteo. Así después de 10 pulsos de entrada, la lectura decimal es 010.
Cuando ocurren otros pulsos adicionales, el contador avanza un conteo por pulso y cada vez que el contador de unidades se recicla a 0 el contador de las decenas avanza 1 conteo. De este modo después de que han ocurrido 99 pulsos de entrada, el contador de las decenas esta en 9, al igual que el de las unidades. Así la lectura decimales 099.
En el pulso 100 de entrada, el contador de las unidades se recicla a 0, que a su ves ocasiona que el contador de las decenas se recicle a 0. así las salidas del flip-flops D del contador de las decenas realiza una transición de 1 a 0 que actúa como entrada de reloj para el contador de las centenas y ocasiona que avancé un conteo así después de 100 pulsos la lectura decimal es 100.
Este proceso continua hasta 999 pulsos. En el pulso 1000 todos los contadores se reciclan a 0.

23. Diseño de contadores síncronos.
Existen varios métodos para diseñar contadores que sigan secuencias arbitrarias, ahora presentaremos los detalles de un método que utiliza flip-flops J K conectados en configuración de contador síncrono la técnica es uno de los numerosos procedimientos de diseño que forma parte de una área del diseño de circuitos digitales que se llama diseño de circuitos secuenciales.
Idea básica:
En los contadores síncronos todos los flip-flops son disparado al mismo tiempo antes de cada pulso de reloj, las entradas J y K de cada flip-flops del contador deben tener el nivel correcto para asegurar que cada flip flop cambie Asia el estado correcto. El proceso de diseñar un contador síncrono se convierte en uno en que se diseña los circuitos lógicos que decodifican los diferentes estados del contador, para proporcionar los niveles lógicos en cada entrada J y K. Las entradas de estos circuitos decodificadores provienen de las salidas de uno o varios flip-flops.
Tabla de excitación J- K. La columna del extremo izquierdo de la tabla enumera las posibles transiciones en la salida de un flip-flops. La segunda y tercera columna contiene el estado presente, simbolizado como Q ( N ) y el siguiente estado simbolizado como Q ( N+1), para cada transición las ultimas dos columnas contienen los niveles J y K requeridos para producir cada transición a continuación examinamos cada caso.
Transición 0=> 0 el estado presente del flip-flops es cero y debe permanecer en cero cuando se aplica una entrada de reloj, de esta manera de entender como funciona un flip-flops J- K, esto sucede cuando J=K=0 ( condición de no cambio), o cuando J=0 y K = 1 (condición de borrado). De este modo J tiene que ser 0, pero K puede tener cualquier nivel. La tabla indica esto con un 0 en la columna correspondiente a J y una x en la columna para K. Recuerde que x representa una condición no importa.
Transición 0 =>1 este estado presente es 0 y cambia a 1, esto puede suceder ya sea cuando J=1 y K= 0 ( condición de establecimiento) o cuando J =K = 1 (condición de cambio de estado). De este modo J tiene que ser 1, pero para que esta transición ocurra K puede tener cualquier nivel.
Transición de 1=>0, el estado presente es 1 y debe cambar a 0. esto puede ocurrir cuando J = 0 y K = 1 o J=K=1. De este modo K tiene que ser 1 pero J puede estar en cualquiera de estos niveles.
Transición 1=>1, el estado presente es 1 y permanecerá en 1. esto ocurre cuando J=K=0 o J=1 y K = 0 así, K debe ser cero mientras J puede estar en cualquiera de estos niveles.
| Transición en la salida | Estado presente Q(N) | Estado siguiente Q(N+1) | J | K |
| 0=>0 | 0 | 0 | 0 | X |
| 0=>1 | 0 | 1 | 1 | X |
| 1=>0 | 1 | 0 | X | 1 |
| 1=>1 | 1 | 1 | x | 0 |
24. Contadores con registro de corrimiento
Contador de anillo: El contador de corrimiento más simple es un registro de corrimiento circulante conectado de modo que el ultimo flip-flops desplace su valor al primer flip-flops.
Esta configuración se muestra en la figura utilizando flip-flops de tipo D (también se puede usar flip-flops de tipo J K). Estos se conectan dé tal forma que la información se corra de izquierda a derecha, y de regreso de Q0 a Q3. En mucho casos solo hay un 1 en el registro y se hace que circule alrededor del registro en tanto se apliquen los pulsos del reloj. Por esta razón se le denomina contador de anillo.
Las formas de onda la tabla de secuencia y el diagrama de estados muestran los diferentes estados del flip-flops a medida que se aplica los pulsos, suponiendo que el estado inicial es Q3 =1 y Q2 = Q1 =Q0 = 0. después del primer pulso, el 1 a pasado de Q3 a Q2 de manera que el contador esta en el estado 0100. el segundo pulso produce el estado 0010, y el tercero produce el estado 0001. el cuarto pulso del reloj el estado 1 de Q0 se transfiere a Q3 lo que produce el estado 1000, que es desde luego el estado inicial. Los pulsos subsiguientes ocasionan que se repita la secuencia.
Este contador funciona como un contador MOD 4 por que tiene 4 estados distintos antes de que se repita la secuencia. Note que cada forma de onda de salida del flip-flops tiene una frecuencia igual a un cuarto de la frecuencia de reloj.
Un contador de anillo necesitara más flip-flops que un contador binario para el mismo numero MOD, por ejemplo un contador de anillo MOD 8 requiere de 8 flip-flops en tanto que un contador binario MOD 8 solo necesita 3.
A pesar de que es menos eficaz en el uso del flip-flops un contador de anillos sigue siendo útil debido a que puede ser decodificado sin tiene que emplear compuertas de decodificación. La señal de decodificación para cada estado se obtiene en la salida de sus flip-flops correspondientes.
Nota : los diagramas corresponden a un contador MOD 3.



25. Contador Johnson.
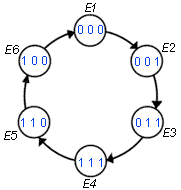
Aparte de los contadores binarios que pasan por todos sus posibles estados y de los de secuencia truncada, en los cuales el número máximo de posibles estados es 2n, donde n corresponde al número de flip-flops, existen contadores que tengan un número de estados determinado por la regla 2n, donde n es el número de flip-flops. Además estos contadores poseen una realimentación de la salida complementaria de la última etapa independiente del número de etapas del contador, a la entrada del primer flip-flop, dando como resultado una secuencia característica.
En el diagrama lógico se muestra un contador de Johnson ascendente de tres bits diseñado a partir de flip-flops Data con disparo por borde de subida. Debido a que posee tres flip-flops, su número máximo de estados es 6, con un ciclo básico que va desde cero (000) luego el contador se llenará de 1s de izquierda a derecha y luego se llenara de nuevo de 0s en forma repetitiva como se puede observar en el diagrama de tiempos.

. 
.

Conclusión.
-
Con el desarrollo de este trabajo se trato de explicar lo más simplemente posible todas las aplicaciones de los contadores, donde se puede saber como son los números MOD donde se designa la cantidad de flip-flops que se deben utilizar. También la forma de onda se disminuye a la mitad de la frecuencia de entrada en cada salida del flip-flop.
-
Otra forma es disminuir la cantidad de numero 2N mediante compuertas nand. Los contadores de décadas que son todos aquellos que tiene 10 estados.
-
Los contadores descendentes que son capaces de medir desde un numero máximo a un mínimo.
-
Los flip flops paralelos que tienen la capacidad de contar en forma simultanea.
-
Los ascendentes y descendentes tienen la capacidad de contar en ambos sentidos.
-
Los contadores con preestablecimiento a estos se les puede fijar cualquier valor inicial de conteo.
-
La conexión en cascada BCD es la conexión en forma que la información que se utiliza para el segundo flip-flops es sacada del primer, y del tercero del segundo y así sucesivamente. Esto se hace por que los BCD solo cuentan de 0 a 9, y para valores mayores se conectan en cascada.
-
Los distintos tipos de contadores como los de anillo y Jonson.
Electrónica
16
Descargar
| Enviado por: | Victor Julio |
| Idioma: | castellano |
| País: | Chile |
