Física
Composición de movimientos y leyes de Newton
ÍNDICE
Composición de movimientos Pag 2
- Objetivo Pag 2
- Material Pag 3
- Desarrollo Pag 3
- Anotaciones y cálculos Pag 6
- Conclusión Pag 7
COMPOSICIÓN DE MOVIMIENTOS
Objetivo:
La composición de movimientos se caracteriza por la posibilidad de separar en ejes el movimiento de un móvil cualquiera. Si se trata de un objeto lanzado en el seno del campo gravitatorio terrestre, será:
|
La ecuación de la trayectoria se obtiene, como recordaras, eliminando el tiempo entre "X" e "Y". Resulta: |
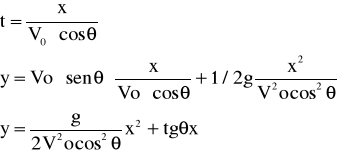
Si conocemos las variables Vo y ![]()
podríamos dibujar perfectamente la trayectoria. ¿Qué resultaría?
Sin embargo no es esto lo primero que haremos. Es muy importante que tengas en cuenta que variables de las que estamos manejando pueden obtenerse experimentalmente en el laboratorio. Por ahora el objetivo es:
| HALLAR "Vo" A PARTIR DE LAS MEDIDAS EXPERIMENTALES DE " |
Si manipulamos un poco la ecuación de la trayectoria:
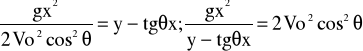
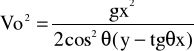
Material:-Rampa
-Pared
-Soporte
-Pinza
-Bola
-Metro
-Papel de calco
-Transportador
Desarrollo:
1. La rampa de caída de la bola ha de estar colocada en un ángulo fijo. Calcular ese ángulo mediante el Transportador, o a partir de alguna función trigonométrica. Señalar el punto de lanzamiento de la bola, que será siempre el mismo, lógicamente.
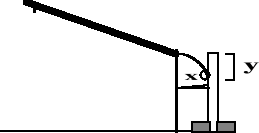
2. Perpendicular a ella y a unos 10 cm. del borde se dispone el obstáculo vertical o pared. Para detectar el impacto de la bola se ha adherido papel de calco encima del papel milimetrado o de un papel normal. El origen del papel es el punto en el que empieza el tiro oblicuo, allí donde acaba la rampa.
3. Con este montaje, el valor del desplazamiento horizontal (x) es la distancia entre el borde de la rampa y la pared. La y es la altura desde que la bola abandona la rampa. Alejando progresivamente la pared de la rampa se obtienen pares de valores (x, y). Es preferible hacer para cada x dos o tres lanzamientos; así, el valor de la ordenada es la media de los valores de y (y1, y2, y3) obtenidos para una "x" dada.
4. Si queremos precisar el valor de las coordenadas con toda exactitud, los valores han de tomarse de modo que el origen de coordenadas de las mediciones sea el centro de la bola y no el borde de la rampa.
5. A partir de los pares de valores obtenidos, se puede hacer una representación gráfica.
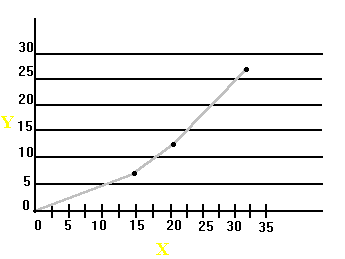
6. Disponiendo de los valores de x e y, asegurarse de que es correcto el valor de a y efectuar el cálculo para llegar a saber la velocidad inicial con que la bola abandona la rampa. Rellenar la tabla 2 y calcular el valor experimental de Vo (cinemática)
7. Si tenemos en cuenta algunas aproximaciones, podemos calcular Vo con facilidad. Por ejemplo:
La bola es una masa puntual (prescindir de rotación)
No hay rozamiento con la rampa.
Entonces: Ep(arriba) = Ec(abajo) y resulta: mgh = 1/2mv2.
![]()
8. Pero no es un cálculo preciso. No es aún el momento de analizar esto, pero si tenemos en cuenta efectos rotacionales en la bola, el resultado es mucho más exacto:
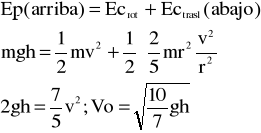
Y obtenemos así un valor distinto de Vo que se puede llamar Vo (energía). Parece lógico suponer que este valor es más preciso y adolece de menor error experimental que el otro. El % de diferencia entre uno y otro será:

Con todo ello rellena los datos de las tablas.
Anotaciones y cálculos:
TABLA 1
| X | Y1 | Y2 | Y3 | Ymedia |
| 0,205 m. | 0,127 m. | 0,128 m. | 0,128 m. | 0,1276 m. |
| 0,32 m. | 0,27 m. | 0,28 m. | 0,283 m. | 0,2776 m. |
| 0,145 m. | 0,73 m. | 0,68 m. | 0,7 m. | 0,7033 m. |
| X | 0,205 m. | 0,32 m. | 0,145 m. |
| Y | 0,1276 m. | 0,2776 m. | 0,7033 m. |
TABLA 2
| X | Y |
|
|
|
|
|
|
| 0,205 | 0,1276 | 0,9588 | 0,2962 | 0,4118 | 1,8386 | 0,0668 | 3,3529 |
| 0,32 | 0,2776 | 0,9588 | 0,2962 | 1,0035 | 1,8386 | 0,1858 | 2,9375 |
| 0,145 | 0,7033 | 0,9588 | 0,2962 | 0,2060 | 1,8386 | 0,6603 | 0,2439 |
| MEDIA:Vo= 1,87 m./sg |
TABLA 3
| H |
|
|
| 25,30 cm. | 1,88 cm./sg | 0,531 % |
Conclusión:
La experiencia ha valido la pena para aprender a situarnos en un laboratorio y he comprobado que lo hemos hecho mejor que hace unos meses.
Hay que tener cuidado al operar ya que si lo hacemos en cm. el valor de "g" es de 980 cm./sg y si no lo tenemos en cuenta todas las operaciones están mal hechas, por eso yo he decidido el pasar todas las distancias a metros (S. I.) para evitar problemas, pese a que ello suponga mayor dificultad en las operaciones.
También hay que tener cuidado con las mediciones para que el error sea mínimo.
El error que hemos cometido es relativamente pequeño y por lo tanto hemos creo que hemos hecho un buen trabajo.
La pena es, sinceramente, que nose vayan a repetir estas experiencias durante este año. Con el acentuante de que en C.O.U. no hay laboratorio
LEYES DE NEWTON
Objetivo:
El objetivo de esta experiencia es hallar la masa desconocida mediante la toma de pesos, tiempo y hallando la aceleración que adquiere el sistema, y por la fórmula de tensiones, despejamos la masa. Siempre teniendo en cuenta las leyes de Newton y sobre las que se construye toda la dinámica, en especial la segunda:
![]()
"Una fuerza aplicada sobre un cuerpo produce una aceleración proporcional a dicha fuerza"
Las demás leyes son:
"Si no actúan fuerzas sobre un cuerpo o su resultante es nula, el cuerpo permanecerá en estado de reposo o en movimiento rectilineo uniforme"
"Si un cuerpo ejerce una fuerza sobre otro, éste ejerce sobre el primero otra fuerza igual en módulo y dirección y de sentido opuesto"
El sencillo artilugio que nos va a permitir realizar la experiencia se llama máquina de Atwood y su resolución teórica es sencilla:
|
|
|
Si disponemos dos masas iguales en ambos brazos de la polea, no habrá movimiento. Si añadimos una pequeña masa, ésta descompasara todo el sistema que adquirirá una aceleración.
Resuelve ahora el problema tal como lo necesitas para llevar adelante la experiencia.
1. Datos cinemáticos para hallar "a". ¿Qué necesitas?
Altura "h"
Tiempo "t"
![]()
2. Sabiendo "a", ¿cómo podemos hallar "m", si ésa es nuestra incógnita?

Material: -Polea
-Hilo
-Pesas
-Metro
-Cronómetro
-Balanza
Desarrollo:
1. Construimos la polea y colocamos la masa incógnita en uno de sus ramales.
2. Se sitúan las pesas para que el recorrido sea máximo y el error mínimo. Al final del recorrido se sitúa un objeto metálico que suene al golpear la pesa.
3. Cronometramos repetidas veces el tiempo que le cuesta bajar a la pesa desde arriba del todo hasta el objeto metálico.
4. Al hallar la aceleración, con las ecuaciones halladas anteriormente podemos hallar la masa del sistema.
5. Comparamos el valor hallado con el real y hallamos el error.
Anotaciones y cálculos:
TABLA 1
| ALTURA | TIEMPO | T2 | aceleración |
| H=1,41m | 5,44s | 29,59s2 | 0,0952ms-2 |
| H=1,41m | 5,34s | 28,51s2 | 0,0988ms-2 |
| H=1,41m | 5,37s | 28,83s2 | 0,0977ms-2 |
| H=1,345m | 5,04s | 25,90s2 | 0,1038ms-2 |
| H=1,345m | 4,91s | 24,108s2 | 0,1115ms-2 |
| H=1,345m | 5,06s | 25,603s2 | 0,1050ms-2 |
| a media | a=0,1020ms-2 |
TABLA 2
| a exp | m exp | m real | % error |
| 0,1020ms-2 | 0,001093 Kg | 0,0017 Kg | 35 % |
Conclusión:
Esta experiencia es muy difícil de hacer porque los errores se cometen por todos los sitios. Primero la altura no sabemos si es perfecta. El tiempo está plagado de errores, ya que ni la salida ni la llegada son perfectas. Por último otro error es el de la polea que no le hemos dado rozamiento y a la cuerda no le hemos dado peso ni extensibilidad.
A pesar de todo esto el error comparado con los demás compañeros de la clase a sido bastante bueno.
Opciones:
Hemos repetido la experiencia añadiendo un peso de 2,5 gr.
| ALTURA | TIEMPO | T2 | ACELERACIÓN |
| 1,345 m | 4,53 sg | 20,52 | 0,1310 m/sg2 |
| 1,345 m | 4,59 sg | 21,06 | 0,1277 m/sg2 |
| 1,345 m | 4,47 sg | 19,98 | 0,1346 m/sg2 |
| Amedia= 0,1311 m/sg2 |
Como podemos comprobar al haber un peso mayor la aceleración también es mayor.
INFORME DE FÍSICA
Página 12
Descargar
| Enviado por: | Jorge Valls |
| Idioma: | castellano |
| País: | España |