Informática
Codificación de la Información
CODIFICACIÓN DE LA INFORMACIÓN
Para Lectura y Grabación de Audio en Compact Disc.
Códigos Correctores.
ÍNDICE:
1.- ¿Qué es el CD-da?.
Características Generales
Características Físicas del Disco.
Características del Sistema Óptico.
Características del Formato de la Señal
2.-¿Cómo se lee un CD-da?
¿Cómo se guarda la información?
Velocidad de transferencia de la información.
3.-CODIFICACIÓN
Errores Producidos
Pasos en la codificación:
-
Codificación CIRC.
-
Subcódigo.
-
Modulación EFM.
-
Bits de Unión.
-
Sincronización y formato de trama.
4.-Codificación CIRC a partir de códigos REED-SOLOMON
Codificación en Bloque
Códigos de Chequeo de Redundancia Cíclica
Distancia mínima de un código y Paridad.
Propiedades Genéricas de los cód. R-S
Bytes P y Q
Pasos de la codif. CIRC:
-
Retardo y Ordenación.
-
Codificación Reed-Solomon C2 (paridad Q).
-
Entrelazado.
-
Codif. Reed-Solomon C1(paridad P).
-
Retardo con inversión lógica de paridad.
1.- ¿QUÉ ES EL CD-Da?.
El sistema de audio digital basado en un soporte de Disco compacto, nació a mediados de 1982, por mediación de Phillips y Sony, dando vida a uno de los sistemas de almacenamiento con mayor capacidad, más fiabilidad y menor tamaño.
Inicialmente su uso fue unicamente el audio pero casi en paralelo se vislumbró su enorme utilidad, puesto que el audio era grabado en un formato digital de ceros y unos, ¿porque no usarlo para algo que usaba los ceros y unos mucho antes, como el tratamiento informático?, así pues el desarrollo para usar este soporte como almacenamiento fue materia de investigación y aplicación rápidamente estando hoy en dia estandarizado, y usado a nivel tanto profesional como meramente de usuario, y no solo para audio , o CD-ROM, sino para DVD, CD-i,CDV...
Características Generales
Como soporte para audio , el CD es capaz de almacenar en su formato estandar 74'33'', aunque en sus ultimas versiones puede llegar a lo 80', de audio hi-fi stereo.
Este formato estandar antes mencionado se encuentra en el Libro Rojo de Phillips y Sony y en el estandar BNN15-83-095.
Se basa en un sistema digital que requiere que la información a grabar sigua un muestreo y una cuantificación, y el medio es óptico porque la información se lee, (y se escribe) con un haz de luz, no como en los floppy (medio magnético) o en los antiguos LP (mecánico).
El sentido de giro de estos discos para su lectura y grabación es el contrario al de las agujas del reloj mirando la parte grabada.
Características Físicas del Disco
El disco tiene un diametro de 12 cm. un grosor de 1.2mm y pesa entre 14 y 33 gr.
y el diámetro del agujero central es de 15mm.
Como se ve en la figura 1, la base del disco es plástica, de policarbonato inyectado, material de que estan compuestos los cristales blindados, pero no es en esa capa donde se almacena la información, sino en otra finisima capa de aluminio (normalmente) de entre 50 y 100 nm de grosor, estsa capa es la que se deformará por medio de un haz de laser que impacta sobre ella y le produce unos pequeños bultitos que serán traducidos posteriormente en información digital.
Finalmente una capa de laca protectora por la parte que se leerá la información la protege de los arañazos, y mide entre 10 y 30 micrometros.
FIG.1
La información se reparte en pistas concentricas como las de un LP tradicional, estando separadas por 1.6 micrometros, haciendo un totalde 22188 pistas constituyendo una longitud de 5.7 Km . 60 de estas pistas de CD cabrían en la anchura de un surco normal de un vinilo.
Características del sistema óptico:
Longitud de onda estandar en el aire 780 nm y una anchura focal de +- 2um.
Carácterísticas del formato de señal:
El número máximo de cortes en el disco (tracs, canciones..) es 99.
La información se cuantifica linearmente a 16 bits y se muestrea con una frecuencia de 44.1kHz.
Se usa un código de corrección de errores CIRC (cross interleave Reed-Solomon Code) y un sistema de modulación ocho a catorce (EFM).
2.-¿Cómo se lee un CD?
Como se ha introducido se muestrea a 44.1 kHz, o lo que es lo mismo coge muestras de una señal electrica (en nuestro caso de audio) , 44100 veces por segundo, y utiliza el sistema binario para dar valores a cada una de estas muestras captadas, en concreto usa 216 niveles de codificación(16 bits), osea 65536 niveles discretos para representar la onda analógica que se muestrea (ver Fig. 2)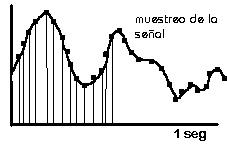
(44100 muestras)
Hagamos unos pequeños cálculos sobre el tamaño de la información que manejamos:
Si muestreamos la señal 44100 veces por segundo y para cada una de estas muestras necesitamos 16 bits, luego en cada segundo serán 705600 bits, y al tener un canal stereo supone lo mismo para el otro canal: 705600*2=1.411.200 bits por segundo, si a esto le sumamos los bits de corrección que veremos más adelante y una codificación EFM, se construyen unos paquetes de información que serán los escritos y leidos en el disco.
Estos paquetes aparecerán en el disco como pequeños bultos:
Cuando un grabador quiere introducir información en un disco, primero muestrea y codifica mediante un proceso que despues veremos, y finalmente obtiene un paquete de bits , que mediante un laser ira 'tallando' en la superficie metálica del disco, produciéndole unos pequeñisimos agujeros, o bultos (dependiendo de donde se mire). Estos bultos, tienen una anchura de 0.5um una altura de 0.13 um y una longitud de entre 0.8 y 3.1 um que será una propiedad del sistema de modulación de la señal.(ver Fig3).
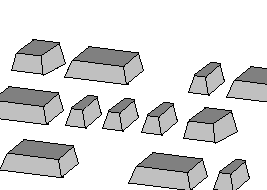
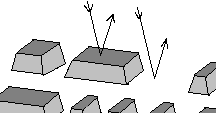
La lectura produce el efecto inverso, tendremos los bultitos en eldisco y el laser (en la lectura de menor potencia) irá recorriendo las pistas y mediante la reflexión de este rayo se sabrá si hay un bulto o un valle (por el desfase del rayo al rebotar en lo alto de un bulto o en la profundidad del valle). Supongamos que los bultos tienen una altura de 1/4 de la longitud de onda sobre el policarbonato, la luz reflejada que ha dado sobre un valle tardará más porque ha viajado más lejos que la que se refleje sobre un bulto que habrá rebotado antes, de hecho la que haya dado en un valle viajará 1/2 de long. de onda más que la del bulto
(1/4 +1/4). (Fig 4)
Teóricamente se crea una diferencia de fase entre estos dos rayos de luz , y se deberian anular un al otro, pero realmente, lo que ocurre es que los bultos se hacen menores de ¼ de la long. de onda, y el haz de laser es demasiado ancho para que la anulación sea total. Con todo esto la luz llega reflectada finalmente a un receptor óptico que lo convierte a señal eléctrica (analógica), ahora susceptible de ser tratada como señal de audio Hi-Fi estandar.
Contrariamente a como se podria pensar los bultos no definen los unos y ceros directamente, de hecho son los bordes de los bultos los que nos indican lo unos, y la longitud del area entre los bordes lo que nos indican los ceros.
2.2 Velocidad de Transferencia de la información:
El muestreo se hace a 44.1 kHz, obteniendo de cada muestra 32 bits, 16 del canal izquierdo y otros 16 del derecho. Por lo tanto, la fuente da datos a una velocidad de: 44.1 x 1000 x 32 = 1411200 bits/s o 172.26 kbytes/s. Esta sería la velocidad
de transferencia que tendrán los datos (la música) una vez leídos y decodificados en el
lector de CD-DA. Pero la unidad básica son 12 muestras de sonido (6 del izdo. y 6 del dcho) con lo que tenemos 12 muestras*16 bits=192 bits (24 bytes)
La velocidad de transferencia de la trama final del disco al lector es mayor, ya que en el mismo tiempo tenemos que enviar mucha más información. La trama se crea en todo el proceso de codificación que se explicará en los siguientes puntos. En este proceso se pasará de los 192 bits de datos iniciales a los 588 bits del formato final, de manera que la velocidad de transferencia de bits al lector hecha por el cabezal son 1411200 x 588 / 192 = 4321800 bits/s, o 527.5 kbytes/s.
3.- CODIFICACIÓN
Como se indicó en la anterior sección, se muestrean ambos canales a 44.1 kHz codificandose cada una de estas con 16 bits y ordenandolas anteponiendo la muestra del canal izdo al del dcho. Pero obviamente no se pueden grabar directamente esos bits a la superficie metálica, se necesitan unas técnicas para el control de los errores.Asi el proceso de grabación en un CD necesitará de una codificación y por tanto en el proceso de la lectura se hará la decodificación.
Existen dos tipos de errores que aparecen en el CD-Da:
*Errores aleatorios, que se producen y presentan aislados o en grupos de no más de 17 bits , un ejemplo común de esta clase es un bulto mal impreso en el disco.
*Errores de ráfaga que se presentan en grupos mayores de 17 bits, y pueden ser producidos por ejemplo por un arañazo en la superficie, que traspasa la capa protectora, o que simplemente desvia el laser que no lee el dato correcto.
Para conseguir la codificación final daremos unos pasos definidos:
a)Codificación CIRC (Cross Interleave Reed-Solomon Code)
Es un método de detección y corrección de errores que básicamente consiste en añadir unos bytes de paridad según la codif. Reed-Solomon. Este es el punto que más nos interesa y a el esta dedicado el siguiente punto donde será desarollado.
b)Subcódigo
Después de la codificación CIRC se añade un byte de subcódigo por bloque de 32 bytes.
Los 8 bits de subcódigo se llaman P, Q, R, S, T, U, V y W. El CD-DA sólo usa los bits P y Q. Estos bits de subcódigo incluyen información sobre el número de canciones del disco, su comienzo, final y duración, el copyright , etc. Los bytes de subcódigo se usan agrupando 98 bloques para obtener 98 x 8 = 784 bits.
d)Modulación EFM.
Lo que se pretende conseguir con esto es pasar a combinaciones de bits con pocas transiciones cero-uno para facilitar su grabación física en el disco.
EFM quiere decir modulación de ocho a catorce : los 33 bytes (=264 bits; 32 por bloque + 1 de subcódigo por bloque) escogidos en grupos de 1 byte (de 8 en 8 bits) se traducen a grupos de catorce bits, añadiendole 6 bits,el resultado lo que se llaman channel bits .
¿Qué factores se tienen en cuenta para escoger las palabras de 14 bits? debe minimizar el número de transiciones entre ceros y unos que es donde con mayor facilidad se darán los errores.
Para que los bultos y tierras tengan longitudes controladas, se exige que las palabras de 14 bits tengan más de 2 pero menos de 10 ceros seguidos. De las posibles 214=16384 combinaciones 267 satisfacen este criterio que serán las posibles palabras código pero sólo se necesitan 2 8 =256.
e)Bits de unión.
Los grupos de 14 bits se unen con 3 bits. Dos de los bits de unión son siempre 0, para
evitar tener unos sucesivos entre las palabras de 14 bits(por EFM). El tercer bit, que puede ser cero o uno, se añade para ayudar a la sincronización del reloj y para reducir los componentes de baja frecuencia de la señal digital. En la demodulación los tres bits se unión se desechan.
Cada bloque de la trama CIRC inicial(que tiene 32 bytes), al modularlo y añadirle los bits de unión, pasa a tener 17 bits más(14 bits al modular y 3 de bits de unión). Este grupo de 17 bits es el que se grabará en el disco.
Recordemos que los errores aleatorios estaban definidos como aquellos que como máximo tenían 17 bits. Es obvio entonces que un error aleatorio como máximo afectará a dos símbolos contiguos de 17 bits( el peor caso es que el error comience en el ultimo bit de un bloque y entonces afectará al siguiente bloque entero como máximo). El codificador CIRC retarda los bytes impares en 1 bloque como último paso antes de invertir las paridades P y Q (se verán a continuación). Así que al leer el disco, si se comete un error de 17 bits, después de la demodulación EFM y de desechar los bits de unión, los dos bytes contiguos se asignarán a bloques diferentes al ser retardados los símbolos pares. Por tanto como máximo, ante un error aleatorio, se pierde un byte por bloque. Si ocurre un error de ráfaga se perderán más bytes, y la paridad Q, en la medida de los posible, los corregirá.
f)Adición de la sincronización y formato de la trama.
Los grupos de 564 bits finales (33 x 14 channel bits + 34 x 3 bits de unión) resultantes deben ser diferenciados o delimitados unos de otros. Se usa por tanto una palabra de 24 bits de sincronización al inicio de cada grupo, que es única y no puede confundirse con ningún dato. La palabra en cuestión, a la que se habrá de añadir los bits de unión, es
1000 0000 0001 0000 0000 0010---> 3 transiciones separadas por 10 ceros. El formato de la trama final que se graba en el disco está formado por 588 bits: 24 bits de este sincronismo, y 564 bits de cada grupo como se ha visto antes.. Estos bits se imprimen en el policarbonato.
4.- CODIFICACIÓN CIRC A PARTIR DE CÓDIGOS REED-SOLOMON
Como hemos visto antes este es el primer paso que se da en la codificación y es el que vamos a ver más extensamente a continuación.
4.1 Codificación en Bloque.
Aquí los datos fuente son partidos en bloques de k bits de información y a los que el codificador convierte en un paquete de n bits, agregándoles (n-k) bits, que son llamados bits de redundancia, bits de paridad o bits de chequeo, y estos no aportan información
nueva.
Entre los códigos de bloque se mencionan los Códigos de Hamming, Códigos BCH y Códigos "Reed-Solomon" que son los que nos interesan.
(Los Códigos Cíclicos son una subclase de códigos lineales de bloque.)
4.2 Codigos de Chequeo de Redundancia Ciclica
Son la base de los CIRC a los que luego se les aplicará un entrelazado, que tratará de repartir la información con la idea de que, al reponer las muestras en sus posiciones originales los errores del disco quedarán repartidos entre los datos válidos, siendo muy probable corregirlos con los bytes de paridad.
Los codigos detectores de error son usados para la transmision de datos. El codigo polinomial, o codigo de chequeo de redundancia ciclica, CRC, es ampliamnete
usado con este fin. Se usa en los programas Z-modem, Pkunzip y Gzip...
Los codigos polinomiales se basan en el tratamiento de cadenas de bits como
polinomios con coeficientes 1 y 0 solamennte. Una cadena de k bits es considerada
como como la lista de coeficientes de un polinomio con k terminos, desde x 0 hasta
x k-1, es decir, un polinomio de grado k-1.El bit mas a la izquierda es el coeficiente
del termino de mayor orden. De esta manera si tenemos la cadena de bits de 6 bits,
110001, este se representara como x5+x4+x0.
El principio del CRC es el siguiente: La fuente que desea enviar un mensaje, una cadena
de m bits representada por un polinomio M(x), envia una trama que contiene a M(x)
con una cadena de chequeo al final, esta trama transmitida es el polinomio T(x). El
emisor del mensaje y el receptor del mismo deben conocer un Generador Polinomial, G(x), cuyos bits de mayor y menor orden deben ser 1. El polinomio transmitido es divisible por G(x), cuando el receptor toma a T(x), lo divide entre G(x) si el residuo no es cero, hubo algun error de transmision.
4.3 Distancia Mínima de un Código y Paridad:
La distancia mínima de un código es el número mínimo de símbolos que se han de cambiar en una palabra código para pasar de una palabra válida en nuestro alfabeto a otra tambien válida (no necesariamente contiguas).
Los elementos de paridad, como ya también sabemos son bits redundantes que se añaden a los datos y que a la hora de decodificarlos y según un criterio de paridad nos dirán si ha cambiado algún simbolo de la palabra código que se emitió. Veremos como utiliza CIRC estos conceptos.
4.4 Propiedades genéricas de los cód. R-S
Como se ha ido introduciendo los códigos Reed-Solomon son códigos de bloques lineales basado en la adición de bits de paridad y que permiten detectar y corregir los errores. Se basan en un area especial de las matemáticas llamado Campos Finitos, que tienen la propiedad de que operaciones aritméticas con elementos del campo, dan siempre un resultado en el campo. Los R-S deben implentar estas operaciones, ya sea de manera hardware o software.
Un código R-S viene especificado como RS(n,k) con s-bit simbolos. Esto significa que el codificador coge k simbolos de s bits cada uno y añade simbolos de paridad para hacer una palabra código de n simbolos. Hay n-k simbolos de paridad de s bits cada uno.
Un decodificador R-S podrá detectar y corregir hasta t simbolos que contienen error en una palabra código donde 2t=n-k.
Por ejemplo , un R-S muy conocido es RS(255,223) con simbolos de 8 bits. Cada palabra código contiene 255 bytes de los cuales 223 son de datos y consecuentemente 32 son de paridad. Entonces para este código:
n=255
k=223 --------> 2t=255-223 --->t=16
s=8
Con lo que el decodificador podrá corregir cualquier error de hasta 16 simbolos en la palabra código recibida.
Dado un tamaño de simbolo s la mayor longitud de palabra código (osea n) para un R-S es: n=2s-1
Por ej., la máxima longitud para una palabra con simbolos de 8 bits(s=8) es 255 bytes.
Los R-S pueden ser acortados haciendo un número de simbolos de datos cero y el codificador no los transmitirá, reinsertandolos en el decodif.
Ejemplo: RS(255,223) descrito antes puede ser acortado aRS(200,168). El codificador cogerá bloques de 168 bytes de datos, añadiendo 55 bytes de ceros, creará un codigo (255,223)pero solo transmitirá (200,168)
ERRORES EN SIMBOLOS: Un error de simbolo ocurrirá cuando 1 bit en el simbolo está mal o cuando todos los bits del simbol son erroneos.
Ej: en el RS(255,223) puede corregir 16 errores de simbolos. En el peor caso pueden ocurrir 16 bits de error, cada uno en un simbolo separado(byte), asi que el decodif. corrige 16 bits; en el mejor caso 16 bytes completos son erroneos así que corrige 128 bits
Particularmente los RS estan muy bien para corregir eroores de ráfaga(cuando una serie de bits en una palabra códigoo son erroneos), por eso es tan util en la codificación del CD.
Los códigos R-S algebraicos pueden corregir tanto errores como borrados. Un borrado se da cuando la posición de un simbolo erroneo es conocida. Un decodificador podrá corregir hsata t errores (como hemos visto) o hasta 2t borrados. La información del borrado suele se suministrada por la capa fisica de una red, por el demodulador en un sistema de comunicación digital.
Cuando una palabra código es decodificada hay tres posibilidades:
1.-Si 2s + r < 2t (s errores, r borrados) entonces el codigo transmitido originalmente será siempre corregido.
2.- SINO el decodificador detectará que no puede recuperarlo y lo indicará.
3.- O el decodif. decodificará una palabra código erronea y no indicará ningun hecho de error.
4.5 PASOS DE LA CODIFICACIÓNO CIRC:
El Cross Interleave Reed-Solomon Code como hemos visto es un método de detección y corrección de errores que consiste basicamente en añadir 8 bytes de paridad según la codificación Reed-Solomon. Esto se hará en dos pasos, llamados C1 y C2 (insertando 4 bytes en cada paso), separados por un entrelazado.
El cálculo de la paridad es idéntico en ambos pasos . La única diferencia reside en el número de bytes usados para obtener esa paridad. El C2 usa 24 Bytes (los 24 bytes que vimos que eran la información inicial . ver 2.2) y el C1 usa 28 bytes 24 del bloque inicial más 4 bytes de la paridad C2.
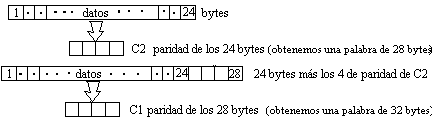
Con esto el CIRC consigue una probabilidad de error de 10-11 .
Entonces según vimos en el punto 4.4 tendremos un código Reed-Solomon RS(28,24) pues tenemos una palabra código de 28 bytes cuando realmente solo 24 son de datos, con esto podremos ver cuantos errores nos permite corregir.
como vimos: n=28 k=24 2t=n-k 2t=4 t=2 luego permite corregir hasta 2 bytes en una palabra. ¿como lo hace?:
Recordando la distancia mínima ( ver 4.3) veamos un ejemplo con dos palabras código
X1=000000
X2=111000 con 6 simbolos (aqui un simbolo es un bit).
Como se ve la Dmin=3
tenemos otras palabras código pero que son erroneas:
Y1=000001
Y2=100000 Si recibimos cualquiera de estos Yi sabremos que es un X1 incorrecto ya que solo varía un símbolo (1 bit) respecto a X1 pero 2 simbolos de X2. Es decir con Dmin=3 solo podemos conocer un simbolo erroneo por palabra, en general , si En indica el número de simbolos erroneos que se quieren corregir en una palabra nos lleva a:
Dmin=2Ne+1=Ne+(Ne+1). De esta expresión se deduce que la palabra leida incorrectamente (Yi) ha de estar a Ne simbolos de distancia de la correcta(X1) y a una distancia mayor que En de otra palabra legal del código(x2) como mínimo a Ne+1.
¿Cómo se pueden corregir 2 simbolos erroneos? Con Dmin=5, que es precisamente la que tiene la codif. R-S. En este caso los simbolos para nosotros van a ser bytes completos y no bits. Con lo que la palabra a la que añadirle le paridad es de 24 bytes (al añadir C2 queda con 28 bytes) o 28 Bytes (la coge al aplicar C2 y aplica su paridad 8 bytes más y deja la palabra con 32 bytes C1).Cada palabra sin paridad (24 y 28 bytes) legal, varia de una a otra en por lo menos 1 simbolo (1 byte). Asi que Dmin=1.
Es la paridad la que dará la distancia deseada:el R-S calcula los 4 bytes de manera que varien de una palabra a otra y den Dmin=5. Esto permite finalmente corregir 2 bytes en palabras de 28 y 32 bytes, que son las de 24 y 28 bytes más los 4 bytes de paridad.
Hay una posibilidad de corregir hasta 4 bytes usando Dmin=-1 deberemos conocer a priori la posición de los erroneos, es lo que hemos visto antes como borrados.
Veamos ahora los pasos completos de la codif CIRC
Retardo y Ordenación:
Primero se retardan las muestras pares de dos bloques. Cuando se habla de retardar muestras en n bloques se ha de entender que es un retardo de la señal digital de n x D , con D = 1 / [88200 (muestras / segundo)] x 12 (muestras / bloque) / [24 (bytes / bloque)] = 5.67 µs. Más adelante los bloques tendrán 28 y 32 bytes por la adición de paridad, números que han de sustituir a 24 en el anterior retardo.
El siguiente paso es un reordenamiento (simétrico entre las 6 primeras y las 6 últimas muestras) para separar las pares de las impares. Esto permite,en la decodificación,distribuir entre bytes correctos los bytes erróneos no corregibles con las paridades P (C1) y Q (C2) (pero marcados como erróneos por ellas) para su interpolación.
Codificación C2 (adición de la paridad Q).
Ahora los 24 bytes del bloque ordenado se usan para calcular 4 bytes de paridad, llamada paridad Q. La paridad Q está diseñada para corregir los errores de ráfaga marcados por la paridad P y también los errores aleatorios que no se pudieron corregir con ella. Los 4 bytes Q se sitúan en el centro de los 24 bytes del bloque primario para aumentar la distancia entre muestras pares e impares, y así mejorar la interpolación en caso de una ráfaga de errores. A este bloque de 28 bytes le llamaremos bloque codificado C2.
Entrelazado.
Después se hace un entrelazado cruzado: los 28 bytes que forman el bloque codificado C2 se retardan con diferentes períodos múltiplos de 4 bloques: el primer byte del bloque no se retarda, el segundo se retarda 4 bloques, el tercero 8 bloques y así hasta el byte vigésimo octavo, que se retarda en 108 bloques. De esta manera cada uno de los 28 bytes se almacena en otros tantos bloques distribuidos entre 109 bloques y los 28 bytes del bloque resultante proceden de 28 bloques codificados C2 diferentes. Este entrelazado está diseñado para, en la decodificación, aislar los errores de ráfaga, es decir, convertirlos en errores aleatorios. Al decodificar primero se usa la paridad P, se desentrelaza, y luego se usa la Q. Por tanto es la paridad Q la que puede corregir los
errores de ráfaga que en el paso anterior (el entrelazado) son convertidos en errores aleatorios.
Codificación C1 (adición de la paridad P).
De los 28 bytes resultantes se calculan 4 bytes más de paridad según CIRC C1. La paridad P corrige la mayor parte de errores aleatorios y detecta y aísla los errores de ráfaga para que los corrija la paridad Q. En el decodificador, si se detectan más errores, se marca todo el bloque con un erasure flag para que la paridad Q actúe sobre ellos (son los borrados).
Retardo con inversión lógica de paridad.
Los bytes impares se retardan en un bloque. Esto evita que los errores aleatorios corrompan más de un byte por bloque; como se ve un poco en la sección Bits de unión (4.2). Los bytes de paridad P y Q, como último paso, son invertidos lógicamente para tener siempre bytes diferentes de cero. Esto ayuda en la lectura de datos cuando hay zonas de silencio de audio. El bloque de 32 bytes resultante es la trama CIRC . Al que se le aplican , como se ve en 4.2, el subcódigo, la modulación EFM , los bits de unión, y la sincronización.
Para entender cómo funciona la corrección de errores en CIRC vamos a estudiar dos casos de lectura incorrecta de un bloque del disco: que se lean dos bytes contiguos erróneos (error aleatorio) y que se lean 23 bytes contiguos erróneos (error de ráfaga).
*Dos bytes erroneos: Después de leer la información del disco, de desechar los bits de unión y de demodular la EFM, el bloque de 32 bytes se retarda y se invierten las paridades. El retardo hace que los bytes dejen de ser contiguos y haya solo un error por bloque. El bloque pasa al decodificador C1. Al comprobar los bytes de paridad P detecta un byte erróneo. El byte podría ser un byte de paridad, sin merma de efectividad. Como hemos comentado antes, el código Reed-Solomon permite corregir hasta 2 bytes, así que corrige el byte detectado. El bloque se desentrelaza. En el decodificador C2 se quita la paridad Q y en el último paso se reordena y retarda, para obtener 24 bytes de datos correctos.
*23 bytes erroneos: En este caso, después del retardo tenemos un bloque con 11 bytes erróneos y otro con 12 bytes erróneos. El decodificador C1 detecta más de 2 bytes erróneos por bloque y marca cada bloque con un flag de borrado, sin poder corregirlos. Los bytes erróneos, por tanto, están indicados como tales para el resto de etapas. El desentrelazado es lo que ayudará a arreglar este panorama. Al desentrelazar los retardos que se aplican son los inversos que en el entrelazado, es decir, el primer byte se retarda 108 bloques, el segundo 104, y así hasta el último, que no se retarda. El resultado es que los bytes erróneos (marcados con un flag de borrado y por tanto en posiciones conocidas) quedan distribuidos entre bytes correctos, y los bloques resultantes tienen menos de 3 bytes erróneos, y son corregibles por el decodificador C2. Una pregunta natural surge: ¿hasta cuántos bytes erróneos contiguos se pueden corregir con CIRC? Hasta 16 bloques o 512 bytes. Cuando el error es mayor se opta por la interpolación de los bytes erróneos si éstos, que están marcados y por tanto en posiciones conocidas, se encuentran entre datos correctos. Si incluso la interpolación es imposible, el decodificador opta por pasar los bytes erróneos como silencio. Estos silencios suelen ser muy cortos y normalmente no son notados por el oido humano
CODIFICACIÓN DE LA INFORMACIÓN
Para Lectura y Grabación de Audio en Compact Disc.
Códigos Correctores.
Teoría de la Información y Codificación. 4º Ingeniería Informática
Fig.3 Bultos sobre la superficie de aluminio en el CD
Fig.4 Diferencia entre la reflexión del laser sobre un bulto o un valle
33 bloques de 17 bits =561 bits
33 bloques de 14 bits tras la modulación=462 bits
33 bloques de 8 bits=264 bits
Descargar
| Enviado por: | Pablo E Garcia |
| Idioma: | castellano |
| País: | España |
