Filosofía y Ciencia
Ciencia
1-Introducció: La teoria de la relativitat: especial i general
La teoria de la Relativitat va ser descoberta per Albert Einstein (1879-1955) el qual es pot considerar que ha estat el científic més eminent i revolucionari de tot el segle XX.
Abans d'aprofundir en la teoria mateixa, caldria matisar que Einstein feu dues teories sobre la relativitat: la restringida i la general. Aquestes dues no són independents sinó al contrari, complementàries, però que una tingué un objectiu i es feu en un any diferent que l'altra.
La teoria de la relativitat restringida (1905) va ser la primera, elaborada l'any 1905. Aquesta va fer un estudi que continuava d'alguna forma, la ciència de Galileu i Newton sobre el moviment rectilini uniforme però que al final acabà amb el mateix paradigma. Va descriure la física del moviment, doncs, en el marc dels sistemes de referència inercials, és a dir, aquells sobre els quals no actuen forces; estan en repòs o en moviment rectilini uniforme -amb acceleració 0-. Les seves implicacions van ser molt importants: a grans velocitats properes a la de la llum, sense poder superar-la, l'espai i el temps són relatius, és a dir que es dilaten.
Tot i així, aquesta teoria deixà fora del seu camp d'estudi i d'aplicació tota una sèrie de problemes físics com per exemple el de la gravitació o el del moviment dels cossos celests a l'univers ja que estaven en moviment rectilini uniformement accelerat. Va ser així quan Einstein, amb molt més temps i més feina elaborà la teoria de la relativitat general (1915). Aquesta segona doncs, fou la generalització de la relativitat especial o restringida, la qual permeté estudiar les relacions de transformació físiques entre sistemes de referència no inercials o sotmesos a l'acció d'una força.
Les geometries no euclidianes que van ser el seu instrument, serviren al científic alemany per a poder descriure totes les conseqüències que es deduïren de la construcció de la segona teoria de la Relativitat, la general. Per tant, el treball que es llegirà a continuació és sobre aquesta i l'altra es donarà per sabuda i entesa mínimament.
2-La teoria de la relativitat general
2.1-El principi d'equivalència
El principi d'equivalència havia estat ja descobert per la mecànica clàssica però aquesta no li havia donat la més mínima importància.
En ell, s'estableix una diferència entre la massa pesant d'un cos i la seva massa inercial; la gravitació actua sobre la primera, mentre que la segona es manifesta per la resistència que té un cos a un canvi de velocitat. La rigorosa proporcionalitat d'aquestes dues masses es posa en evidència per la igualtat d'acceleració en la caiguda lliure de dos cossos de diferent pes. És a dir, qualsevol sigui el pes d'un objecte que sempre serà accelerat a la mateixa velocitat per a la gravetat.
Aquest fet, tal com he comentat, no se'n donà més importància, en la mecànica newtoniana, que definir-la com una coincidència. Einstein en canvi, la va interpretar i en va deduir implicacions importantíssimes per a la relativitat general; la igualtat permetia establir l'equivalència, també, entre l'acceleració que actua sobre la massa inercial i l'acceleració gravitacional que actuen sobre la massa pesant.
Per resumir-ho seria bo d'explicar-ho a partir d'un exemple molt senzill:
Un científic es fica a dins d'una caixa en la qual no hi ha cap forat de tal manera que no pot veure què passa a l'exterior. Si tibéssin la caixa amb un fil a una velocitat considerable direcció amunt, el personatge de l'interior podria deduir dues conclusions lògiques i no contradictòries sobre el que li està passant:
.
Que una força externa que en podria anomenar gravetat, està tibant la seva caixa en una velocitat de 9 m/s -per exemple- cap avall. Això li explicaria d'una forma raonable perquè el terra de la caixa sembla que el vulgui “absorbir”.
La segona explicació i també raonable, seria la correcta en aquest cas. Hi ha una força externa que l'està tibant a una velocitat considerable cap amunt. D'aquesta manera també podria explicar els fenòmens que li passen a dins de la caixa.
Amb aquesta petita “metàfora” es pot comprovar el principi d'equivalència de la mecànica clàssica i la deducció que en va fer Einstein. Però per què li serví al científic prolífic? Doncs perquè, al voler generalitzar la teoria de la relativitat restringida, havia d'explicar els moviments accelerats i la gravetat n'era un d'ells. Havia d'explicar-la de nou, en el marc espacio-temporal, com a l'acceleració dels cossos celests.
2.2-La nova explicació del cosmos: l'univers espacio-temporal
Segons la teoria de la relativitat restringida, tal com he explicat a la introducció, l'espai i el temps, a grans velocitats i dimensions no són absoluts. En això estem parlant de velocitats properes a la llum i de masses astronòmiques tant com les dels planetes del sistema solar com immensament superiors.
Això és doncs el que passa segons Einstein a l'univers. El marc espacio-temporal quadrimensional- on el temps és la quarta coordenada del sistema tridimensional- es deforma a conseqüència de l'enorme quantitat de massa i energia concentrada en els cossos celests.
Aquestes equacions que calculen la curvatura de la deformació de l'espai-temps s'anomenen equacions de camp de la relativitat general. I són en aquestes on es genera la gravitació.
La distribució doncs, de l'energia i la massa dels cossos celests deformen l'espai-temps del cosmos de tal manera que el moviment dels altres astres amb menys massa i energia és a tendir als que en tenen més.

Einstein ho deduí en una formula matemàtica que relacionava la geometria de l'espai-temps quadrimensional -la no euclidiana- amb la distribució de la massa i l'energia: aquesta es coneix com l'equació d'Einstein i és el centre medul.lar de
la teoria de la relativitat general.
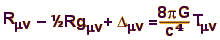
Aquesta equació de camp té al membre de l'esquerra una expressió matemàtica que caracteritza la curvatura de l'espai-temps. En el membre de la dreta es presenta una expressió que caracteritza la forma en què l'energia de massa es distribueix en aquest espai-temps , l'anomenat tensor d'energia-moment.
Ens diu doncs, si un espai-temps donat és compatible amb una distribució postulada d'energia de massa en aquest espai-temps.
L'espai es curva i, tot i que no ho analitzaré a fons, el temps es dilata. Això comporta que com més a prop estigui un objecte d'un cos celest grandiós més “a poc a poc” anirà el seu temps.
Fou així com Einstein va poder generalitzar la teoria de la relativitat restringida. Amb quantitats enormes de massa l'espai temps, com a enormes velocitats, es deforma de tal manera que genera la gravetat -la tendència dels cossos celests cap a d'altres que tenen moltíssima més quantitat d'energia de massa i han deformat molt més el seu espai-temps proper-.
2.3-Els efectes de la gravetat, entesa ara com a curvatura espacio-temporal
La pregunta que volgué respondre Einstein va ser aquesta: quina és la trajectòria dels cossos celests i com es pot explicar en el marc de la relativitat? La gravetat n'és la clau.
Es considera que els planetes descriuen trajectòries geodèsiques a l'espai-temps curvat per la presència d'un altre planeta més massiu. Per exemple en el cas del sistema solar, els planetes ho fan al voltant del sol.
Aquest fet pot explicar tant el moviment orbital de l'espai pla de Kepler com d'altres fenòmens que aquest científic del segle tal no va saber explicar com el fet que el periheli de Mercuri en el seu punt més proper al sol, avança 0.159 graus per segle.
Així doncs, en la relativitat general, fenòmens que la mecànica clàssica atribuïa a l'acció de la força de la gravetat -tals com una caiguda lliure de la orbita d'un planeta- són representats com moviments inercials en un espai-temps curvat.
2.3.1-Altres efectes de la gravetat:els forats negres
Tal com afirma la teoria de la relativitat general, segons la gravetat que genera un cos a l'espai fa que més o menys objectes tendeixin cap a ell. Doncs existeix un, que genera una gravetat suficientment forta perquè la llum no pugui escapar d'ell: el forat negre.
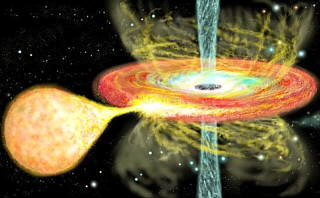
Partint de la teoria de la gravitació de Newton, que un objecte projectat en vertical cap amunt, escaparia de la Terra si la seva velocitat fos superior a 11km/s. Aquesta velocitat s'anomena d'escapatòria i cada planeta segons la seva gravitació en té una de diferent.
Doncs els forats negres tenen un camp gravitatori tant immens que ni la velocitat de la llum és suficient per a poder escapar d'ells.
2.3.2- Efectes de la curvatura de la llum
La llum es curva també quan passa prop d'un camp gravitatori curvat en l'espai-temps i això origina una sèrie de fenòmens tals com els lents gravitacionals - la curvació de la trajectòria de la llum provinent d'estrelles distants al passar a prop del sol, per exemple, de tal manera que es produeix un desplaçament aparent de les seves posicions reals-.
2.4- L'aplicació de les geometries no-euclidianes a la teoria de la relativitat general
Perquè fou necessari aplicar una altra geometria en comptes de l'euclidiana per a l'explicació de la relativitat general? Doncs perquè la primera, la que s'havia utilitzat majoritàriament durant tota la història des que va ser inventada, era per a espais plans. És a dir que tots els seus postulats són certs sempre i quan s'apliquin en espais amb curvatura nul.la.
El més controvertit dels sis postulats d'Euclides fou el que portà a la creació de les noves geometries anomenades actualment no-euclidianes. És l'axioma de les paral.leles, el cinquè, i s'anuncia així: Per un punt exterior a una recta es pot traçar una i única paral.lela.
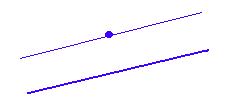
Tot començà en el plantejament que es feu Saccheri, un jueu del s.XIX, en els quatre angles d'un quadrat. Segons els postulats d'Euclides aquests havien de ser tots rectes és a dir, que medíssin 90 graus.
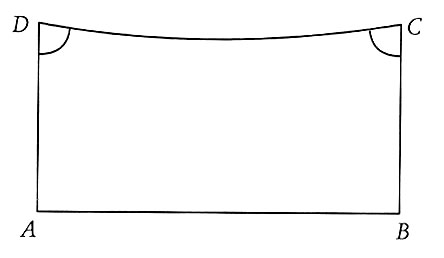
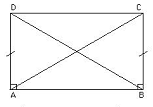
Saccheri es plantejà si els dos angles superiors o inferiors del quadrat podrien tenir més de 90 graus i ser obtusos o menys i ser aguts. En la primera il.lustració podem observar el segon cas en què els dos angles són aguts i en la segona la que sempre s'havia utilitzat, quan els dos angles són rectes.
A partir d'aquesta suposició nasqueren dues geometries no euclidianes: la de Lobachevsky en la qual s'utilitzava l'opció dels dos angles aguts i la de Riemann en la qual s'utilitzava l'opció dels dos angles obtusos.
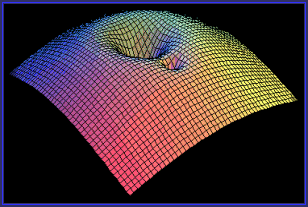
Einstein utilitzà per a calcular la curvatura espacio-temporal la de Lobachevsky ja que era la que calculava la curvatura negativa, la que es crea a conseqüència de les masses dels cossos celests. Si observem aquesta il.lustració podrem veure que la deformació (aquí només de l'espai perquè és una representació tridimensional) fa que la “reixeta espacial” es deformi i els quadrilàters que la componen ja no tenen els quatre angles rectes sinó dos d'aguts.
3-Conseqüències de la relativitat general
L'espai i el temps, en la mecànica clàssica concebuts com a recipients de la resta del món, és a dir, que eren absoluts on en ells i passava i s'hi esdevenia tot passen en Einstein a ser relatius i que per tant, ells també s'esdevenen com la resta d'elements del cosmos.
La gravetat deixa de ser una força d'atracció entre cossos inexplicable a ser la conseqüència de la deformació de l'espai-temps en una curvatura quadrimensional. Això implicà que tots els moviments dels cossos celests del sistema solar per exemple, en Newton descrits com a moviments el.líptics en un espai tridimensional i pla, passen a ser corbes geodèsiques en un espai quadrimensional i curvat.
L'instrument per al càlcul del nou sistema dinàmic de la gravetat canvia. Les geometries euclidianes d'un espai pla queden absoletes i passa a utilitzar-se les geometries no euclidianes dels espais de curvatura negativa.
En resum, s'acaba amb el paradigma Newtonià i la mecànica clàssica. Tot i així, cal esmentar que la teoria de la relativitat general va ser just el principi d'una nova cosmologia i visió de l'univers.
7
Descargar
| Enviado por: | Pauverda |
| Idioma: | catalán |
| País: | España |
