Ingeniero en Informática
Algoritmos
Equpamiento Usado
Las pruebas se hicieron en un computador marca Compaq deskpro, con procesador celeron de 500 mhz con 64 MB de ram.
Item 1
Planteamiento del Problema
Generar una tabla triangular de números binomiales hasta n=30, aplicando `Programación Dinámica' al algoritmo A1.
Análisis del problema
Al abordar el problema, primero ejecutamos el programa A1 chequeandolo hasta el número 30, luego realizamos el parche de programación dinámica basándonos en el algoritmo de fibonacci (visto en clases), con lo cual fue posible llegar a la solución de manera simple.
Análisis de la solución
La solución propuesta con la PD aplicada es la siguiente:
function binomial_d(n,k :numero):numero;
begin
if bino[n,k]=0 then
if (k=0) or (k=n) then
bino[n,k]:=1
else
bino[n,k]:=binomial_d(n-1,k)+binomial_d(n-1,k-1)
{endif};
{endif};
binomial_d:=bino[n,k];
end;
Con esta solución llegamos a los mismo resultados que el programa A1, pero con un tiempo de respuesta considerablemente menor.
La tabla generada es la siguiente:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15
1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120
1 17 136 680 2380 6188 12376 19448 24310 24310 19448 12376 6188 2380 680
1 18 153 816 3060 8568 18564 31824 43758 48620 43758 31824 18564 8568 3060
1 19 171 969 3876 11628 27132 50388 75582 92378 92378 75582 50388 27132 11628
1 20 190 1140 4845 15504 38760 77520 125970 167960 184756 167960 125970 77520 38760
1 21 210 1330 5985 20349 54264 116280 203490 293930 352716 352716 293930 203490 116280
1 22 231 1540 7315 26334 74613 170544 319770 497420 646646 705432 646646 497420 319770
1 23 253 1771 8855 33649 100947 245157 490314 817190 1144066 1352078 1352078 1144066 817190
1 24 276 2024 10626 42504 134596 346104 735471 1307504 1961256 2496144 2704156 2496144 1961256
1 25 300 2300 12650 53130 177100 480700 1081575 2042975 3268760 4457400 5200300 5200300 4457400
1 26 325 2600 14950 65780 230230 657800 1562275 3124550 5311735 7726160 9657700 10400600 9657700
1 27 351 2925 17550 80730 296010 888030 2220075 4686825 8436285 13037895 17383860 20058300 20058300
1 28 378 3276 20475 98280 376740 1184040 3108105 6906900 13123110 21474180 30421755 37442160 40116600
1 29 406 3654 23751 118755 475020 1560780 4292145 10015005 20030010 34597290 51895935 67863915 77558760
1 30 435 4060 27405 142506 593775 2035800 5852925 14307150 30045015 54627300 86493225 119759850 145422675
b) Calcular empíricamente la complejidad temporal del peor caso de A1.
Tenemos que :
Al realizar la regresión por mínimos cuadrados obtenemos la siguiente ecuación.
En el siguiente gráfico se muestra la comparación del la curva obtenida con los datos reales v/s la curva de los datos obtenidos con el modelo anterior.
Conclusión :
Se puede concluir que la programación dinámica para este tipo de algoritmos es una herramienta muy útil y necesaria, ya que con ello el rendimiento del algoritmo mejora considerablemente, además podemos indicar que el aplicar programación dinámica a este tipo de algoritmos es muy sencillo y que el caso del algoritmo A1 es muy similar al no muy bien ponderado fibonacci, ya que los tiempos que se demoran se dirige de acuerdo a una formula exponencial.
Item 2
Planteamiento del Problema
Calcular la probabilidad de ocurrencia de un árbol lineal de n nodos, n=0..30, definida por p=L(n)/B(n), donde:
![]()
y ![]()
B(0)=1, B(1)=1
a) Completar la tabla:
| N | L(n) | B(n) | P |
| 0 | 1 | 1 | 1,0000 |
| 1 | 1 | 1 | 1,0000 |
| 2 | 2 | 2 | 1,0000 |
| 3 | 4 | 5 | 0,8000 |
| 4 | 8 | 14 | 0,5714 |
| 5 | 16 | 42 | 0,3810 |
| 6 | 32 | 132 | 0,2424 |
| 7 | 64 | 429 | 0,1492 |
| 8 | 128 | 1.430 | 0,0895 |
| 9 | 256 | 4.862 | 0,0527 |
| 10 | 512 | 16.796 | 0,0305 |
| 11 | 1.024 | 58.786 | 0,0174 |
| 12 | 2.048 | 208.012 | 0,0098 |
| 13 | 4.096 | 742.900 | 0,0055 |
| 14 | 8.192 | 2.674.440 | 0,0031 |
| 15 | 16.384 | 9.694.845 | 0,0017 |
| 16 | 32.768 | 35.357.670 | 0,0009 |
| 17 | 65.536 | 129.644.790 | 0,0005 |
| 18 | 131.072 | 477.638.700 | 0,0003 |
| 19 | 262.144 | 1.767.263.190 | 0,0001 |
| 20 | 524.288 | 6.564.120.420 | 0,0001 |
| 21 | 1.048.576 | 24.466.267.020 | 0,0000 |
| 22 | 2.097.152 | 91.482.563.640 | 0,0000 |
| 23 | 4.194.304 | 343.059.613.650 | 0,0000 |
| 24 | 8.388.608 | 1.289.904.147.300 | 0,0000 |
| 25 | 16.777.216 | 4.861.946.401.500 | 0,0000 |
| 26 | 33.554.432 | 18.367.353.072.000 | 0,0000 |
| 27 | 67.108.864 | 69.533.550.916.000 | 0,0000 |
| 28 | 134.217.728 | 263.747.951.750.000 | 0,0000 |
| 29 | 268.435.456 | 1.002.242.216.700.000 | 0,0000 |
| 30 | 536.870.912 | 3.814.986.502.100.000 | 0,0000 |
b) Calcular empíricamente la complejidad temporal del algoritmo A1.
Modelo obtenido por regresión:
Conclusión :
Se puede concluir que para generar esta tabla se tuvo que aplicar programación dinámica al algoritmo, ya que el algoritmo B(n), se demoraba demasiado, ya que presenta el problema de ser exponencial, el problema para calcular los números desde n=20 hasta n=30 es que el resultado de b(n) son números demasiado grandes, lo cual no lo aguanta el tipo “longint”, entonces se tuvo que cambiar el tipo de número por “real”, entregando los resultados con notación científica, luego los transformamos en excel a una forma más legible y presentable.
Item 3
Planteamiento del Problema
Dados un arreglo a[1..n], de enteros positivos, y un entero k, determinar si existe un subconjunto de a[1..n] tal que su suma se k.
Calcule la complejidad temporal del peor caso de A1, empíricamente.
Se realizaron dos análisis de correlación provenientes del peor caso del algoritmo “existe”, este peor caso, se debiera dar cuando la suma de todos los a[n]=k, o cuando el algoritmo existe dé como resultado “false”.
Los análisis que se realizaron se hicieron comparando n desde 1 hasta 30 y uno corresponde al “tiempo” que se demora en ejecutarse el algoritmo, y el otro corresponde a la cantidad de llamadas que hace el algoritmo, arrojando los siguientes resultados:
Se puede determinar que la complejidad temporal de A1, se aproxima a una forma exponencial, es decir, la formula de recurrencia de este algoritmo sería:
![]()
Este resultado se dio en los dos tipos de análisis que se realizaron, análisis del tiempo de ejecución y análisis de la cantidad de llamadas que realiza el algoritmo, confirmando la fórmula propuesta.
Modelo obtenido por regresión :
Tiempo en CS :
Cantidad de Llamadas
Si k=57 y a=(20, 15, 18, 11, 17, 8, 16, 13, 10, 25, 6, 12, 14, 4, 7, 21) qué números escoge A1.
Análizamos los retornos de los valores y la pila de llamadas del algoritmo “existe”, y nos entregó los siguientes resultados:
| Retorno de los valores de existe | Lista de llamadas | |||||||
| k | N | a[n] | Existe | k | n | a[n] | ||
| 57 | 1 | 20 | FALSE | 1 | 57 | 16 | 21 | |
| 42 | 1 | 20 | FALSE | 2 | 57 | 15 | 7 | |
| 57 | 2 | 15 | FALSE | 57 | 14 | 4 | ||
| 39 | 1 | 20 | FALSE | 4 | 57 | 13 | 14 | |
| 24 | 1 | 20 | FALSE | 57 | 12 | 12 | ||
| 39 | 2 | 15 | FALSE | 57 | 11 | 6 | ||
| 57 | 3 | 18 | FALSE | 57 | 10 | 25 | ||
| 46 | 1 | 20 | FALSE | 8 | 57 | 9 | 10 | |
| 31 | 1 | 20 | FALSE | 57 | 8 | 13 | ||
| 46 | 2 | 15 | FALSE | 57 | 7 | 16 | ||
| 28 | 1 | 20 | FALSE | 57 | 6 | 8 | ||
| 13 | 1 | 20 | FALSE | 57 | 5 | 17 | ||
| 28 | 2 | 15 | FALSE | 57 | 4 | 11 | ||
| 46 | 3 | 18 | FALSE | 57 | 3 | 18 | ||
| 57 | 4 | 11 | FALSE | 57 | 2 | 15 | ||
| 40 | 1 | 20 | FALSE | 16 | 57 | 1 | 20 | |
| 25 | 1 | 20 | FALSE | 42 | 1 | 20 | ||
| 40 | 2 | 15 | FALSE | 39 | 2 | 15 | ||
| 22 | 1 | 20 | FALSE | 39 | 1 | 20 | ||
| 7 | 1 | 20 | FALSE | 24 | 1 | 20 | ||
| 22 | 2 | 15 | FALSE | 46 | 3 | 18 | ||
| 40 | 3 | 18 | FALSE | 46 | 2 | 15 | ||
| 29 | 1 | 20 | FALSE | 46 | 1 | 20 | ||
| 14 | 1 | 20 | FALSE | 31 | 1 | 20 | ||
| 29 | 2 | 15 | FALSE | 28 | 2 | 15 | ||
| 11 | 1 | 20 | FALSE | 28 | 1 | 20 | ||
| -4 | 1 | 20 | FALSE | 13 | 1 | 20 | ||
| 11 | 2 | 15 | FALSE | 40 | 4 | 11 | ||
| 29 | 3 | 18 | FALSE | 40 | 3 | 18 | ||
| 40 | 4 | 11 | FALSE | 40 | 2 | 15 | ||
| 57 | 5 | 17 | FALSE | 40 | 1 | 20 | ||
| 49 | 1 | 20 | FALSE | 26 | 25 | 1 | 20 | |
| 34 | 1 | 20 | FALSE | 22 | 2 | 15 | ||
| 49 | 2 | 15 | FALSE | 22 | 1 | 20 | ||
| 31 | 1 | 20 | FALSE | 7 | 1 | 20 | ||
| 16 | 1 | 20 | FALSE | 29 | 3 | 18 | ||
| 31 | 2 | 15 | FALSE | 29 | 2 | 15 | ||
| 49 | 3 | 18 | FALSE | 29 | 1 | 20 | ||
| 38 | 1 | 20 | FALSE | 14 | 1 | 20 | ||
| 23 | 1 | 20 | FALSE | 11 | 2 | 15 | ||
| 38 | 2 | 15 | FALSE | 11 | 1 | 20 | ||
| 20 | 1 | 20 | TRUE | -4 | 1 | 20 | ||
| 20 | 2 | 15 | TRUE | 49 | 5 | 17 | ||
| 38 | 3 | 18 | TRUE | 49 | 4 | 11 | ||
| 49 | 4 | 11 | TRUE | 49 | 3 | 18 | ||
| 49 | 5 | 17 | TRUE | 49 | 2 | 15 | ||
| 57 | 6 | 8 | TRUE | 49 | 1 | 20 | ||
| 57 | 7 | 16 | TRUE | 34 | 1 | 20 | ||
| 57 | 8 | 13 | TRUE | 31 | 2 | 15 | ||
| 57 | 9 | 10 | TRUE | 31 | 1 | 20 | ||
| 57 | 10 | 25 | TRUE | 16 | 1 | 20 | ||
| 57 | 11 | 6 | TRUE | 38 | 3 | 18 | ||
| 57 | 12 | 12 | TRUE | 38 | 2 | 15 | ||
| 57 | 13 | 14 | TRUE | 38 | 1 | 20 | ||
| 57 | 14 | 4 | TRUE | 23 | 1 | 20 | ||
| 57 | 15 | 7 | TRUE | 20 | 2 | 15 | ||
| 57 | 16 | 21 | TRUE | 20 | 1 | 20 |
Como podemos ver, al ejecutar el algoritmo con las condiciones propuestas en el planteamiento de la pregunta, podemos observar que el algoritmo hace 57 llamadas, lo cual proviene de 1+2+4+8+16+26, donde el 26 corresponde a la cantidad de llamadas que ocupó el algoritmo al encontrar el útlimo número de la combinación de sumatorias para que k=57, como para esto no fue necesario recorrer el resto de combinaciones, el algortimo no alcanza a hacer el número de combinaciones propuesto en la formula general del peor caso.
Se observa además en la matriz del retorno de valores que el n=6 solo aparece una vez, en el llamado recursivo inicial, lo cual indica que el algoritmo se devuelve al analizar las combinaciones dicho n, la cual corresponde al número 8.
Como se aprecia los números que toma el algoritmo “existe”, están marcados con negrita en la lista de llamadas, y estos números son:
20, 18, 11, 8.
Item 4
Planteamiento del Problema
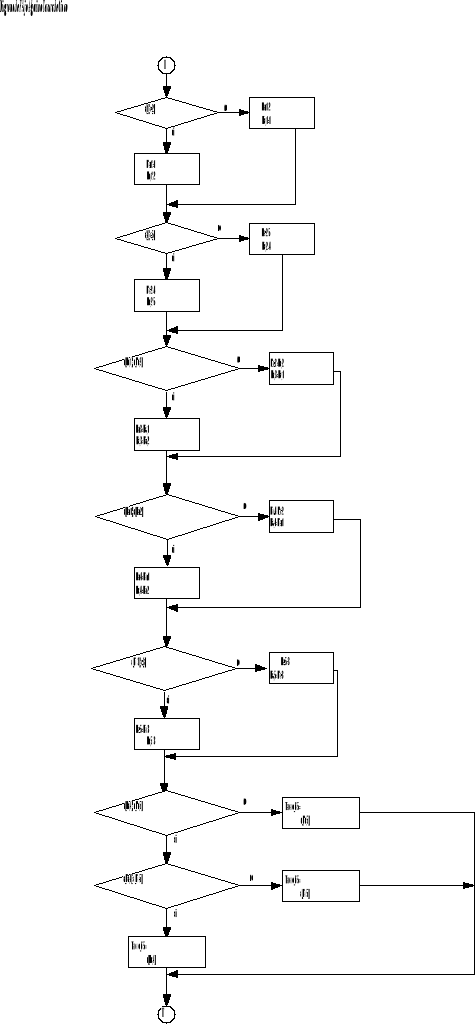
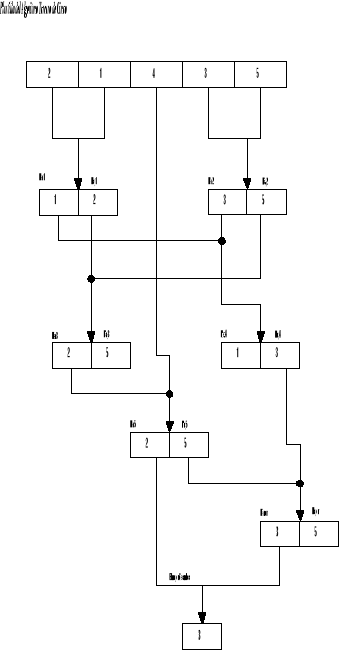
Diseñe un algoritmo directo A1, TerceroDe5, que determine el tercer elemento mayor en un arreglo NO de cinco elementos y tal que tp(A1)"7.
Análisis del problema
Al abordar el problema, nos dimos cuenta que en realidad el problema que se presenta no es trivial, ya que nos tiende a confundir, debido a la cantidad de comparaciones que existen, por lo cual decidimos crear un plantilla, basada en el algoritmo torneo, después de varias pruebas llegamos a la que se muestra en la figura.
Según la plantilla propuesta el determinar el tercero de cinco elementos, se puede hacer con 6 o algunas veces con 7 comparaciones resolviendo el problema propuesto.
Análisis de la solución
Según esto se generó el siguiente diagrama de flujo que muestra en forma más entendible la solución propuesta.
El algoritmo propuesto escrito en lenguaje pascal es el siguiente:
function Tercero_de5(var a:Arreglo_de5) : integer;
var may1, may2, may3, may4, may5, men1, men2, men3, men4, men5 : integer;
begin
if (a[1]<a[2]) then
begin
men1:=1;
may1:=2;
end
else begin
men1:=2;
may1:=1;
end;
if (a[4]<a[5]) then
begin
men2:=4;
may2:=5;
end
else begin
men2:=5;
may2:=4;
end;
if (a[may1]<a[may2]) then
begin
men3:=may1;
may3:=may2;
end
else begin
men3:=may2;
may3:=may1;
end;
if (a[men1]<a[men2]) then
begin
men4:=men1;
may4:=men2;
end
else begin
men4:=men2;
may4:=men1;
end;
if (a[men3]<a[3]) then
begin
men5:=men3;
may5:=3;
end
else begin
men5:=3;
may5:=men3;
end;
if (a[may4]<a[may5]) then
if (a[may4]>a[men5]) then
Tercero_de5:=a[may4]
else
Tercero_de5:=a[men5]
else
Tercero_de5:=a[may5];
end;
Conclusión :
Se puede concluir que el algoritmo presentado determina el tercer elemento de una arreglo de cinco elementos con tiempo peor igual a 6 o algunas veces siete comparaciones, este algoritmo se comprobó con 1000 datos de pruebas gnenerados al azar, arrojando siempre el resultado esperado.
Item 5
Planteamiento del Problema
Mejore el algoritmo A1: Function B(n): numero; usando programación dinámica. Calule empiricamente la complejidad del peor caso del algoritmo modificado.
Análisis de la solución
La solución propuesta con la PD aplicada es la siguiente:
function b_d(n:longint) :numero;
var s:numero;
k:longint;
begin
if (arre_nodo[n]=0) then
if (n=0) then
arre_nodo[n]:=1
else
begin
s:=0;
for k:=0 to n-1 do
s:=s+b_d(k)*b_d(n-k-1);
arre_nodo[n]:=s;
end{if};
b_d:=arre_nodo[n];
end;
Conclusión :
Se puede concluir que la programación dinámica para este algoritmo, como la fue también para el binomial mejora considerablemente el tiempo de respuesta del algoritmo, ya que para cualquier valor de n el tiempo de ejecución fue siempre 0 (cero) Centesimas de Segundo , eso sí tuvimos el inconveniente, que el lenguaje sólo nos permite calcular el B(n) hasta n=59, ya que después de esto se cae debido a que el número generado es demasiado grande, no soportandolo el lenguaje.
Prueba #2
Análisis de Algoritmos
12
![]()
![]()
![]()
![]()
![]()

Descargar
| Enviado por: | Osvaldo Miranda Y Cristian Ruiz |
| Idioma: | castellano |
| País: | Chile |
