Informática
Algoritmos genéticos
ALGORITMOS GENÉTICOS
1 Búsqueda, optimización y aprendizaje
En realidad, los algoritmos de búsqueda abarcan prácticamente todo algoritmo para resolver problemas automáticamente. Habitualmente, en Informática se habla de búsqueda cuando hay que hallar información, siguiendo un determinado criterio, dentro de un conjunto de datos almacenados; sin embargo, aquí nos referiremos a otro tipo de algoritmos de búsqueda, a saber, aquellos que, dado el espacio de todas las posibles soluciones a un problema, y partiendo de una solución inicial, son capaces de encontrar la solución mejor o la única. El ejemplo clásico de este tipo de problemas se encuentra en los rompecabezas y juegos que se suelen abordar en inteligencia artificial. Un ejemplo es el problema de las 8 reinas, en el cual se deben de colocar 8 reinas en un tablero de ajedrez de forma que ninguna amenace a otra; o las torres de Hanoi, en el que, dada una serie de discos de radio decreciente apilados, hay que apilarlos en otro sitio teniendo en cuenta que no se puede colocar ningún disco encima de otro de radio inferior.
Este tipo de problemas es fácil de abordar usando algoritmos "clásicos", como por ejemplo algoritmos recursivos o de tipo voraz (greedy), sin embargo, hay otro tipo de problemas mucho más complicados, sobre todo los NP-completos (aquellos cuya complejidad crece con el tamaño del problema de forma exponencial) que no pueden ser abordados de esta forma. Algunos ejemplos de estos problemas serían los siguientes:
-
8-puzzle, en el cual, como se muestra en la ilustración 1, a partir de una configuración inicial donde hay 8 cuadros desordenados, hay que llegar a otra configuración donde estén ordenados, usando para el intercambio cualquier posición que se halle vacía. El problema de búsqueda en este caso consiste en encontrar un camino que vaya desde la configuración inicial hasta la final.
-
Problema del viajante, en el cual, dadas una serie de ciudades separadas por distancias diferentes, hay que calcular un camino tal que la distancia total recorrida sea mínima, y no que no repita ninguna ciudad. Este problema es NP-completo, y es paradigmático de este tipo de problemas.
-
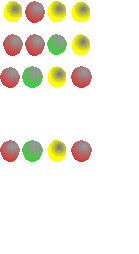
Mastermind: En este juego, que se muestra en la figura 2, un jugador debe de averiguar una combinación de chinchetas de colores oculta por el otro jugador, y lo hace haciendo suposiciones sobre la combinación, y siendo contestado con una chincheta pequeña y blanca por cada acierto de color, y una negra por cada acierto de color o posición. Sólo una solución (entre 64) es la correcta, pero el jugador que ha puesto la combinación oculta va orientando la búsqueda mediante las chinchetas blancas o negras. El problema se hace exponencialmente más difícil cuando se aumenta el número de colores, y la longitud de la combinación.
En muchos casos, la búsqueda está guiada por una función que indica lo buena que es esa solución, o el coste de la misma, o lo cerca que se está de la solución final, si es que se conoce; el problema se convierte entonces en un problema de optimización, es decir, encontrar la solución que maximiza la función objetivo, de evaluación o fitness o minimiza el coste. En términos formales, dada una función F de n variables x1,x2,..., xn, optimizar la función consiste en encontrar la combinación de valores de xi tales que F(x1, x2,..., xn) = Máximo. Se puede hablar de maximizar en vez de minimizar sin perder generalidad, ya que maximizar F equivale a minimizar -F.
Generalmente, los problemas de optimización son tratados por la rama de las matemáticas denominada Investigación Operacional, aunque prácticamente todas las ramas de la ciencia y la ingeniería necesitan tratar con problemas de optimización en algún momento. Por ejemplo, en teoría de juegos se trata de maximizar la probabilidad de ganar, y en reconocimiento de patrones de minimizar el error de clasificación de un patrón desconocido (como una imagen de satélite digitalizada, o un canal procesado de una señal de un electroencefalograma).
El problema de optimización no siempre está formulado de una forma tan clara. En muchos casos, la forma de la función F no se conoce, y debe de aproximarse mediante polinomios o combinaciones de funciones conocidas; habría entonces que hallar los coeficientes de los polinomios o funciones que hacen que la función calculada se acerque lo más posible a la función objetivo. Cuando el problema se reduce a calcular una serie de coeficientes, se habla de optimización paramétrica.
En control industrial se plantean también problemas de optimización: cómo mantener el funcionamiento de una máquina dentro de su régimen óptimo, por ejemplo. Cada máquina suele tener una serie de parámetros variables, y lo que se desea optimizar es habitualmente la calidad del producto final o la rapidez a la hora de producirlo.
En algunos casos, la función de evaluación ni siquiera existe, o no es estática, sino que viene dada por el entorno de la solución. Por ejemplo, en un programa para jugar al Othello o reversi, el fitness vendrá dada por su puntuación a la hora de jugar con los demás jugadores. Un autor, Pollack hizo enfrentarse a unas estrategias de juego con otras, de forma que según van evolucionando, el fitness va variando. Este tipo de optimización se suele encontrar en problemas de vida artificial y el Dilema del Prisionero, usado para modelizar interacciones sociales.
El dilema del prisionero iterado es un juego en el cual se enfrentan dos jugadores, que representan dos presos en una cárcel, que se han puesto de acuerdo para fugarse; en cada iteración, cada jugador decide si se chiva al director de la cárcel, o coopera con el otro y se escapa. Si los dos cooperan, reciben una recompensa de 3; si uno de los dos se chiva, recibe todos los privilegios de un preso bueno en la forma de una recompensa de 5, y si los dos se chivan, reciben una recompensa, pero mucho menor, como aparece en la tabla. Si este juego se repite por un número finito y conocido de iteraciones, la estrategia óptima es siempre chivarse, porque consigues una recompensa asegurada de 1*número de jugadas, sin embargo, a largo plazo la estrategia óptima es cooperar, porque la recompensa es de 3. Con este juego se han hecho muchas variantes; un algoritmo debería de crear una estrategia de forma que maximice la recompensa de un jugador.
En los problemas de Biología que la Vida Artificial trata de resolver mediente simulaciones, el fitness viene siempre dado por el entorno, acercándose a la definición biológica de fitness, que no es otra cosa que el número posible de descendientes de un individuo (que no siempre es el mismo que el número real de descendientes).
En algunos se trata de optimizar F(C), donde C es una combinación de diferentes elementos que pueden tomar un número finito de valores; pueden ser combinaciones con o sin repetición, o incluso permutaciones, como en el caso del problema del viajante; en este caso se denominan problemas de optimización combinatoria.
No siempre, el espacio de búsqueda completo contiene soluciones válidas; en algunos casos, los valores de las variables se sitúan dentro de un rango, más allá del cual la solución es inválida. Se trata entonces de un problema de optimización con restricciones. En este caso, el problema consiste en maximizar F(xi) dentro del subespacio. Un ejemplo de este problema es el de optimización de los horarios de clase de una institución de enseñanza; hay que disponerla de forma que un profesor no deba estar en dos sitios a la vez (un alumno, puede), que el número de horas libres entre clases sea mínimo, y que se cumplan las preferencias de todos los implicados. En este caso, la optimización se reduce a cumplir todas las restricciones.
Otro ejemplo clásico es el denominado job-shop scheduling, o disposición de una línea de montaje, en donde cada componente de la línea debe de estar ocupado el mayor tiempo posible y cumplir restricciones de tiempos de entrega,
Hay muchas formar de abordar problemas de optimización. Algunas de ellas se verán en las siguientes secciones
1.1 Método analítico
Si existe la función F, es de una sola variable, y se puede derivar dos veces en todo su rango, se pueden hallar todos sus máximos, sean locales o globales. Sin embargo, la mayoría de las veces no se conoce la forma de la función F, y si se conoce, no tiene porqué ser diferenciable ni siquiera una vez. Incluso el tratamiento analítico para funciones de más de 1 variable es complicado.
1.2 Métodos exhaustivos, aleatorios y heurísticos
Los métodos exhaustivos recorren todo el espacio de búsqueda, quedándose con la mejor solución, y los heurísticos utilizan reglas para eliminar zonas del espacio de búsqueda consideradas "poco interesantes". Algunos algoritmos de búsqueda, como el MiniMax, son de este tipo; se suelen utilizar en juegos para examinar y podar el árbol de posibilidades a partir de la jugada actual; Deep Blue, por ejemplo, juega de esta forma.
En los métodos aleatorios, se va muestreando el espacio de búsqueda acotando las zonas que no han sido exploradas; se escoge la mejor solución, y, además, se da el intervalo de confianza de la solución encontrada.
1.3 Hillclimbing,
En estos métodos se va evaluando la función en uno o varios puntos, pasando de un punto a otro en el cual el valor de la evaluación es superior. La búsqueda termina cuando se ha encontrado el punto con un valor máximo. En general, un algoritmo escalador funciona de la forma siguiente
Estos algoritmos toman muchas formas diferentes, según el número de dimensiones del problema solución, el valor del incremento y en la dirección en la cual se tiene que dar. En algunos casos se utiliza el llamado Método Montecarlo (por el casino), en el cual se escoge la nueva solución de forma aleatoria.
El principal problema de este tipo de algoritmos es que se quedan en el pico más cercano a la solución inicial; además, no son válidos para problemas multimodales, en los cuales la función de coste tiene varios óptimos posibles.
1.4 Recocimiento simulado
Conocido como Simulated Annealing, en inglés, el nombre viene de la forma como se consiguen ciertas aleaciones en forja; una vez fundido el metal, se va enfriando poco a poco, para conseguir finalmente la estructura cristalina correcta, que haga que la aleación sea dura y resistente.
Este algoritmo se podría calificar como escalador estocástico, y su principal objetivo es evitar los mínimos locales en los que suelen caer los escaladores. Para ello, no siempre acepta la solución óptima, sino que a veces puede escoger una solución menos óptima, siempre que la diferencia entre ambos tenga un nivel determinado, que depende de un parámetro denominado temperatura (seguimos con la metáfora). El algoritmo de recocimiento simulado es el siguiente:
1.5 Técnicas basadas en población
Este tipo de técnicas pueden ser versiones de cualquiera de las anteriores, pero en vez de tener una sola solución, que se va alterando hasta obtener el óptimo, se persigue el óptimo cambiando varias soluciones; de esta forma es más fácil escapar de los mínimos locales tan temidos. Entre estas técnicas se hallan la mayoría de los algoritmos evolutivos, que es donde vamos a centrar nuestro trabajo.
1.6 Técnicas experimentales
En algunos casos, solo el ojo humano es capaz de evaluar lo apropiada que es una solución a un tema determinado, por ejemplo, en problemas de diseño o de calidad. En este caso, se pueden utilizar cualquiera de las técnicas expuestas anteriormente, pero a la hora de evaluar una solución, un experto o experta tendrá que darle una puntuación. Por ejemplo, es lo que se usa cuando uno se prueba ropa para dar con la combinación correcta de colores y estilos.
2 La evolución
Después de ver el tipo de problemas a los que se pueden aplicar los algoritmos evolutivos, se va a estudiar qué es lo que inspira dichos algoritmos, la Naturaleza, ese fenómeno natural denominado evolución, y si optimiza o no.
La teoría de la evolución (que no es tal teoría, sino una serie de hechos probados), fue descrita por Charles Darwin. La hipótesis de Darwin, presentada junto con Wallace, que llegó a las mismas conclusiones independientemente, es que pequeños cambios heredables en los seres vivos y la selección son los dos hechos que provocan el cambio en la Naturaleza y la generación de nuevas especies. Pero Darwin desconocía cual es la base de la herencia, pensaba que los rasgos de un ser vivo eran como un fluido, y que los "fluidos" de los dos padres se mezclaban en la descendencia; esta hipótesis tenía el problema de que al cabo de cierto tiempo, una población tendría los mismos rasgos intermedios.
Fue Mendel quien descubrió que los caracteres se heredaban de forma discreta, y que se tomaban del padre o de la madre, dependiendo de su carácter dominante o recesivo. A estos caracteres que podían tomar diferentes valores se les llamaron genes, y a los valores que podían tomar, alelos. En realidad, las teorías de Mendel, que trabajó en total aislamiento, se olvidaron y no se volvieron a redescubrir hasta principios del siglo XX. Además, hasta 1930 el geneticista inglés Robert Aylmer no relacionó ambas teorías, demostrando que los genes mendelianos eran los que proporcionaban el mecanismo necesario para la evolución.
Más o menos por la misma época, el biólogo alemán Walther Flemming describió los cromosomas, como ciertos filamentos en los que se agregaba la cromatina del núcleo celular durante la división; poco más adelante se descubrió que las células de cada especie viviente tenían un número fíjo y característico de cromosomas.
Y no fue hasta los años 50, cuando Watson y Crick descubrieron que la base molecular de los genes está en el ADN, ácido desoxirribonucleico. Los cromosomas están compuestos de ADN, y por tanto los genes están en los cromosomas.La macromolécula de ADN está compuesta por bases púricas y pirimidínicas, la adenina, citosina, guanina y timina. La combinación y la secuencia de estas bases forma el código genético, único para cada ser vivo. Grupos de 3 bases forman un codon, y cada codon codifica un aminoácido (el que exprese ese aminoácido o no depende de otros factores); el código genético codifica todas las proteinas que forman parte de un ser vivo. Mientras que al código genético se le llama genotipo, al cuerpo que construyen esas proteínas, modificado por la presión ambiental, la historia vital, y otros mecanismos dentro del cromosoma, se llama fenotipo.
Proyectos como el del Genoma Humano tratan de identificar cuáles son estos genes, sus posiciones, y sus posibles alteraciones, que habitualmente conducen a enfermedades.
Todos estos hechos forman hoy en día la teoría del neo-darwinismo, que afirma que la historia de la mayoría de la vida está causada por una serie de procesos que actúan en y dentro de las poblaciones: reproducción, mutación, competición y selección.
La evolución se puede definir entonces como cambios en el pool o conjunto genético de una población.
Un tema polémico, con opiniones variadas dependiendo de si se trata de informáticos evolutivos o de biólogos o geneticistas, es si la evolución optimiza o no.
Según los informáticos evolutivos, la evolución optimiza, puesto que va creando seres cada vez más perfectos, cuya cumbre es el hombre; además, indicios de esta optimización se encuentran en el organismo de los animales, desde el tamaño y tasa de ramificación de las arterias, diseñada para maximizar flujo, hasta el metabolismo, que optimiza la cantidad de energía extraída de los alimentos.
Sin embargo, los geneticistas y biólogos evolutivos afirman que la evolución no optimiza, sino que adapta y optimiza localmente en el espacio y el tiempo; evolución no significa progreso. Un organismo más evolucionado puede estar en desventaja competitiva con uno de sus antepasados, si se colocan en el ambiente del último.
2.1 Mecanismos de cambio en la evolución
Estos mecanismos de cambio serán necesarios para entender los algoritmos evolutivos, pues se trata de imitarlos para resolver problemas de ingeniería; por eso merece la pena conocerlos en más profundidad. Los mecanismos de cambio alteran la proporción de alelos de un tipo determinado en una población, y se dividen en dos tipos: los que disminuyen la variabilidad, y los que la aumentan.
Los principales mecanismos que disminuyen la variabilidad son los siguientes:
-
Selección natural:
Los individuos que tengan algún rasgo que los haga menos válidos para realizar su tarea de seres vivos, no llegarán a reproducirse, y, por tanto, su patrimonio genético desaparecerá del pool; algunos no llegarán ni siquiera a nacer. Esta selección sucede a muchos niveles: competición entre miembros de la especie (intraespecífica), competición entre diferentes especies, y competición predador-presa, por ejemplo. También es importante la selección sexual, en la cual las hembras eligen el mejor individuo de su especie disponible para reproducirse.
-
Deriva génica:
El simple hecho de que un alelo sea más común en la población que otro, causará que la proporción de alelos de esa población vaya aumentando en una población aislada, lo cual a veces da lugar a fenómenos de especiación, por ejemplo, por el denominado efecto fundador.
Otros mecanismos aumentan la diversidad, y suceden generalmente en el ámbito molecular. Los más importantes son:
-
Mutación:
La mutación es una alteración del código genético, que puede suceder por múltiples razones. En muchos casos, las mutaciones las elimina la ADN-polimerasa, la navaja del ejército suizo del ADN, que igual duplica, que corrige, que desinvierte un cacho genético mal colocado. En muchos otros casos, las mutaciones, que cambian un nucleótido por otro, son letales, y los individuos ni siquiera llegan a desarrollarse, pero a veces se da lugar a la producción de una proteína que aumenta la supervivencia del individuo, y que, por tanto, es pasada a la descendencia. Las mutaciones son totalmente aleatorias, y son el mecanismo básico de generación de variedad genética. A pesar de lo que se piensa habitualmente, la mayoría de las mutaciones ocurren de forma natural, aunque existen sustancias mutagénicas que aumentan su frecuencia.
-
Poliploidía:
Mientras que las células normales poseen dos copias de cada cromosoma, y las células reproductivas una (haploides), puede suceder por accidente que alguna célula reproductiva tenga dos copias; si se logra combinar con otra célula diploide o haploide dará lugar a un ser vivo con varias copias de cada cromosoma. La mayoría de las veces, la poliploidía da lugar a individuos con algún defecto (por ejemplo, el tener 3 copias del cromosoma 21 da lugar al mongolismo), pero en algunos casos se crean individuos viables. Un caso de mutación fue el que sufrió (o disfrutó) el mosquito Culex pipiens, en el cual se duplicó un gen que generaba una enzima que rompía los organofosfatos, componentes habituales de los insecticidas;
-
Recombinación:
Cuando las dos células sexuales, o gametos, una masculina y otra femenina se combinan, los cromosomas de cada una también lo hacen, intercambiándose genes, que a partir de ese momento pertenecerán a un cromosoma diferente. A veces también se produce traslocación dentro de un cromosoma; una secuencia de código se elimina de un sitio y aparece en otro sitio del cromosoma, o en otro cromosoma.
-
Flujo genético:
O intercambio de material genético entre seres vivos de diferentes especies. Normalmente se produce a través de un vector, que suelen ser virus o bacterias; estas incorporan a su material genético genes procedentes de una especie a la que han infectado, y cuando infectan a un individuo de otra especie pueden transmitirle esos genes a los tejidos generativos de gametos.
En resumen, la selección natural actúa sobre el fenotipo y suele disminuir la diversidad, haciendo que sobrevivan solo los individuos más aptos (aunque esta frase, bien mirada, es una redundancia: ¿Sobreviven los mejores o son los mejores porque sobreviven?); los mecanismos que generan diversidad y que combinan características actúan habitualmente sobre el genotipo.
3 Algoritmo genético simple.
3.1 Introducción
John Holland desde pequeño, se preguntaba cómo logra la naturaleza, crear seres cada vez más perfectos. No sabía la respuesta, pero tenía una cierta idea de como hallarla: tratando de hacer pequeños modelos de la naturaleza, que tuvieran alguna de sus características, y ver cómo funcionaban, para luego extrapolar sus conclusiones a la totalidad.
Fue a principios de los 60, en la Universidad de Michigan en Ann Arbor, donde, dentro del grupo Logic of Computers, sus ideas comenzaron a desarrollarse y a dar frutos. Y fue, además, leyendo un libro escrito por un biólogo evolucionista, R. A. Fisher, titulado La teoría genética de la selección natural, como comenzó a descubrir los medios de llevar a cabo sus propósitos de comprensión de la naturaleza. De ese libro aprendió que la evolución era una forma de adaptación más potente que el simple aprendizaje, y tomó la decisión de aplicar estas ideas para desarrollar programas bien adaptados para un fin determinado.
En esa universidad, Holland impartía un curso titulado Teoría de sistemas adaptativos. Dentro de este curso, y con una participación activa por parte de sus estudiantes, fue donde se crearon las ideas que más tarde se convertirían en los algoritmos genéticos.
Por tanto, cuando Holland se enfrentó a los algoritmos genéticos, los objetivos de su investigación fueron dos:
-
imitar los procesos adaptativos de los sistemas naturales, y
-
diseñar sistemas artificiales (normalmente programas) que retengan los mecanismos importantes de los sistemas naturales.
Unos 15 años más adelante, David Goldberg, actual delfín de los algoritmos genéticos, conoció a Holland, y se convirtió en su estudiante. Goldberg era un ingeniero industrial trabajando en diseño de pipelines, y fue uno de los primeros que trató de aplicar los algoritmos genéticos a problemas industriales. Aunque Holland trató de disuadirle, porque pensaba que el problema era excesivamente complicado como para aplicarle algoritmos genéticos, Goldberg consiguió lo que quería, escribiendo un algoritmo genético en un ordenador personal Apple II. Estas y otras aplicaciones creadas por estudiantes de Holland convirtieron a los algoritmos genéticos en un campo con base suficiente aceptado para celebrar la primera conferencia en 1985, ICGA´85.
3.2 Anatomía de un algoritmo genético simple
Los algoritmos genéticos son métodos sistemáticos para la resolución de problemas de búsqueda y optimización que aplican a estos los mismos métodos de la evolución biológica: selección basada en la población, reproducción sexual y mutación.
Los algoritmos genéticos son métodos de optimización, que tratan de resolver el mismo conjunto de problemas que se ha contemplado anteriormente, es decir, el objetivo es hallar (xi,...,xn) tales que F(xi,...,xn) sea máximo.
En un algoritmo genético, tras parametrizar el problema en una serie de variables, (xi,...,xn) se codifican en un cromosoma.
Todos los operadores utilizados por un algoritmo genético se aplicarán sobre estos cromosomas, o sobre poblaciones de ellos. En el algoritmo genético va implícito el método para resolver el problema; son sólo parámetros de tal método los que están codificados, a diferencia de otros algoritmos evolutivos como la programación genética.
Hay que tener en cuenta que un algoritmo genético es independiente del problema, lo cual lo hace un algoritmo robusto, por ser útil para cualquier problema, pero a la vez débil, pues no está especializado en ninguno.
Las soluciones codificadas en un cromosoma compiten para ver cuál constituye la mejor solución (aunque no necesariamente la mejor de todas las soluciones posibles).
El ambiente, constituido por las otras camaradas soluciones, ejercerá una presión selectiva sobre la población, de forma que sólo los mejor adaptados (aquellos que resuelvan mejor el problema) sobrevivan o leguen su material genético a las siguientes generaciones, igual que en la evolución de las especies.
La diversidad genética se introduce mediante mutaciones y reproducción sexual.
En la Naturaleza lo único que hay que optimizar es la supervivencia, y eso significa a su vez maximizar diversos factores y minimizar otros. Un algoritmo genético, sin embargo, se usará habitualmente para optimizar sólo una función, no diversas funciones relacionadas entre sí simultáneamente. Este tipo de optimización, denominada optimización multimodal, también se suele abordar con un algoritmo genético especializado.
Por lo tanto:
3.3 Codificación de las variables
Los algoritmos genéticos requieren que el conjunto se codifique en un cromosoma. Cada cromosoma tiene varios genes, que corresponden a sendos parámetros del problema. Para poder trabajar con estos genes en el ordenador, es necesario codificarlos en una cadena, es decir, una ristra de símbolos (números o letras) que generalmente va a estar compuesta de 0s y 1s.
EJEMPLO 1:
Si un atributo (tiempo) puede tomar tres valores posibles (despejado, nublado, lluvioso) una manera de representarlo es mediante tres bits de forma que:
(Tiempo = Nublado ó Lluvioso) y (Viento = Fuerte) se representaría con la siguiente cadena: 011 10.
De esta forma podemos representar fácilmente conjunciones de varios atributos para expresar restricciones (precondiciones) mediante la concatenación de dichas cadenas de bits.
Además si tenemos otro atributo “Viento” que puede ser Fuerte o Moderado,se representaría con la siguiente cadena: 011 10.
Las postcondiciones de las reglas se pueden representar de la misma forma. Por ello una regla se puede describir como la concatenación de la precondición y la postcondición.
Ejemplo2:
“JugaralTenis” puede ser Cierto o Falso.
Si Viento = Fuerte entonces JugaralTenis = Cierto se representaría mediante la cadena 111 10 10. Donde los tres primeros bits a uno indican que el atributo “Tiempo” no afecta a nuestra regla.
Cabe destacar que una regla del tipo 111 10 11 no tiene demasiado sentido, puesto que no impone restricciones en la postcondición. Para solucionar esto, una alternativa es codificar la postcondición con un único bit (1 = Cierto y 0 = Falso). Otra opción es condicionar los operadores genéticos para que no produzcan este tipo de cadenas o conseguir que estas hipótesis tengan una adecuación muy baja (según la función de evaluación) para que no logren pasar a la próxima generación de hipótesis.
A continuación se comienza con una población de soluciones posibles, que pueden ser generadas al azar o mediante algún método que produzca soluciones relativamente satisfactorias. A partir de este punto inicial, el algoritmo procede por etapas que ejecutan los pasos elementales siguientes:
Se evalúan todas las soluciones de la población, con el fin de otorgar más probabilidades de emparejamiento a las más satisfactorias.
Mediante un mecanismo de azar, aunque dando más oportunidades a las mejor evaluadas, se eligen las soluciones que han de cruzarse entre sí para dar lugar a descendencia.
El cruce opera sobre las cadenas de los genotipos de cada pareja de las soluciones elegidas como progenitores. El sistema mediante el cual se obtienen nuevas soluciones a partir las precedentes, es decir lo que se llama el operador de cruzamiento, puede ser distinto según las técnicas específicas empleadas. El que se describe en el punto siguiente es uno de los más generalizados.
3.4 Algoritmo genético propiamente dicho
Para comenzar la competición, se generan aleatoriamente una serie de cromosomas. El algoritmo genético procede de la forma siguiente:
Cada uno de los pasos consiste en una actuación sobre las cadenas de bits, es decir, la aplicación de un operador a una cadena binaria. Se les denominan, por razones obvias, operadores genéticos, y hay tres principales: selección, crossover o recombinación y mutación; aparte de otros operadores genéticos no tan comunes, todos ellos se verán a continuación.
Un algoritmo genético tiene también una serie de parámetros que se tienen que fijar para cada ejecución, como los siguientes:
Tamaño de la población:
debe de ser suficiente para garantizar la diversidad de las soluciones, y, además, tiene que crecer más o menos con el número de bits del cromosoma, aunque nadie ha aclarado cómo tiene que hacerlo. Por supuesto, depende también del ordenador en el que se esté ejecutando.
Condición de terminación:
lo más habitual es que la condición de terminación sea la convergencia del algoritmo genético o un número prefijado de generaciones.
3.5 Evaluación y selección
Durante la evaluación, se decodifica el gen, convirtiéndose en una serie de parámetros de un problema, se halla la solución del problema a partir de esos parámetros, y se le da una puntuación a esa solución en función de lo cerca que esté de la mejor solución. A esta puntuación se le llama fitness.
Por ejemplo, supongamos que queremos hallar el máximo de la función f(x), una parábola invertida con el máximo en x=1. En este caso, el único parámetro del problema es la variable x. La optimización consiste en hallar un x tal que F(x) sea máximo. Crearemos, pues, una población de cromosomas, cada uno de los cuales contiene una codificación binaria del parámetro x. Lo haremos de la forma siguiente: cada byte, cuyo valor está comprendido entre 0 y 255, se transformará para ajustarse al intervalo [-1,1], donde queremos hallar el máximo de la función.
| Valor binario | Decodificación | Evaluación f(x) |
| 10010100 | 21 | 0,9559 |
| 10010001 | 19 | 0,9639 |
| 101001 | -86 | 0,2604 |
| 1000101 | -58 | 0,6636 |
El fitness determina siempre los cromosomas que se van a reproducir, y aquellos que se van a eliminar, pero hay varias formas de considerarlo para seleccionar la población de la siguiente generación:
Usar el orden, o rango, y hacer depender la probabilidad de permanencia o evaluación de la posición en el orden.
-
Aplicar una operación al fitness para escalarlo; como por ejemplo el escalado sigma. En este esquema el fitness se escala
-
En algunos casos, el fitness no es una sola cantidad, sino diversos números, que tienen diferente consideración. Basta con que tal fitness forme un orden parcial, es decir, que se puedan comparar dos individuos y decir cuál de ellos es mejor. Esto suele suceder cuando se necesitan optimizar varios objetivos.
Una vez evaluado el fitness, se tiene que crear la nueva población teniendo en cuenta que los buenos rasgos de los mejores se transmitan a ésta. Para ello, hay que seleccionar a una serie de individuos encargados de tan ardua tarea. Y esta selección, y la consiguiente reproducción, se puede hacer de dos formas principales:
Basado en el rango:
En este esquema se mantiene un porcentaje de la población, generalmente la mayoría, para la siguiente generación. Se coloca toda la población por orden de fitness, y los M menos dignos son eliminados y sustituidos por la descendencia de alguno de los M mejores con algún otro individuo de la población.
A este esquema se le pueden aplicar otros criterios; por ejemplo, se crea la descendencia de uno de los paladines/amazonas, y esta sustituye al más parecido entre los perdedores. Esto se denomina crowding, y fue introducido por DeJong.
Una variante de este es el muestreado estocástico universal, que trata de evitar que los individuos con más fitness copen la población dando más posibilidades al resto de la población; de esta forma, la distribución estadística de descendientes en la nueva población es más parecida a la real.
Rueda de ruleta:
se crea un conjunto genético formado por cromosomas de la generación actual, en una cantidad proporcional a su fitness. Si la proporción hace que un individuo domine la población, se le aplica alguna operación de escalado. Dentro de este conjunto, se cogen parejas aleatorias de cromosomas y se emparejan, sin importar incluso que sean del mismo progenitor (para eso están otros operadores, como la mutación). Hay otras variantes: por ejemplo, en la nueva generación se puede incluir el mejor representante de la generación actual. En este caso, se denomina método elitista.
Selección de torneo:
se escogen aleatoriamente un número T de individuos de la población, y el que tiene puntuación mayor se reproduce, sustituyendo su descendencia al que tiene menor puntuación.
3.6 Crossover
Consiste en el intercambio de material genético entre dos cromosomas (a veces más, como el operador orgía propuesto por Eiben et al.). El crossover es el principal operador genético, hasta el punto que se puede decir que no es un algoritmo genético si no tiene crossover, y, sin embargo, puede serlo perfectamente sin mutación, según descubrió Holland. El teorema de los esquemas confía en él para hallar la mejor solución a un problema, combinando soluciones parciales.
Para aplicar el crossover, entrecruzamiento o recombinación, se escogen aleatoriamente dos miembros de la población. No pasa nada si se emparejan dos descendiente de los mismos padres; ello garantiza la perpetuación de un individuo con buena puntuación (y, además, algo parecido ocurre en la realidad; es una práctica utilizada, por ejemplo, en la cría de ganado, llamada inbreeding, y destinada a potenciar ciertas características frente a otras). Sin embargo, si esto sucede demasiado a menudo, puede crear problemas: toda la población puede aparecer dominada por los descendientes de algún gen, que, además, puede tener caracteres no deseados. Esto se suele denominar en otros métodos de optimización atranque en un mínimo local, y es uno de los principales problemas con los que se enfrentan los que aplican algoritmos genéticos.
En cuanto al teorema de los esquemas, se basa en la noción de bloques de construcción. Una buena solución a un problema está constituida por unos buenos bloques, igual que una buena máquina está hecha por buenas piezas. El crossover es el encargado de mezclar bloques buenos que se encuentren en los diversos progenitores, y que serán los que den a los mismos una buena puntuación. La presión selectiva se encarga de que sólo los buenos bloques se perpetúen, y poco a poco vayan formando una buena solución. El teorema de los esquemas viene a decir que la cantidad de buenos bloques se va incrementando con el tiempo de ejecución de un algoritmo genético, y es el resultado teórico más importante en algoritmos genéticos.
El intercambio genético se puede llevar a cabo de muchas formas, pero hay dos grupos principales
Crossover n-puntos:
Los dos cromosomas se cortan por n puntos, y el material genético situado entre ellos se intercambia. Lo más habitual es un crossover de un punto o de dos puntos.
Padre
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Madre
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Hijo
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
Crossover uniforme:
Se genera un patrón aleatorio de 1s y 0s, y se intercambian los bits de los dos cromosomas que coincidan donde hay un 1 en el patrón. O bien se genera un número aleatorio para cada bit, y si supera una determinada probabilidad se intercambia ese bit entre los dos cromosomas.
Padre
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Madre
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Hijo
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Crossover especializados:
En algunos problemas, aplicar aleatoriamente el crossover da lugar a cromosomas que codifican soluciones inválidas; en este caso hay que aplicar el crossover de forma que genere siempre soluciones válidas. Un ejemplo de estos son los operadores de crossover usados en el problema del viajante.
3.7 Mutación
En la Evolución, una mutación es un suceso bastante poco común (sucede aproximadamente una de cada mil replicaciones), como ya se ha visto anteriormente. En la mayoría de los casos las mutaciones son letales, pero en promedio, contribuyen a la diversidad genética de la especie. En un algoritmo genético tendrán el mismo papel, y la misma frecuencia (es decir, muy baja).
Una vez establecida la frecuencia de mutación, por ejemplo, uno por mil, se examina cada bit de cada cadena cuando se vaya a crear la nueva criatura a partir de sus padres (normalmente se hace de forma simultánea al crossover). Si un número generado aleatoriamente está por debajo de esa probabilidad, se cambiará el bit (es decir, de 0 a 1 o de 1 a 0). Si no, se dejará como está. Dependiendo del número de individuos que haya y del número de bits por individuo, puede resultar que las mutaciones sean extremadamente raras en una sola generación.
No hace falta decir que no conviene abusar de la mutación. Es cierto que es un mecanismo generador de diversidad, y, por tanto, la solución cuando un algoritmo genético está estancado, pero también es cierto que reduce el algoritmo genético a una búsqueda aleatoria. Siempre es más conveniente usar otros mecanismos de generación de diversidad, como aumentar el tamaño de la población, o garantizar la aleatoriedad de la población inicial.
Este operador, junto con la anterior y el método de selección de ruleta, constituyen un algoritmo genético simple, sga, introducido por Goldberg en su libro.
3.8 Otros operadores
No se usan en todos los problemas, sino sólo en algunos, y en principio su variedad es infinita. Generalmente son operadores que exploran el espacio de soluciones de una forma más ordenada, y que actúan más en las últimas fases de la búsqueda, en la cuál se pasa de soluciones "casi buenas" a "buenas" soluciones.
3.8.1 Cromosomas de longitud variable
Hasta ahora se han descrito cromosomas de longitud fija, donde se conoce de antemano el número de parámetros de un problema. Pero hay problemas en los que esto no sucede. Por ejemplo, en un problema de clasificación, donde dado un vector de entrada, queremos agruparlo en una serie de clases, podemos no saber siquiera cuántas clases hay. O en diseño de redes neuronales, puede que no se sepa (de hecho, nunca se sabe) cuántas neuronas se van a necesitar. Por ejemplo, en un perceptrón hay reglas que dicen cuantas neuronas se deben de utilizar en la capa oculta; pero en un problema determinado puede que no haya ninguna regla heurística aplicable; tendremos que utilizar los algoritmos genéticos para hallar el número óptimo de neuronas.
En estos casos, necesitamos dos operadores más: añadir y eliminar. Estos operadores se utilizan para añadir un gen, o eliminar un gen del cromosoma. La forma más habitual de añadir un locus es duplicar uno ya existente, el cuál sufre mutación y se añade al lado del anterior. En este caso, los operadores del algoritmo genético simple (selección, mutación, crossover) funcionarán de la forma habitual, salvo, claro está, que sólo se hará crossover en la zona del cromosoma de menor longitud.
3.8.2 Operadores de nicho (ecológico)
Otros operadores importantes son los operadores de nicho. Estos operadores están encaminados a mantener la diversidad genética de la población, de forma que cromosomas similares sustituyan sólo a cromosomas similares, y son especialmente útiles en problemas con muchas soluciones; un algoritmo genético con estos operadores es capaz de hallar todos los máximos, dedicándose cada especie a un máximo. Más que operadores genéticos, son formas de enfocar la selección y la evaluación de la población.
Uno de las formas de llevar esto a cabo ya ha sido nombrada, la introducción del crowding (apiñamiento). Otra forma es introducir una función de compartición o sharing, que indica cuán similar es un cromosoma al resto de la población. La puntuación de cada individuo se dividirá por esta función de compartición, de forma que se facilita la diversidad genética y la aparición de individuos diferentes.
También se pueden restringir los emparejamientos, por ejemplo, a aquellos cromosomas que sean similares. Para evitar las malas consecuencias del inbreeding (destinado a potenciar ciertas características frente a otras) que suele aparecer en poblaciones pequeñas, estos periodos se intercalan con otros periodos en los cuáles el emparejamiento es libre.
3.8.3 Operadores especializados
En una serie de problemas hay que restringir las nuevas soluciones generadas por los operadores genéticos, pues no todas las soluciones generadas van a ser válidas, sobre todo en los problemas con restricciones. Por ello, se aplican operadores que mantengan la estructura del problema. Otros operadores son simplemente generadores de diversidad, pero la generan de una forma determinada:
Zap:
En vez de cambiar un solo bit de un cromosoma, cambia un gen completo de un cromosoma.
Creep:
Este operador aumenta o disminuye en 1 el valor de un gen; sirve para cambiar suavemente y de forma controlada los valores de los genes.
Transposición:
Similar al crossover y a la recombinación genética, pero dentro de un solo cromosoma; dos genes intercambian sus valores, sin afectar al resto del cromosoma. Similar a este es el operador de eliminación-reinserción, en el que un gen cambia de posición con respecto a los demás.
3.8.4 Aplicando operadores genéticos
En toda ejecución de un algoritmo genético hay que decidir con qué frecuencia se va a aplicar cada uno de los algoritmos genéticos; en algunos casos, como en la mutación o el crossover uniforme, se debe de añadir algún parámetro adicional, que indique con qué frecuencia se va a aplicar dentro de cada gen del cromosoma. La frecuencia de aplicación de cada operador estará en función del problema; teniendo en cuenta los efectos de cada operador, tendrá que aplicarse con cierta frecuencia o no. Generalmente, la mutación y otros operadores que generen diversidad se suele aplicar con poca frecuencia; la recombinación se suele aplicar con frecuencia alta.
En general, la frecuencia de los operadores no varía durante la ejecución del algoritmo, pero hay que tener en cuenta que cada operador es más efectivo en un momento de la ejecución. Por ejemplo, al principio, en la fase denominada de exploración, los más eficaces son la mutación y la recombinación; posteriormente, cuando la población ha convergido en parte, la recombinación no es útil, pues se está trabajando con individuos bastante similares, y es poca la información que se intercambia. Sin embargo, si se produce un estancamiento, la mutación tampoco es útil, pues está reduciendo el algoritmo genético a una búsqueda aleatoria; y hay que aplicar otros operadores. En todo caso, se pueden usar operadores especializados.
Por ejemplo, en el algoritmo genético para jugar al MasterMind, se usan varios operadores genéticos: transposición, mutación y entrecruzamiento. Sin embargo, la mutación y el crossover dejan de ser efectivos en el momento que la combinación que se ha jugado tiene los colores correctos, y en cualquier caso la tasa de mutación tendrá que ser mayor cuantos menos colores haya averiguados; por eso las tasas varían durante la ejecución, convirtiéndose eventualmente en 0.
EJEMPLO SIMPLE DE ALGORITMOS GENÉTICO:
Supongamos que hemos de calcular el máximo de una función f(x) en un intervalo [a,b]. Pues bien, sencillo, derivamos e igualamos a cero, ¿no?. Pues no. Se me olvidaba decir que no conocemos f(x), aunque sí podemos calcular o estimar su valor en cualquier punto.
He aquí los pasos a seguir:
-
Estimamos con qué resolución queremos trabajar. Es decir, elegimos el número de puntos que vamos a examinar dentro de ese intervalo. Si, por ejemplo, el intervalo es el [0,100] y ponemos una resolución de 0.5, pues tendremos 200 puntos en el intervalo.
-
Generamos una población inicial de n individuos; que serán -no podía ser menos- n números (elegidos al azar). Es decir, ya tenemos x1, x2, ... ,xn. Todos ellos, entre a y b, los límites de nuestro intervalo.
-
Ahora hemos de dar mayor capacidad de reproducción a los mejor dotados. Si estamos buscando el máximo, pues el mejor dotado será aquel cuyo valor de f(xi) sea mayor. Hasta aquí, todo de lo más normal.
Pues de los n individuos que tenemos, vamos a crear una población intermedia, que será los que se van a recombinar. Calculamos la frecuencia de cada uno de los n genotipos en la primera población .
Bueno, tenemos que calcular esas probabilidades: p(xi)=f(xi)/suma_total. Les he llamado probabilidades, aunque en realidad son frecuencias, por aquello de no confundir la notación. Siguiendo con esta tónica, definimos P(xi) como la función de distribución: P(xj) es la suma, desde cero hasta j, de los p(xi).
Creo que es necesario un breve ejemplo para aclarar las cosas (aunque también está el mail). Supongamos que nuestro n sea igual a 4, y que, por ejemplo, tenemos:
f(x0)=10
f(x1)=40
f(x2)=30
f(x3)=20
Por lo tanto,
p(x0)=0.1
p(x1)=0.4
p(x2)=0.3
p(x3)=0.2
y también
P(x0)=0.1
P(x1)=0.5
P(x2)=0.8
P(x3)=1.0
Esta claro que los p(xi) suman 1. A continuación generamos n números aleatorios entre 0 y 1. Cada uno de esos números -por ejemplo, t- estará relacionado con un individuo de nuestra generación intermedia; de la siguiente forma:
si t está entre P(xi) y P(xi+1) escogemos xi+1)
Seguimos con el ejemplo: Si nuestros cuatro números aleatorios son 0.359, 0.188, 0.654 y 0.399, entonces nuestra generación intermedia será:
| Número aleatorio | Individuo seleccionado | Nuevo valor |
| 0.1<0.359<0.5 | x1 | x0 |
| 0.1<0.188<0.5 | x1 | x1 |
| 0.5<0.654<0.8 | x2 | x2 |
| 0.1<0.399<0.5 | x1 | x3 |
Como se ve, está claro que, pese al azar el individuo mejor dotado es el más favorecido.
-
El siguiente paso es la recombinación. Se puede hacer de la forma que nos parezca más adecuada. En primer lugar hay que buscar las parejas. Se trata de obtener una nueva generación como mezcla de esta con la que estamos trabajando. Una vez que tenemos las parejas, hemos de hacer la recombinación. Una alternativa: media aritmética;(1) otra: media geométrica(2). Otra, la más usada: cortar los dos números "papás" por un lugar al azar (3) y conseguir los "hijos" intercambiando partes. Por si este último punto no ha quedado demasiado claro, digamos que, si los individuos son 456 y 123, elegimos al azar un número entre 1 y 2 (ya que hay tres cifras). Si, por ejemplo, nos sale el 1, pues un posible hijo podría ser el 4-23 y otro 1-56. Aunque hay que decir que lo más habitual es trabajar en base 2 (al menos, los números serán más largos).
-
En este momento ya tenemos una nueva generación. Generalmente, mejor dotada que la inicial. Lo que se hace ahora es volver al tercer punto (cálculo de una población intermedia). Por supuesto, el algoritmo se para cuando queramos. Por ejemplo, cuando llevemos un número de iteraciones determinado, o cuando la población no mejore demasiado.
-
Una variante posible es permitir la existencia de mutaciones (por ejemplo, introducir cada cierto número de generaciones alguna variación en una cifra en busca de mejores soluciones. Esto es interesante debido a que, por ejemplo, si estamos dando vueltas en torno a un máximo local, la variación introducida podría llevarnos hacia un genotipo mejor dotado.
-
Otra variante es la elitista, consistente en que los mejores genotipos no se recombinen, sino que pasen directamente -tal cual- a la siguiente generación.
ejemplo completo de un algoritmo genético
La finalidad de este ejemplo es construir un planeador de rutas, capaz de encontrar la ruta más corta a la salida más cercana, para cada una de las “n” personas que se encuentran en un cuarto.
Este cuarto contiene obstáculos estáticos y varias salidas. La ruta encontrada para la persona “x” no debe llevarla a chocar con algún obstáculo ni con otra persona que a su vez se está moviendo en el cuarto.

La interface del programa tiene la siguiente simbología:
Cubos de colores y mas pequeños : Personas
Cubos azules: Obstáculos
Cuadros rojos: Salidas
Los pasos de un algoritmo genético son los siguientes:
1.- Inicialización:
En este primer paso se crea aleatoriamente un conjunto de individuos (que están sobre el espacio S).
Inicialmente tenemos 20 individuos. Los individuos se representan como un vector, cuyos valores van del 0-7, y que significan lo siguiente:
0 -> Camina un paso a la izquierda
1 -> Camina un paso a la derecha
2 -> Camina un paso adelante
3 -> Camina un paso atrás
-> Camina en diagonal izquierda hacia arriba
-> Camina en diagonal izquierda hacia abajo
-> Camina en diagonal derecha hacia abajo
-> Camina en diagonal derecha hacia arriba
8 -> Quédate en tu lugar
Éstos serían dos ejemplos de individuos:
1) 2 - 1 - 2 - 0 - 7 - 4 - 3 - 6 - 3 - 3 - 3 - 0 - 5 - 0 - 3 - 3 - 3 - 1 - 1 - 1 - 3 - 5 - 1 - 4 - 7 - 4 - 3 - 1 - 6 - 1 - 2 -
2) 0 - 4 - 1 - 7 - 5 - 3 - 1 - 1 - 3 - 3 - 3 - 7 - 5 - 1 - 2 - 5 - 6 - 4 -
Después el algoritmo itera en los siguientes pasos hasta que se cumpla alguna condición.
En este caso dicha condición es que evolucionen 6 generaciones.
2.- Evaluación:
La Función F es computada para cada individuo, ordenando la población del mejor individuo al peor. En el ejemplo, la función a optimizar es la longitud de los individuos. Es decir deseamos obtener un individuo con longitud mínima. Por ello, se ordenan en base a su longitud y en orden ascendente.
3.- Selección:
Se selecciona con la regla de selección - explicada a continuación - una pareja de individuos. La regla utilizada es roulette wheel selection, que elige en base a probabilidad proporcional a su calificación:
1.- Se genera un número aleatorio r E [0,1].
2.- Se multiplica r por la suma de las calificaciones de la población (S), obteniéndose c = rS.
3.- Se establece la calificación acumulada (Ca) y el índice en cero: Ca = 0, i=0
4.- A la calificación acumulada se le suma la calificación del i-ésimo individuo:
Ca = Ca + calif(i)
5.- Si Ca > c entonces el i-esimo individuo es seleccionado.
6.- Si no, entonces se incrementa i y se regresa al paso 4.
Esta selección es con reemplazo, es decir, un mismo individuo puede ser seleccionado varias veces. Así que cada vez que se selecciona un individuo no se quita de la población de la que se está seleccionando, permanece en ella para que pueda ser elegido nuevamente.
4.- Reproducción:
Se generan nuevos individuos a partir de la pareja seleccionada en el paso 3.
El algoritmo de reproducción que se ha utilizado es el siguiente:
! Una vez seleccionados 2 individuos p1 y p2 (llamados padres) se procede a cruzarlos.
! Generamos un número aleatorio entre 1 y (longitud de p1)/2, llamado n1.
! Generamos un número aleatorio entre (longitud de p2)/2 y longitud de p2, llamado n2.
! Calculamos la posición en la que se encuentra p1 al dar n1 pasos, y la llamamos pasosp1.
! Calculamos la posición en la que se encuentra p2 al dar (longitud de p2)/2 pasos, y la llamamos pasosp2.
! Generamos un camino aleatorio de pasosp1 a pasosp2, llamado camino_intermedio. Este camino aleatorio verifica que no choque con ningún obstáculo predefinido (estático).
! Copiamos los primeros n1 pasos de p1 en el nuevo individuo ni1.
! Copiamos camino_intermedio a ni1.
-
Copiamos los pasos de p2 de n2 a longitud p2.
Y de la misma manera generamos el segundo nuevo individuo, sólo que ahora tomamos el inicio de p2 y el final de p1.
Esta cruza nos garantiza que obtengamos individuos válidos, es decir que nos van a dar un camino que inicie en la posición original de la persona y finalice en alguna salida. Y que además no choque con ningún obstáculo.
Después de repetir 6 veces los pasos del 2 al 4, se obtiene una población final.
El algoritmo además de estos pasos, incorpora un quinto paso al que llamamos entrenamiento.
5.- Entrenamiento:
Repite los pasos del 1 al 4 n veces. El primer algoritmo genético coloca en la población inicial del segundo algoritmo genético, a su mejor individuo (lo coloca 2 veces, para asegurarse de que va a preservarse en las siguientes generaciones), el segundo hace lo mismo con el tercero, y así sucesivamente hasta n.
Los algoritmos genéticos tienen una característica peculiar, que es que cada vez que se ejecuta nos da (muy probablemente) respuestas diferentes, y esto es porque la población inicial se genera aleatoriamente.
Estos entrenamientos nos permiten tomar el mejor individuo evolucionado del algoritmo genético anterior, y a su vez generar nuevos individuos. Esto es conocido también como elitismo. Con esto generamos n veces poblaciones aleatorias y (n-1) veces la población inicial al menos tiene un buen individuo. Este nuevo individuo al cruzarlo con algún otro buen individuo generado aleatoriamente puede ser que nos dé uno aún mejor.
Parámetros que deben ser especificados en el programa:
Nº de generaciones: cantidad de veces que se produce una nueva generación de individuos, utilizando las reglas anteriormente explicadas. Por lógica, cuantas más generaciones produzcamos, obtendremos mejores individuos.
Nº de individuos por generación: en este ejemplo, la cantidad de individuos de una generación a otra es constante, no varía.
Nº de entrenamientos: cantidad de veces que se lleva a cabo un entrenamiento entre diferentes generaciones de individuos.![]()
![]()
CONCLUSIÓN DEL TRABAJO:
Como hemos podido observar, la principal ventaja de los algoritmos genéticos radica en su sencillez. Se requiere poca información sobre el espacio de búsqueda ya que se trabaja sobre un conjunto de soluciones o parámetros codificados (hipótesis o individuos). Se busca una solución por aproximación de la población, en lugar de una aproximación punto a punto. Con un control adecuado podemos mejorar la aptitud promedio de la población, obteniendo nuevos y mejores individuos y, por lo tanto, mejores soluciones.
Se consigue un equilibrio entre la eficacia y la eficiencia. Este equilibrio es configurable mediante los parámetros y operaciones usados en el algoritmo. Así, por ejemplo, bajando el valor del umbral conseguiremos una rápida solución a cambio de perder en “calidad”. Si aumentamos dicho valor, tendremos una mejor solución a cambio de un mayor tiempo consumido en la búsqueda. Es decir, obtenemos una buena relación entre la calidad de la solución y el costo.
Quizás el punto más delicado de todo se encuentra en la definición de la función de evaluación, y de su eficacia depende el obtener buenos resultados. El resto del proceso es siempre el mismo para todos los casos.
La programación mediante algoritmos genéticos suponen un nuevo enfoque que permite abarcar todas aquellas áreas de aplicación donde no sepamos como resolver un problema:
Aplicaciones de búsqueda y optimización :
Desde aplicaciones evidentes, como la biología o la medicina, hasta otros campos como la industria (clasificación de piezas en cadenas de montaje). Los algoritmos genéticos poseen un importante papel en este ámbito.
Aprendizaje automático:
La capacidad que poseen para favorecer a los individuos que se acercan al objetivo, a costa de los que no lo hacen, consigue una nueva generación con mejores reglas y, por lo tanto el sistema será capaz de ir aprendiendo a conseguir mejores resultados. Es aquí donde encuentran un estupendo marco de trabajo los GA.
DiRECCIONES DE CONSULTA:
Algoritmos Genéticos
3
Un algoritmo genético consiste en hallar de qué parámetros depende el problema, codificarlos en un cromosoma, y se aplican los métodos de la evolución: selección y reproducción sexual con intercambio de información y alteraciones que generan diversidad. En las siguientes secciones se verán cada uno de los aspectos de un algoritmo genético.
Algoritmo genético
-
Evaluar la puntuación (fitness) de cada uno de los genes.
-
Permitir a cada uno de los individuos reproducirse, de acuerdo con su puntuación.
-
Emparejar los individuos de la nueva población, haciendo que intercambien material genético, y que alguno de los bits de un gen se vea alterado debido a una mutación espontánea.
Descargar
| Enviado por: | Cols |
| Idioma: | castellano |
| País: | España |
