Ingeniero Técnico en Informática de Sistemas
Transformada de Wavelet
Práctica 2a: Introducción a la transformada Wavelet.
Introducción.
En esta primera parte de la práctica realizaremos la transformada Wavelet de primer nivel de una imagen. El objetivo es ilustrar, de forma interactiva, el proceso de transformación y antitransformación de la imagen, comprobando que en el dominio transformado, los niveles de gris se concentran en áreas de la imagen muy reducidas de manera que pueden codificarse de forma muy eficiente. Utilizaremos unicamente una transformada de primer nivel en una imagen en blanco y negro para concentrarnos en los aspectos más significativos de la transformación y del análisis de las imágenes resultantes. En la práctica, para conseguir factores de compresión significativos, es conveniente utilizar la transformada en varias etapas. El ejercicio cubre sólo los aspectos más elementales de la codificación mediante wavelets, dejando los aspectos como cuantificación, SNR multiescala y resolución multiescala para una segunda parte de la práctica que se realizará con un programa de codificación mediante wavelets cerrado.
Carga y visualización de la imagen a procesar.
Realizaremos las pruebas con una imagen muy popular (Lena) en blanco y negro. La imagen está en formato bitmap con una resolución de 256x256 en el directorio de la práctica y con el nombre Pamela2.bmp. Las siguientes instrucciones realizan la carga de la imagen, la convierten a niveles de intensidad entre 0 (negro) y 1 (blanco) y la representan en pantalla.
[nom,path]=uigetfile('*.bmp');
a=imread([path,nom]);
b=double(a);
b=b/max(max(b));
imshow(b);
Primera etapa de la transformada directa.
Recordemos que el diagrama de bloques para la descomposición en subbandas de la imagen es:
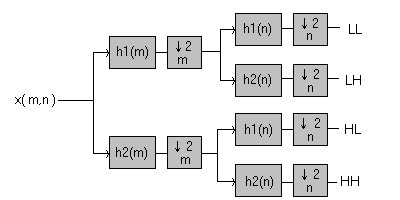
donde intervienen los filtros base h1(n) y h2(n) que pueden interpretarse como un filtro paso bajo y uno paso alto respectivamente. En este esquema, interpretaremos la dirección 'm' como la horizontal y la 'n' como la vertical, de modo que las matrices que representan las imágenes estarán indexadas como u(n,m) - n: fila, m: columna. Los símbolos de diezmado se indican con una flecha hacia abajo, especificando la dirección en la que se realiza la reducción de las imágenes. Los filtros h1 y h2 pueden ser cualesquiera que cumplan las condiciones exigidas por la transformada wavelet y que, por tanto, permitan recuperar la imagen original a partir de las imágenes transformadas. La pareja de filtros que se utiliza más a menudo pertenecen a la familia de Daubechies y pueden expresarse (en la dirección m - horizontal) como:
h1=[1/sqrt(2),1/sqrt(2)];
h2=[1/sqrt(2),-1/sqrt(2)];
En el primer caso, se trata de un filtro paso bajo de 9 coeficientes y simétrico. h2 es el filtro paso alto, que en este caso tiene sólo 3 coeficientes y es también simétrico.
Las imágenes en las salidas del primer bloque de filtros, antes de realizar el diezmado pueden calcularse como:
bh1=filter2(h1,b);
bh2=filter2(h2,b);
Obsérvese que las dos imágenes son una versión filtrada de la imagen original. En el primer caso, se ha realizado un suavizado en la dirección horizontal mientras en el segundo se han enfatizado los contornos verticales (filtro paso alto en la dirección horizontal).
figure(1); imshow(bh1/max(max(bh1)));
figure(2); imshow(bh2+0.5);
Nótese que debido a las características del filtrado, en la imagen de la banda de alta frecuencia se representa el cero como el nivel de gris medio. La imagen de baja frecuencia se normaliza debido a que el filtro paso bajo tiene una ganancia distinta de la unidad. La descomposición de la imagen original en estas dos subimágenes permite reducir la frecuencia de muestreo en la dirección horizontal sin que se produzca, como veremos posteriormente, pérdida de información. El diezmado de las dos imágenes se realiza con las siguientes instrucciones:
bh1m=bh1(:,1:2:256);
bh2m=bh2(:,1:2:256);
figure(1); imshow(bh1m/max(max(bh1m)));
figure(2); imshow(bh2m+0.5);
Nótese que al realizar el diezmado en la dirección horizontal se reduce la resolución, pasando a obtener imágenes de 256x128 píxeles.
Aplicaremos ahora los filtrados en la dirección vertical a cada una de las subimágenes obtenidas:
bh1mh1=filter2(h1',bh1m);
bh1mh2=filter2(h2',bh1m);
bh2mh1=filter2(h1',bh2m);
bh2mh2=filter2(h2',bh2m);
Ahora podemos aplicar el diezmado vertical a estas imagenes:
bLL=bh1mh1(1:2:256,:);
bLH=bh1mh2(1:2:256,:);
bHL=bh2mh1(1:2:256,:);
bHH=bh2mh2(1:2:256,:);
Estas imágenes se corresponden con las salidas del diagrama de bloques que representa el análisis por bandas de la transformada wavelet. Con el diezmado en las direcciones verticales y horizontales se han obtenido 4 imágenes de 128x128 puntos que representan la imagen original de 256x256. Esto, en principio, no supone ninguna compresión del número total de pixels. No obstante, veremos más adelante que las imágenes con alguna componente de alta frecuencia pueden codificarse de forma mucho más eficiente sin que se produzcan pérdidas de información.
Las imágenes resultantes de la descomposición en bandas son:
figure(1); subplot(221);imshow(bLL/max(max(bLL)));
subplot(222);imshow(bLH+0.5);
subplot(223);imshow(bHL+0.5);
subplot(224);imshow(bHH+0.5);
Obsérvese como en la imagen bLH predominan los contornos verticales, en la bHL los horizontales y en la bHH los diagonales.
La transformación inversa.
Las imágenes bLL, bLH, bHL y bHH constituyen una representación alternativa de la imagen original b. Podemos reconstruir esta imagen original a partir de las anteriores sin más que aplicar las operaciones de la transformación en orden inverso. El diagrama de bloques para restaurar la imagen original es:
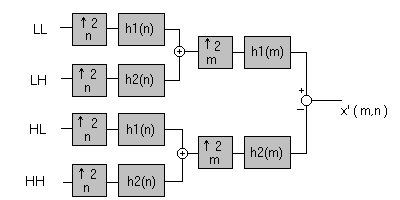
Seguiremos este esquema para obtener la imagen reconstruida br. En primer lugar intercalamos ceros en la dirección vertical de las imágenes de partida, obteniendo imágenes de 256x128 píxeles.
bLLin=zeros(256,128);bLLin(1:2:256,1:128)=bLL;
bLHin=zeros(256,128);bLHin(1:2:256,1:128)=bLH;
bHLin=zeros(256,128);bHLin(1:2:256,1:128)=bHL;
bHHin=zeros(256,128);bHHin(1:2:256,1:128)=bHH;
Podemos visualizar una de las imágenes resultantes para comprobar la correcta intercalación de los ceros:
imshow(bLLin/max(max(bLLin)))
Ahora filtramos las imágenes resultantes mediante h1 y h2 tal y como se indica en el diagrama de bloques de la figura anterior:
h2=[-1/sqrt(2),1/sqrt(2)];
(Nota: El filtro reconstructor paso alto tiene los coeficientes cambiados de orden)
bL1=filter2(h1',bLLin)+filter2(h2',bLHin);
bH1=filter2(h1',bHLin)+filter2(h2',bHHin);
Intercalamos los zeros en la dirección horizontal a cada una de las imágenes:
bLin=zeros(256,256); bLin(1:256,1:2:256)=bL1;
bHin=zeros(256,256); bHin(1:256,1:2:256)=bH1;
Y nuevamente filtramos y combinamos las imágenes para obtener la imagen reconstruida:
br = filter2(h1,bLin)+filter2(h2,bHin);
La imagen resultante resulta:
imshow(br/max(max(br)))
imshow(abs(b(2:256,2:256)-br(1:255,1:255)))
Lo cual indica que ambas imágenes son idénticas salvo el posible desplazamiento de un pixel, que se debe a los retardos introducidos por los filtros y que se puede estimar a priori.
Estudio estadístico de los datos transformados y manipulación de la imagen en el dominio transformado.
De acuerdo con los resultados anteriores, la imagen puede representarse mediante los datos contenidos en la matriz b (imagen original) o mediante los datos contenidos en las matrices bLL, bLH, bHL y bHH (imágenes transformadas). Nótese que hemos comprobado que a partir de este conjunto de matrices podemos recuperar exactamente la imagen original. La cuestión que abordamos ahora es ver cúal de las dos representaciones es más eficiente cuando el objetivo es almacenar la imagen en el disco duro o transmitirla a distancia.
Es importante comprobar que el número de elementos de imagen en las dos representaciones son idénticos. En efecto la imagen original tiene un total de 256x256 = 65.536 píxeles mientras que cada una de las imágenes transformadas tienen 128x128 = 16.384 pixeles que resulta en un total de 4x16.384 = 65.536 píxeles.
En consecuencia, la ventaja de una u otra representación debe encontrarse en la forma en que están distribuidos los niveles de gris de la imagen. Para estudiar esta distribución, analizaremos los histogramas de la imagen original y de las imágenes transformadas.
El histograma de la imagen original puede obtenerse directamente en el Matlab ejecutando la instrucción:
figure(1);imhist(b);
Los histogramas de las imágenes transformadas pueden obtenerse de forma parecida:
figure(2);subplot(221);imhist(bLL/max(max(bLL)));
subplot(222);imhist(bLH+0.5);
subplot(223);imhist(bHL+0.5);
subplot(224);imhist(bHH+0.5);
Estos resultados indican que tanto la imagen original como la bLL (versión paso bajo de las transformadas wavelet de primer nivel) tienen un histograma parecido y en el que aparecen con elevada probabilidad todos los posibles niveles de gris. Por tanto la eficiencia en la codificación de ambas imágenes es parecida, con la ventaja de que bLL tiene bastantes menos elementos de imagen que b.
Las versiones bLH, bHL y bHH tienen unos histogramas centrados principalmente en un entorno de cero (en las gráficas aparecen los picos alrededor de 0.5 puesto que hemos sumado el nivel de gris medio a las imágenes). Esto indica que pueden codificarse de forma muy eficiente utilizando códigos de longitud variable (Huffman o aritméticos) que aprovechen esta distribución. Así, podemos asignar palabras código de pocos bits a los valores próximos al cero (que son los que se producen con mayor frecuencia) y palabras código más largas a los valores elevados que se producen con menor frecuencia. Con ello, estas tres componentes (imágenes) de la transformada pueden codificarse utilizando un número mucho menor de bits que la componente de baja frecuencia. Por ello, resulta más rentable almacenar las cuatro componentes bLL, bHL, bLH y bHH que almacenar directamente la imagen original.
Hasta aquí, la representación de la imagen mediante las 4 componentes de su transformada wavelet no representa ninguna pérdida de información, pudiendo recuperar de forma exacta la imagen original a partir de sus transformadas. Otra ventaja de la transformada wavelet es que las componentes de alta frecuencia pueden almacenarse de forma aproximada sin que ello produzca pérdidas de calidad aparente en la imagen decodificada. En efecto, ahora aproximaremos las imágenes bLH, bHL y bHH en pasos de 0.1 unidades y veremos que no se observan grandes pérdidas en la reconstrucción de la imagen original. Para aproximar las componentes de alta frecuencia en pasos de 0.1 unidades utilizamos las siguientes instrucciones:
bLHa =round(bLH*10)/10;
bHLa =round(bHL*10)/10;
bHHa = round(bHH*10)/10;
Resulta fácil comprobar que los histogramas de las imágenes resultante toman ahora muchos menos valores, por lo que su codificación resultará muy eficiente.
figure(2);subplot(221);imhist(bLL/max(max(bLL)));
subplot(222);imhist(bLHa+0.5);
subplot(223);imhist(bHLa+0.5);
subplot(224);imhist(bHHa+0.5);
Para ver como esta reducción en el número de niveles ha afecta a la calidad de la imagen vamos a repetir el proceso de reconstrucción de la imagen partiendo de bLL, bLHa, bHLa y bHHa. El proceso es idéntico al que se ha utilizado en el apartado de reconstrucción exacta de la imagen original a partir de la transformada wavelet.
bLLin=zeros(256,128);bLLin(1:2:256,1:128)=bLL;
bLHin=zeros(256,128);bLHin(1:2:256,1:128)=bLHa;
bHLin=zeros(256,128);bHLin(1:2:256,1:128)=bHLa;
bHHin=zeros(256,128);bHHin(1:2:256,1:128)=bHHa;
bL1=filter2(h1',bLLin)+filter2(h2',bLHin);
bH1=filter2(h1',bHLin)+filter2(h2',bHHin);
bLin=zeros(256,256); bLin(1:256,1:2:256)=bL1;
bHin=zeros(256,256); bHin(1:256,1:2:256)=bH1;
bra = filter2(h1,bLin)+filter2(h2,bHin);
imshow(bra/max(max(bra)));
Ahora, la reconstrucción sólo es aproximada, pero los efectos de esta aproximación son poco visibles. Para comprobar la aproximación podemos comparar la imagen br, con la imagen original mediante el valor absoluto de la diferencia.
imshow(abs(b(2:256,2:256)-bra(1:255,1:255)))
Las diferencias sólo son aparentes cuando aumentamos la escala de la imagen diferencia en un factor 10:
imshow(10*abs(b(2:256,2:256)-bra(1:255,1:255)))
Nótese que, con la reconstrucción original, las diferencias con la imagen original son inapreciables aún que se multipliquen por este factor:
imshow(10*abs(b(2:256,2:256)-br(1:255,1:255)))
En resumen, hemos comprobado que las componentes de alta frecuencia de la transformada wavelet pueden codificarse de forma mucho más burda que los componentes de baja frecuencia sin que aparezcan pérdidas aparentes en la calidad de la imagen. Obsérvese que la mayor parte de los coeficientes de bLHa, bHLa y bHHa toman el valor cero, de modo que, en la práctica resulta conveniente codificar únicamente la posición y el valor de los elementos distintos de cero con lo que puede aumentarse todavía más el factor de compresión.
Transformación wavelet multiescala.
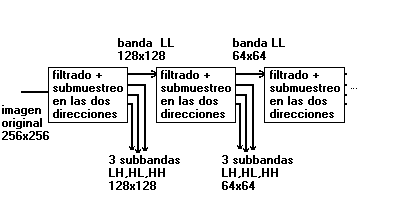
Hasta ahora, queda claro que hemos obtenido una importante ventaja en la codificación de la imagen mediante la representación que nos proporciona la transformada wavelet. No obstante, la imagen de baja frecuencia bLL, aún exige un elevado número de bits para su correcta codificación. La consecuencia lógica de estos resultados es evidente: podemos obtener considerables mejoras si aplicamos nuevamente esta representación alternativa a la imagen bLL. Con ello, obtendremos tres imágenes de alta frecuencia que podrán codificarse de forma muy eficiente y una nueva imagen de baja frecuencia (cada vez con menor número de píxeles) que deberemos codificar con precisión. La idea de aplicar este procedimiento a múltiples resoluciones se esquematiza en la figura siguiente.
Aplicaciones de la transformada wavelet en mejora de imágenes.
En este apartado veremos una forma de enfatizar los contornos de la imagen mediante la descomposición espectral de las imágenes. La idea básica consiste en repetir el proceso de reconstrucción de la imagen pero utilizando las componentes de alta frecuencia enfatizadas. El proceso de reconstrucción es el mismo que el expuesto en apartados anteriores por lo que se omiten los detalles. Las componentes de alta frecuencia se han multiplicado por un factor 2 para que el efecto de enfatización de contornos resulte muy evidente.
bLLin=zeros(256,128);bLLin(1:2:256,1:128)=bLL;
bLHin=zeros(256,128);bLHin(1:2:256,1:128)=2*bLH;
bHLin=zeros(256,128);bHLin(1:2:256,1:128)=2*bHL;
bHHin=zeros(256,128);bHHin(1:2:256,1:128)=2*bHH;
bL1=filter2(h1',bLLin)+filter2(h2',bLHin);
bH1=filter2(h1',bHLin)+filter2(h2',bHHin);
bLin=zeros(256,256); bLin(1:256,1:2:256)=bL1;
bHin=zeros(256,256); bHin(1:256,1:2:256)=bH1;
bra = filter2(h1,bLin)+filter2(h2,bHin);
imshow(bra/max(max(bra)));
figure(2); imshow(b);
MEMORIA DE LA PRÁCTICA.
Realice un breve resumen de los conceptos de compresión de imagen mediante transformada wavelet que se exponen en esta práctica.
Indique cuantos bits se requieren para codificar la imagen original y, de forma aproximada, cuantos se requerirían para codificar las imágenes bLHa, bHLa, bHHa. Proponga, basándose en los conocimientos de codificación que dispone, un procedimiento eficiente para codificar estas componentes de alta frecuencia.
Descargar
| Enviado por: | Frederic Alvarez |
| Idioma: | castellano |
| País: | Argentina |
