Física
Torque y centro de gravedad
Introducción.
El torque y el centro de gravedad. ¿Qué significan?
Esta es una pregunta que muchos se hacen al iniciar la materia de estática.
La fuerza aplicada a un cuerpo con un eje rotatorio es algo complicado de explicar, pero trataremos de ser precisos y entendibles a través de ejemplos de la vida diaria.
El centro de gravedad es algo que desalienta a cualquier principiante del tema, pero una vez entendido, resulta hasta casi agradable trabajar sobre el.
Esperamos que este trabajo sea de su agrado.
Torque.
Definición: Momento de fuerza o torque es el efecto giratorio que produce una fuerza aplicada a un cuerpo provisto de un eje.
Aplicaciones
Ejemplo Nº 1: Apretar una tuerca
Cuando una persona aprieta un tornillo con una llave, está aplicando un torque al tornillo. Como en el caso de la fuerza, si todos los torques son iguales, ella no podrá apretar el tornillo. Si el torque que ella aplica es mayor que el torque en contra debido a la fricción del tornillo, el tornillo rodará (se ajusta).
El torque y la fuerza están unidos directamente. Cuando la persona empuja (aplica una fuerza) al borde de la llave, cuanto más torque ella aplica más se ajusta el tornillo. Sin embargo, no es sólo la fuerza lo que hace la diferencia. Cuanto más distante del tornillo ella sostiene la llave, más torque aplica, y más se ajusta el tornillo. Por consiguiente, los torques se deben relacionar a la fuerza aplicada y a la distancia al centro de rotación donde se aplica la fuerza. Esta distancia se llama el brazo del momento.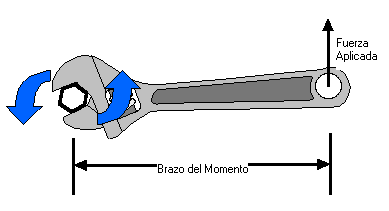
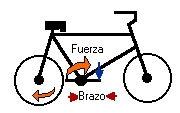
Ejemplo Nº 2: el pedal en la bicicleta
Empujando el pedal de la bicicleta transmite un torque que hace rodar los neumáticos. Si uno aplica un torque que exactamente neutraliza todos los otros torques (torques friccional, etc.) no se va a acelerar o desacelerar la velocidad del neumático (pedal).
(la suma de los torques = 0, por consiguiente la aceleración angular = 0)
si los torques friccional, etc. son mayores que el torque que uno aplica, se reducirá la velocidad del neumático (pedal).
(los torques se suman < 0, por consiguiente la aceleración angular < 0)
si el torque aplicado es mayor que el torque friccional, etc., el neumático (pedal) se va a acelerar.
(los torques se suman > 0, por consiguiente la aceleración angular > 0)
Ejemplo Nº3: La Puerta:
Una de las maneras de explicar el torque con un ejemplo cotidiano es observando bien cuando cerramos una puerta. Al cerrarla cerca de la chapa se nos hace muy fácil, debido a la extensión del brazo del momento, la cual es mayor que si cerramos la puerta cerca de las bisagras. Al hacerlo de esta forma se debe aplicar una fuerza mayor a la anterior.


Brazo Extenso Brazo corto
Menor Fuerza Mayor Fuerza
Centro de Gravedad.
Definición: punto de aplicación de la fuerza peso en un cuerpo, y que es siempre el mismo, sea cual sea la posición del cuerpo.
Para determinar el centro de gravedad hay que tener en cuenta que toda partícula de un cuerpo situada cerca de la superficie terrestre está sometida a la acción de una fuerza, dirigida verticalmente hacia el centro de la Tierra, llamada fuerza gravitatoria.
Cuando se trata de cuerpos de dimensiones muy pequeñas frente a la Tierra, se puede admitir que las fuerzas gravitatorias que actúan sobre las distintas partículas del cuerpo son paralelas y de módulo constante. Por tanto, se puede calcular la posición del centro de gravedad hallando la recta de acción de la resultante de esas fuerzas. Si el cuerpo es homogéneo, el centro de gravedad coincide con su centro geométrico.
Si un cuerpo es tan pequeño que la aceleración de la gravedad es la misma para todas las partículas, entonces el centro de masas y el de gravedad coinciden.
Determinación experimental: si un cuerpo esta estático y posee forma más o menos simétrica su centro de gravedad coincidirá con su centro geométrico
Conclusiones.
-
Este trabajo, según nuestra opinión, nos sirvió para complementarnos cada una de las ideas y opiniones de los demás compañeros del grupo.
-
Recordamos antiguos términos como fuerza, movimiento y demás.
-
Los términos como momento y centro gravitacional no son tan aburridos como todos creen, basta con aplicarlos en forma entretenida.
Descargar
| Enviado por: | Jorge Lopez |
| Idioma: | castellano |
| País: | Chile |
