Matemáticas
Teoría de matrices
Matemática.
Guía de aprendizaje: TEORIA MATRICIAL.
1. A qué se llama matriz matemática?
2. En una matriz, a que se llama?:
a. Elementos
b. Filas
c. Columnas
d. Diagonal Principal
3. A qué se llama vector fila y vector columna?
4. Cuando dos matrices son iguales?
5. Cómo se suman matrices?
6 a 11. Sumar matrices
12. Identificar y dar ejemplos de cada una de las siguientes propiedades matriciales:
A+B = B+A
A+B+C = (A+C)+B
A+0 = A
A+(-A) = 0
13. Cómo se restan matrices?
14 a 18. Restar matrices
19. Cómo se resuelve el producto escalar: n.Amxn
20. Qué propiedades son?:
n.Amxn = Mmxn
1.Amxn = Amxn
(-1).Amxn = -Amxn
21 a 24. Resolver productos escalares de matrices.
25. Cómo se multiplican vectores matriciales?
26. Qué condición se tiene que dar para poder multiplicar dos matrices?
27. Explicar cómo se multiplican matrices a través de un ejemplo. Dando las características de la matriz producto
28. Si manejas algún esquema práctico para multiplicar matrices, explícalo.
29 a 38. Multiplicar matrices, con crecientes dificultades.
39. A que se llama matriz inversa? Explicar, definir y ejemplificar
40. A qué se llama matriz transpuesta? Explicar, definir y ejemplificar
Matemática: Teoría matricial
1. Se llama matriz matemática al conjunto ordenado de elementos, en M filas y N columnas y se simboliza:
MxN
2. Los elementos son los números que constituyen la matriz. Y decimos que estos números ordenados en forma horizontal pertenecen a una fila, mientras que aquellos elementos ordenados en forma vertical pertenecen a una columna.
La diagonal principal es el conjunto de elementos dentro de la matriz, los cuales cumplen con la característica de que su lugar en la fila coincide con su lugar en la columna. Esta diagonal empieza en el elemento 11, siguiendo por el 22, y así sucesivamente, abarcando tantos elementos como filas posea la matriz.
3. Llamamos vector fila aquella matriz conformada por una sola fila, y vector columna a la matriz de una sola columna.
4. Dos matrices son iguales cuando poseen la misma cantidad de elementos, filas y columnas. Y sus elementos son iguales y ubicados en la misma posición dentro de la matriz(elementos homólogos)
5. La suma de matrices se realiza sumando de forma corriente los elementos homólogos de las matrices involucradas en la operación.
Recordemos que denominamos elementos homólogos aquellos números igualmente ubicados dentro de la matriz.
6-11. Por una cuestión práctica, los ejercicios se encuentran en hojas de carpeta cuadriculadas adjuntas a esta guía.
12. A+B = B+A : Propiedad conmutativa. Podemos alterar el orden de las matrices que participan en la suma, sin embargo el resultado no tendrá variaciones.
A+B+C = (A+C)+B : Propiedad asociativa. Es lo mismo sumar todas las matrices juntas, que al resultado de la suma de varias matrices sumarle otra matriz más.
A+0= A : La matriz nula es elemento neutro en la suma. Si tenemos una matriz nula(todos sus elementos son 0) la matriz no nula será el resultado de la suma de matrices.
A+(-A) = 0 : Existencia de elemento opuesto. Si a cualquier matriz se le suma su opuesto (-A), el resultado de la suma será nulo.
13. La resta de matrices se realiza sumándole el opuesto de la segunda matriz a la primer matriz dada.
14 a 18. Se encuentran en las hojas adjuntas a la guía
19. El producto escalar de n.Amxn se resuelve obteniendo el producto de cada uno de los elementos de la matriz por él numero real dado. Teniendo en cuenta que cada producto obtenido tendrá la misma ubicación en la matriz producto que el factor utilizado de la matriz dada.
20. n.Amxn = Mmxn : al multiplicar un numero real por una matriz obtendremos un matriz producto, del mismo orden que la primera.
1.Amxn = Amxn : si el elemento real dentro de la multiplicación es 1, la matriz producto será igual a la primer matriz
(-1).Amxn = -Amxn : Si el elemento real dentro de la multiplicación es -1, la matriz producto tendrá el mismo orden y misma cantidad de elementos que la primera, pero con distinto signo. En otras palabras, se obtendrá la matriz opuesta.
21 a 24. Se encuentran en las hojas adjuntas a la guía.
25. Para resolver una multiplicación entre vectores matriciales hay que multiplicar el primer elemento de la fila de la primer matriz por el primer elemento de la primer columna de la segunda matriz, y en forma similar, los restantes elementos, para luego sumar los productos obtenidos y llegar así a un resultado, el cual tendrá un orden determinado por él numero de fila y columna involucradas en la operación.
26. Para resolver una multiplicación de vectores matriciales hay que saber que solo se pueden multiplicar filas por columnas, siendo posible solo este orden y no pudiendo ser filas por filas, columnas por columnas o columnas por filas. SOLO FILAS POR COLUMNAS.
Otra condición es que debe coincidir el número de columnas de la primer matriz con el numero de columnas de la segunda
27.
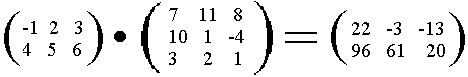
a11= (-1.7)+(2.10)+(3.3) = 22
a12= (1.11)+(2.1)+(3.2) = -3
a13= (-1.8)+(2.-4)+(3.1) = -13
a21= (4.7)+(5.10)+(6.3) = 96
a22= (4.11)+(5.1)+(6.2) = 61
a23= (4.8)+(5.-4)+(6.1) = 20
-
La matriz obtenida tendrá tantas filas como el primer factor y tantas columnas como el segundo
28 a 38. Se encuentran en las hojas adjuntas a la guía.
39. Podemos decir que una matriz inversa es aquella a la que hay que multiplicar una matriz cuadrada para que su resultado posea las siguientes características:
-
Matriz producto de orden Amxm(matriz cuadrada)
-
Su diagonal principal esta conformada solo por 1
-
Todos sus elementos excepto la diagonal principal son 0
Ejemplo:
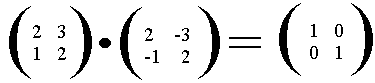
Si bien para encontrar una matriz inversa debemos saber operar con determinantes, a continuación explico como encontrar la matriz inversa de una matriz de orden 2 y solo de este orden, ya que a medida que aumentamos la cantidad de elementos, también aumenta la cantidad de cálculos necesarios para resolver la operación:
Referencia:
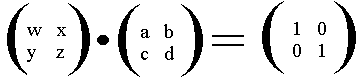
W: elemento a11 de la matriz A
X: elemento a12 de la matriz A
Y: elemento a21 de la matriz A
Z: elemento a22 de la matriz A
A: elemento b11 de la matriz B
B: elemento b12 de la matriz B
C: elemento b21 de la matriz B
D: elemento b22 de la matriz B
De aquí se deducen dos sistemas de ecuaciones con las incógnitas “a” y “c” para el primer sistema y con “b” y “d” para el segundo, suponiendo que conocemos los elementos de la matriz A
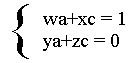
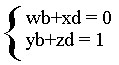
Del primer sistema resulta:
![]()
![]()
Aplicando el método de igualación:
![]()
![]()
![]()
De esta forma obtenemos “a”, para luego poder encontrar “c” por medio de la resolución de una de las dos ecuaciones resultantes del primer sistema:
![]()
![]()
Mientras que del segundo sistema de ecuaciones deducimos:
![]()
![]()
y al realizar igualación obtenemos que:

de manera análoga a “c”, resolvemos uno de los sistemas de ecuaciones
![]()
![]()
Ahora bien, estas formulas solo sirven si todos los elementos de la primer matriz excepto w(a11) son diferentes a 0 ya que si x, y o z son iguales 0, en cualquiera de las operaciones obtenidas para encontrar “a” o “b” estos elementos son utilizados como divisores y se sabe que no se puede dividir por 0.
Ejemplo

Utilizando la primer fórmula obtenida:
En este caso será imposible encontrar “a”, ya que esto requiere dividir -1 y -w(-2) por x(0), operación que no tiene solución.
Y utilizando la segunda:

Tampoco podremos hallar “b”, ya que esto requiere dividir w(2) por x(0) y es una operación idéntica a la anterior; no posee solución.
Hay que tener en cuenta que este es un método muy poco practico si se sabe operar con determinantes, pero por el momento no lo sabemos hacer, así que es el único método que tenemos para encontrar una matriz inversa de orden 2.
40. La matriz transpuesta Amxn se obtiene colocando la primera fila de A como primer columna, y en forma similar, las restantes. Obteniendo así una matriz Anxm.
A la matriz transpuesta de A se la simboliza:
![]()
Ejemplo:


Bibliografía utilizada:
-
Matemática II. De Buschiazzo y otros. Editorial Santillana. Capítulos 3 y 4
-
Álgebra I, de Zill y Dewar. Editorial McGrawHill. Capítulos 9 y 10
Descargar
| Enviado por: | Pitu |
| Idioma: | castellano |
| País: | Argentina |
