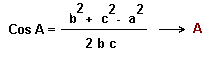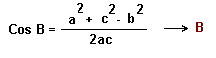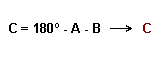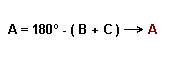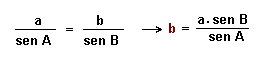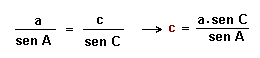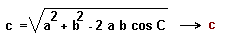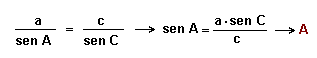Matemáticas
Teoremas del seno y del coseno
Teoremas del seno y del coseno
Introducción:
-
Trigonometría
Rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos; etimológicamente significa `medida de triángulos'.
Las primeras aplicaciones de la trigonometría se hicieron en los campos de la navegación, la cartografía y la astronomía, en los que el principal problema era determinar una distancia inaccesible, es decir, una distancia que no podía ser medida de forma directa, como la distancia entre la Tierra y la Luna. Se encuentran notables aplicaciones de las funciones trigonométricas en la física y en casi todas las ramas de la ingeniería, sobre todo en el estudio de fenómenos periódicos, como el flujo de corriente alterna.
Las dos ramas fundamentales de la trigonometría son la trigonometría plana y la trigonometría esférica…
Trigonometría plana:
Se ocupa fundamentalmente de la resolución de triángulos planos. Para ello, se definen las razones trigonométricas de los ángulos y se estudian las relaciones entre ellas.
Trigonometría esférica:
La trigonometría esférica, que se usa sobre todo en navegación y astronomía, estudia triángulos esféricos, es decir, figuras formadas por arcos de circunferencias máximas contenidos en la superficie de una esfera. El triángulo esférico, al igual que el triángulo plano, tiene seis elementos: los tres lados a, b, c, y los tres ángulos A, B y C. Sin embargo, los lados de un triángulo esférico son magnitudes angulares en vez de lineales, y dado que son arcos de circunferencias máximas de una esfera, su medida viene dada por el ángulo central correspondiente. Un triángulo esférico queda definido dando tres elementos cualesquiera de los seis, pues, al igual que en la geometría plana, hay fórmulas que relacionan las distintas partes de un triángulo, que se pueden utilizar para calcular los elementos desconocidos.
-
Triángulos oblicuángulos
Se contrapone a rectángulo, en sentido estricto. Pero cuando se habla de triángulos oblicuángulos no se pretende excluir al triángulo rectángulo en el estudio, que queda asumido como caso particular. No obstante cuando el triángulo es rectángulo, porque se dice expresamente que lo es, el problema se reduce, tiene un tratamiento particular y no se aplican las técnicas generales de resolución que vamos a ver seguidamente.
Los elementos de un triángulo oblicuángulo son los tres ángulos A, B y C y los tres lados respectivos, opuestos a los anteriores, a, b y c.
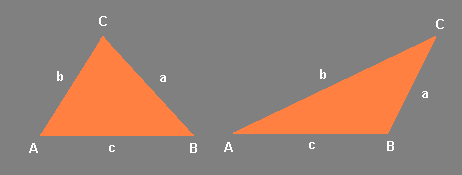
Para resolver específicamente TRIÁNGULOS OBLICUÁNCULOS, son utilizados los teoremas del seno y del coseno, los cuales a continuación serán desarrollados y pertenecen a la ya mencionada “trigonometría plana”…
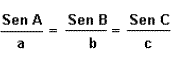
| Teorema del seno |
|
| Teorema del coseno | a2 = b2 + c2 - 2 b c Cos A b2 = a2 + c2 - 2 a c Cos B c2 = a2 + b2 - 2 a b Cos C |
Teniendo además siempre en cuenta que:
| La suma de los ángulos interiores de un triángulo | A + B + C = 180º |
EJEMPLOS:
| CASO | DATOS CONOCIDOS | INCÓGNITAS |
| Los tres lados: a, b, c | Los tres ángulos A, B, C | |
| Un lado y los ángulos adyacentes: a, B, C | Dos lados y un ángulo: b, c, A | |
| Dos lados y el ángulo formado: a, b, C | Un lado y dos ángulos: c, A, B | |
| Dos lados y el ángulo opuesto | Un lado y dos ángulos: c, B, C |
Resoluciones:
CASO I
La solución trigonométrica de A, B y C se obtiene calculando en el siguiente orden:
1º Aplicando el teorema del coseno para calcular A y luego B
2º Aplicando la relación de la suma de ángulos se calcula C:
|
|
|
|
CASO II
La única limitación es que los dos ángulos tienen que sumar menos de 180º (B + C < 180º) para que sea posible la construcción.
En la escena los parámetros son a, B y C que inicialmente tiene el valor a = 10, B = 45º, C = 76º.
La solución trigonométrica se consigue aplicando el siguiente orden a las propiedades:
1º Suma de los ángulos B + C para determinar A
2º Teorema del Seno para determinar sucesivamente los lados b y c.
|
|
|
|
CASO III
La solución trigonométrica se consigue aplicando en el mismo orden las siguientes propiedades:
1º Teorema del coseno para calcular el lado c,
2º Teorema del seno para calcular el ángulo A
3º Una vez conocidos A y C, la propiedad de la suma de los tres ángulos para calcular B.
|
|
|
|
CASO IV
Este caso es el más complejo ya que se pueden dar tres situaciones:
-
No existe triángulo
-
Existe un triángulo
-
Existen dos triángulos.
Suponemos conocidos los lados a y b y el ángulo A opuesto al lado a.
La solución trigonométrica se consigue aplicando las siguientes propiedades en el mismo orden:
1º Teorema del seno para calcular el ángulo B
2º La propiedad de la suma de los tres ángulos para calcular C
3º Nuevamente el Teorema del seno para calcular el lado c
|
|
|
|
Fuentes de información:
-
http://es.encarta.msn.com/text_761572350__1/Trigonometr%C3%ADa.html
-
"Trigonometría," Enciclopedia Microsoft® Encarta® Online 2005
http://es.encarta.msn.com © 1997-2005 Microsoft Corporation. Reservados todos los derechos.
Descargar
| Enviado por: | Luch |
| Idioma: | castellano |
| País: | Argentina |