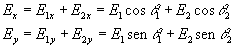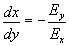Física
Superficies equipotenciales
SUPERFICIES EQUIPOTENCIALES
INDICE
Introducción
Objetivos
Reseña Histórica
Marco Teórico
Elementos Utilizados
Procedimientos
Datos Obtenidos
Procedimientos de Datos / Resultados
Conclusiones
10-Aplicaciones a la Carrera
11-Bibliografía
INTRODUCCIÓN
Este trabajo se ha expuesto después de una practica de laboratorio con el fin de investigar y aclarar aquellas dudas que quedaron expuestas en el, su comportamiento y su definición en general.
Con esto también queremos llegar a estructurar aquella dudas que se crearon en el laboratorio , por que con ello podemos entender mas sobre las superficies equipotenciales y en que nos puede ayudar y sobre todo para que nos sirve o en que la podemos aplicar ya sea en nuestra vida o en la carrera ; pero con este trabajo lo que pretendemos es ampliar un poco mas lo que es en si las equipotencias y cuales formulas se pueden aplicar o mas bien cuales se aplica como reglas generales para los equipotenciales , para llegar a elaborar un laboratorio bien fundamentado .
RESEÑA HISTORICA
El primer fenómeno eléctrico observado, la acción del ámbar frotado sobre los cuerpos livianos , se conoce desde la antigüedad. Thales de Mileto, en 600 a. de C., fue el primero en describirlo. Veinte siglos después, no se sabia nada mas.
En 1600, el ingles Gilibert concluyo que no solamente el ámbar frotado presenta la característica de atraer los cuerpos livianos sino también muchos otros cuerpos y los llamo eléctricos. Noto la influencia de la humedad sobre los fenómenos eléctricos y fue el primero en separar los fenómenos eléctricos delos magnéticos.
Mas tarde , Otto de Guericke fabrico la maquina eléctrica; consistía en una bola de azufre que se hacia girar entre las dos manos para producir el rozamiento necesario. Con esta maquina primitiva realizo varios experimentos y en especial chispas.
En 1729, el ingles Gray descubrió la Conductividad de algunas sustancias como los metales y la no conductividad de otra sustancias como la seda, descubrió el fenómeno de la Inducción.
En 1733, el francés Dufay mostró que existen dos clases de electricidad que el nombro vidriosa y resinosa y enuncio que las cargas del mismo nombre se repelen y las de distinto nombre se atraen. Señalo que la electricidad se escapa de los cuerpos incandescentes: es el efecto termoiónico.
En 1746, el alemán Musschenbroek descubrió la condensación de la electricidad por medio de su botella de Leyden; fue el primer condensador.
El americano Franklin (1706-1790) sin conocer la teoría de Dufay creo que los cuerpos contenían una cantidad bien definida de un solo fluido eléctrico constituido por partículas eléctricas. La electrización consistía bien en que el cuerpo contenía una cantidad extra de fluido y quedaba electrizado positivamente o parte del fluido o quedaba electrizado negativamente.
Los progresos ulteriores fueron esencialmente matemáticos, sugeridos por la resolución de los problemas eléctricos.
En 1777, el francés Lagrange definió el concepto de exponencial y mostró como del potencial se deduce el campo eléctrico y las fuerzas sobre los cuerpos.
En 1782, el francés Laplace mostró que esta función potencial satisface, fuera de toda carga , a una famosa ecuación llamada la Ecuación de Laplace; ecuación que se generalizo a otros campos de la física y de la matemática.
En 1813, el francés Poisson extendió esta ecuación a las regiones que contienen las cargas y estableció la ecuación de Poisson mas general que la de Laplace.
Esta ecuación es reencontrada, mas tarde, por el alemán Gauss, en 1839, bajo otra forma; es el teorema de Gauss del flujo eléctrico que sale de una superficie cerrada.
Finalmente, el ingles Green profundizo en el concepto de potencial, definió varias funciones de Green y demostró algunos teoremas (que llevan su nombre) necesarios para la resolución de lo problemas mas complejos de física y matemática.
ENERGIA POTENCIAL ELECTRICO
Analicemos el concepto de energía potencial gravitacional. Para esto, consideremos una masa m dentro del campo gravitacional g de la tierra. La fuerza que actúa sobre la masa es w=mg y el trabajo de la masa, cuando se desplaza de una altura inicial ho a una altura final h siguiendo el camino vertical AB=s de la figura 5.42ª, es:
W=mgs =mg (ho - h) =mgho - mgh
Se nota que el trabajo realizado por el peso ( se puede también decir realizado por el campo gravitacional de la tierra) es igual a la diferencia de una determinada cantidad mgh=Ep , llamada Energía Potencial del objeto en el campo gravitacional de la tierra.
De la misma manera, consideremos una carga q dentro de un campo eléctrico uniforme horizontal E, siguiendo el camino horizontal AB=s de la figura 5.42b. La fuerza que actúa sobre la carga es Ff=qE y el trabajo de fuerza es:
W=Fs=qEs=qE(ho - h) = qEho - qEh
A F=qE B
+q 0
s h
h0
El trabajo realizado por la fuerza es igual a la diferencia de una determinada cantidad qEh=Ep, llamada energía potencial eléctrica de la carga en el campo eléctrico uniforme E.
Evidentemente la energía potencial es un punto se definirá si elegimos un punto de referencia Arbitrario y le asignamos la energía potencial cero.
Este concepto es valido cualquiera que sea la trayectoria entre A y B.
EJERCICIO
¿Cuál es el trabajo realizado por la fuerza F producida por un campo eléctrico constante E=300 N/C sobre una carga q=5 x 10-6C, cuando esta se desplaza, en la dirección del campo, una distancia s=20cm=0,02m?
SOLUCIÓN
Como el campo es constante , la fuerza F=Eq también es constante en la dirección del campo y , por tanto, en la dirección del desplazamiento s. El trabajo F es:
W=Fs=Eqs=300x5x10-6x0,02
=3x10-5J
EQUIPOTENCIALES
Dentro de un conductor cargado. E es cero; por tanto, la fuerza sobre una carga +q es F=Eq=0 y el trabajo de esta fuerza entre a (un punto de la superficie) y b (un punto interno) es W=0. La diferencia de potencial entre a y b es por tanto:
Va-Vb=W/q=0 ; Va=Vb
Como estos puntos son arbitrarios, esto indica que el potencial de cualquier punto de un conductor cargado tiene e mismo potencial ; diremos entonces, que es un volumen equipotencial.
Se demostró en la sección 5.1 que el campo eléctrico de un conductor cargado es normal a la superficie . Sobre una carga +q situada sobre la superficie. Por tanto , el ángulo entre F y cualquier desplazamiento sobre la superficie es 90º y el trabajo entre a y c (dos puntos de la superficie) es W=0. La diferencia de potencial entre a y c es por tanto:
Va-Vc=W/q=0 ; Va=Vc
Por consiguiente, reuniendo los dos resultados , se tiene:
Va=Vb=Vc
La superficie de un conductor es equipotencial y del mismo potencial que el del volumen que encierra.
DIFERENCIA DE POTENCIAL ES UN CONDENSADOR PLANO
Se sabe que en un condensador plano cargado, el campo E es uniforme. La fuerza que actúa sobre una carga +q es F=Eq y el trabajo que hace esta fuerza cuando se desplaza de a a b es:
W=Fs=Eqs
Y la diferencia de potencial es:
Vab=W/q=Eqs/q=Es
POTENCIAL PRODUCIDO POR UNA CARGA PUNTUAL
Una carga puntual produce alrededor de ella , en cada punto del espacio, un potencial eléctrico (como también un campo eléctrico).
Aquí, el campo eléctrico es variable y, por tanto, la fuerza también. El calculo del trabajo y por tanto el de la diferencia de potencial es mas delicado y se hace dividiendo el trayecto en una infinidad de pequeños intervalos , considerando el campo constante en cada intervalo y efectuando la suma de todos los trabajos elementales.
El resultado es que si se toma como potencial de referencia el potencial de un punto del infinito y si se le asignan el valor cero, el potencial en un punto a debido a una carga puntual q y a una distancia ra de ella, es:
Va=K q
ra
El potencial en un punto P debido a varias cargas puntuales q1,q2,q3 situadas a las distancias r1,r2,r3 de P, es la suma algebraica de los potenciales debidos a cada carga ; o sea
Vp=K q1 + q2 + q3
r1 + r2 + r3
CAMPO ELÉCTRICO Y POTENCIAL DE UNA
CARGA PUNTUAL
El fisica/elecmagnet/campo_electrico/campo/campo.htm">campo eléctrico de una carga puntual Q en un punto P distante r de la carga viene representado por un vector de
![]()
-
módulo vale
-
dirección radial
-
sentido hacia afuera si la carga es positiva, y hacia la carga si es negativa
El potencial del punto P debido a la carga Q es un escalar y vale
![]()
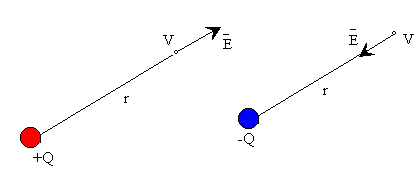
Un campo eléctrico puede representarse por líneas de fuerza, líneas que son tangentes a la dirección del campo en cada uno de sus puntos.
En la figura, se representan las líneas de fuerza de una carga puntual, que son líneas rectas que pasan por la carga. Las equipotenciales son superficies esféricas concéntricas.
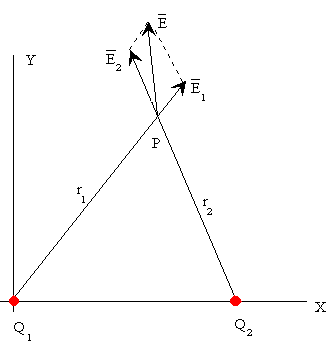
CAMPO ELÉCTRICO DE UN SISTEMA DE DOS CARGAS ELÉCTRICAS
| Cuando varias cargas están presentes el campo eléctrico resultante es la suma vectorial de los campos eléctricos producidos por cada una de las cargas. Consideremos el sistema de dos cargas eléctricas de la figura. El módulo del campo eléctrico producido por cada una de las cargas es
Y las componentes del campo total son
| |
|
|
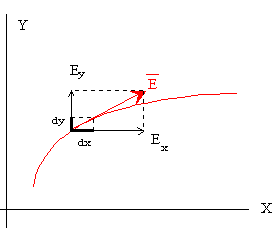
| Como el campo es tangente a las líneas de fuerza, la ecuación de las líneas de fuerza es
|
El potencial en el punto P debido a las dos cargas es la suma de los potenciales debidos a cada una de las cargas en dicho punto.
![]()
| Las superficies equipotenciales cortan perpendicularmente a las líneas de campo. Representaremos las líneas resultado de la intersección de las superficies equipotenciales con el plano XY. A partir de la figura puede deducirse la ecuación de las líneas equipotenciales
|

APLICACIONES A LA CARRERA
Desarrollo de prácticas para implementación de fuerzas en motores donde a partir del campo generado se aplica en turbinas, controles, generadores, circuitos eléctricos y electrónicos de sistema operativos y de mantenimiento para elaboración y funcionamiento en aviones y demás aplicaciones de orden mecánico inducido.
Además para cálculos de diferencias en estructuras y mecanismos ocasionados por cambios externos o de medio ambiente que inciden en el desempeño óptimo mecánico eléctrico de partes fundamentales en diseño e ingeniería aeronáutica entre otras.
CONCLUSIÓN
-
Evidencie como actúa un campo eléctrico en un pequeño experimento.
-
Analice el concepto de energía potencial , de equipotenciales,
-
Entendí y analice lo que el laboratorio significa para comprender un proceso bien.
-
Estudie aquello de que el campo eléctrico de un conductor cargado es normal a la superficie.
-
Explicar que son superficies equipotenciales y que queremos decir cuando decimos campo eléctrico.
-
Construir un análisis completo sobre el complejo tema de potencial eléctrico.
BIBLIOGRAFÍA
-
Michel Valero. Física 2 fundamental , Grupo Editorial Norma
Educativa . 1996
-
Michel Valero. Física 2 fundamental , Grupo Editorial Norma
Educativa . 1982
A
S
oB
ho
mg
h
O
FIGURA 5.42 a
FIGURA 5.42 b
Descargar
| Enviado por: | Bellis |
| Idioma: | castellano |
| País: | Colombia |