Matemáticas
Sistemas Lineales Invariantes en el Tiempo
SISTEMAS L.T.I.
• INTRODUCCIÓN:
Gran parte de los sistemas físicos reales se pueden aproximar a sistemas lineales tiempo invariantes(LTI). Como circuitos lineales o sistemas mecánicos. Por ello es muy importante el estudio del comportamiento de dichos sistemas, y como podemos manejarlos.
• REPRESENTACIÓN DE SEÑALES MEDIANTE IMPULSOS:
Es posible representar cualquier señal en tiempo discreto como una suma de Deltas de Kronecker. Para ello basta recordar que:
![]()
Con lo que en general podemos decir que:
![]()
En tiempo continuo la situación es un poco más complicada. Para estudiarla hacemos una aproximación:
Tomamos la función ![]()
, y escalonamos la señal a procesar, como en la imagen:
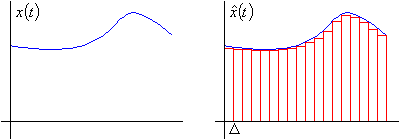
Con ello nos queda que:
![]()
Haciendo tender ![]()
a cero:
![]()
Es decir, podemos expresar una señal, tanto de tiempo discreto como continuo, mediante una suma de deltas de Kronecker o de Dirac según corresponda.
• RESPUESTA AL IMPULSO DE UN SISTEMA Y CONVOLUCIÓN:
• TIEMPO DISCRETO:
Supongamos un sistema lineal. Si de dicho sistema yo conozco la respuesta a la delta desplazada, es decir, conozco:
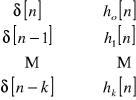
entonces, dada una secuencia tal como:
![]()
La respuesta del sistema a ![]()
será:
![]()
Si además el sistema es invariante en el tiempo, es decir:

Y conocemos ![]()
, entonces podemos conocer la respuesta del sistema ante cualquier señal. Para ello:
![]()
Y a esa operación, representada por “![]()
“ se le llama Suma de convolución. Como sabiendo ![]()
conocemos el comportamiento del sistema ante cualquier señal, definiremos los sistemas LTI mediante ![]()
, llamada respuesta al impulso del sistema. Además, toda propiedad de la convolución será aplicable a los sistemas.
Veamos entonces las propiedades de los sistemas:
Conmutativa:
![]()
Es decir:

Asociativa:
![]()
Es decir:

Distributiva respecto de la suma:
![]()
Es decir:

Ejemplo:
Sean una señal ![]()
y un sistema dado por ![]()

Operamos:
![]()
![]()
:

![]()
Análogamente nos queda:
|
|
|
|
|
|
|
|
|
|
|
|
Y la señal final queda como:

Siempre se verifica que el número de muestras de la señal resultante es el número de muestras de la señal de entrada más el de la respuesta del sistema menos uno. Por otra parte, existen infinitos sistemas cuya respuesta el impulso es la misma, pero solo existe uno que además sea lineal.
• TIEMPO CONTINUO:
Supongamos un sistema lineal. Si de dicho sistema yo conozco la respuesta a la delta desplazada, es decir, conozco:

entonces, el resultado de introducir a dicho sistema una señal ![]()
será:
![]()
Si además el sistema es tiempo invariante, es decir:

Entonces:
![]()
Y a esa operación, representada por “![]()
“ se le llama Integral de convolución. Las características y propiedades son análogas a las de la suma de convolución.
Ejemplo:

La integral se divide en varios trozos:
![]()
![]()
![]()

![]()
![]()

![]()
![]()

![]()
La señal resultante es:

• PROPIEDADES DE LOS SISTEMAS LTI:
Intentamos hallar un método para hallar las propiedades de un sistema mediante su respuesta al impulso. Para ello vamos a estudiar las propiedades y la convolución:
![]()
![]()
Memoria:
Sabemos que:
![]()
Por tanto la única manera de que la salida solo depende de la entrada actual es que:
![]()
Y en tiempo continuo:
![]()
Sistema inverso:
Partimos de:
![]()
Lo que buscamos es ![]()
tal que:
![]()
![]()
Si logramos encontrar una función que cumpla dicha condición, entonces la función tendrá inversa.
Causalidad:
La respuesta solo puede depender de valores actuales o anteriores, es decir:
![]()
Es decir, ![]()
no debe depender de ![]()
para ![]()
. Eso significa que todos los coeficientes ![]()
que multiplican a ![]()
para ![]()
han de ser nulos. Por tanto se ha de cumplir que ![]()
para ![]()
. Análogamente en tiempo continuo se ha de verificar que ![]()
para ![]()
.
Estabilidad:
Ha de ocurrir que ante valores acotados de la entrada, la salida este acotada. Por tanto:
![]()

Donde ![]()
Luego para que un sistema sea estable ha de ocurrir:
• DEFINICIÓN DE UN SISTEMA MEDIANTE EC. DIFERENCIALES:
• TIEMPO CONTINUO:
Es posible describir un sistema lineal mediante ecuaciones diferenciales con coeficientes constantes, es decir, definirlos mediante una ecuación de la forma:

Pero dicha ecuación no nos definirá el sistema por completo. Necesitamos unas condiciones iniciales para determinarlos por completo. Un claro ejemplo sería un circuito RLC, en el que habría que saber la carga inicial del condensador.
Dada una ecuación diferencial, el sistema que representa solo es lineal si las condiciones iniciales dadas son nulas.
• TIEMPO DISCRETO:
Igualmente es posible describir un sistema discreto mediante una ecuación en diferencias, cuya forma es:
![]()
De tal manera que es posible escribir la solución ![]()
como la suma de una solución particular de la ecuación dada más la solución general de la ecuación homogénea, y hacer:

Y aplicando condiciones auxiliares tendremos el sistema descrito.
El método para la resolución de dichas ecuaciones en diferencias es:

Con lo que obtenemos una formula recursiva.
Hay un caso particular, en el que el sistema viene descrito por la ecuación:

En esta caso no se necesitan condiciones iniciales, al venir totalmente determinado por la ecuación, ya que podemos hacer:

Y ya tenemos totalmente determinado el sistema.
Veamos un ejemplo de uso de la fórmula recursiva:
![]()
![]()
Condición inicial.
Introducimos una señal del tipo:
![]()
Hallamos la señal de salida:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
La señal total queda como:
![]()
![]()
![]()
Esta señal no es lineal, pues las condiciones iniciales no son nulas. Si es invariante en el tiempo.


Descargar
| Enviado por: | Josel pepelu |
| Idioma: | castellano |
| País: | España |
