Ingeniero en Informática
Sistemas Digitales
INDICE
REPRESENTACIONES NUMÉRICAS
Representaciones analógicas
Representaciones digitales
SISTEMAS DIGITALES Y ANALÓGICOS
SISTEMAS DE NÚMEROS DIGITALES
Sistema Decimal
Sistema Binario
REPRESENTACIÓN DE CANTIDADES BINARIAS
CIRCUITOS DIGITALES INTEGRADOS
TRANSMISIÓN PARALELA Y SERIAL
CONVERSIONES DE BINARIO A DECIMAL
CONVERSIONES DE DECIMAL A BINARIO
CONVERSIONES DE DECIMALES
CONVERSIÓN DE HEXADECIMAL A DECIMAL
CONVERSIÓN DE BINARIO A HEXADECIMAL
COMPUERTAS
AND
NAND
OR
NOR
NOT
BUFFER
REPRESENTACIONES NUMÉRICAS
En la ciencia, la tecnología, la administración y muchos otros campos de la actividad humana, constantemente se manejan cantidades. Existen básicamente dos maneras de representar el valor numérico de las cantidades: la analógica y la digital.
Representaciones analógicas. En la representación analógica, una cantidad se representa con un voltaje, corriente o movimiento de un indicador o medidor que es proporcional al valor de esa cantidad. Un ejemplo de esto es el velocímetro de un automóvil , en el cuál la deflexión de la aguja es proporcional a la velocidad a la que se desplaza el auto. La posición angular de la aguja representa el valor de la velocidad del automóvil, y la aguja sigue cualquier cambio que ocurra conforme el vehículo acelera o frena.
Otro ejemplo es el micrófono de audio. En este dispositivo se genera un voltaje de salida en proporción con la amplitud de las ondas sonoras que chocan con el micrófono. Las variaciones en el voltaje de salida siguen las mismas variaciones del sonido de entrada.
Las cantidades analógicas tienen una característica importante: pueden variar gradualmente sobre un intervalo continuo de valores. LA velocidad del automóvil puede tener un valor entre cero y, digamos, 100 km/hr. En forma análoga, la salida del micrófono podría encontrarse en cualquier nivel dentro de un intervalo de cero a 10mV (por ejemplo: 1mV, 2.3724 mV, 9.9999mV).
Representaciones digitales. En la representación digital las cantidades no se representan por valores proporcionales, sino por símbolos denominados dígitos.
Como ejemplo tenemos el reloj (o cronómetro) digital, el cuál da la hora del día en forma de dígitos decimales que representan horas o minutos ( y algunas veces segundos). Como sabemos, la hora varia de manera continua, pero la lectura del cronómetro digital no cambia continuamente: más bien, más bien los hace en etapas de uno por minuto (o por segundo). En otras palabras, esta representación digital de la hora varía en etapas discretas, comparada con la representación analógica de la hora que da un reloj de pulso, donde la lectura cuadrante varía de modo continuo.
La diferencia principal entre las cantidades analógicas y las digitales se puede enunciar en forma simple de la siguiente manera:
Analógico = continuo
Digital = discreto(paso por paso)
Debido a la naturaleza discreta de las representaciones digitales, no existe ambigüedad cuando se lee el valor de una cantidad digital, mientras que el valor de una cantidad analógica con frecuencia esta abierta a interpretación.
SISTEMAS DIGITALES Y ANALÓGICOS
Un sistema digital es una combinación de dispositivos diseñado para manipular cantidades físicas o información que estén representadas en forma digital; es decir, que sólo puedan tomar valores discretos. La mayoría de las veces estros dispositivos son electrónicos, pero también pueden ser mecánicos, magnéticos o neumáticos . Algunos de los sistemas digitales más conocidos incluyen las computadoras y las calculadoras digitales, equipo digital de audio y video y el sistema telefónico, el sistema digital, más grande del mundo.
Un sistema analógico contiene dispositivos que manipulan cantidades físicas representadas en forma analógica. En un sistema de este tipo, las cantidades varían sobre un intervalo continuo de valores. Por ejemplo, en un receptor de radio la amplitud de la señal de salida para una bocina puede tener cualquier valor entre cero y su límite máximo. Otros sistemas analógicos comunes son amplificadores de audio, equipos de cinta magnética para grabación y reproducción y el odómetro (cuenta kilómetros ) de los automóviles.
SISTEMAS DE NÚMEROS DIGITALES
En la tecnología digital se utilizan muchos sistemas de números. Los más comunes son los sistemas decimal, binario, octal y hexadecimal. El sistema decimal es sin duda el más conocido por nosotros, ya que es una herramienta de uso cotidiano.
SISTEMA DECIMAL. El sistema decimal se compone de 10 numerales o símbolos: 0,1,2,3,4,5,6,7,8 y 9; al utilizar estos símbolos como dígitos podemos expresar cualquier cantidad. El sistema decimal también conocido como sistema de base 10, evolucionó en forma natural a partir del hecho de que el ser humano tiene 10 dedos. Incluso, la palabra “dígito” significa “dedo” en latín.
El sistema decimal es un sistema de valor posicional en el cual el valor de un dígito depende de su posición.
SISTEMA BINARIO. Casi todos los sistemas digitales utilizan el sistema numérico binario (base 2), debido a que es más fácil diseñar circuitos electrónicos sencillos y precisos que operen con sólo dos niveles de voltaje.
En el sistema binario sólo hay dos símbolos o posibles valores de dígitos, 0 y 1. No obstante, este sistema de base 2 se puede utilizar para representar cualquier cantidad que se denote en sistema decimal o cualquier otro sistema numérico.
En este sistema, el término dígito binario se abrevia a menudo como bit. En la representación el bit más significativo (MSB) es aquel que se ubica más a la izquierda del punto binario, que representan la parte fraccionaria. El bit menos significativo (LSB)es aquel que está más a la derecha y que tiene menor valor.
REPRESENTACIÓN DE CANTIDADES BINARIAS
En los sistemas digitales la información que se esta procesando por lo general se presenta en forma binaria. Las cantidades binarias pueden representarse por medio de cualquier dispositivo que solamente tenga dos estados de operación o posibles condiciones. Por ejemplo, un interruptor sólo tiene dos estados: abierto o cerrado. Arbitrariamente, podemos hacer que un interruptor abierto represente el cero binario y que uno cerrado represente el 1 binario. Otros dispositivos pueden operar en dos condiciones, el foco puede estar encendido o apagado, el diodo, activado o desactivado, el relevador, energizado o desenergizado; y muchos otros.
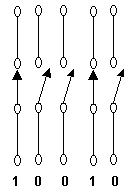
Uso de interruptores
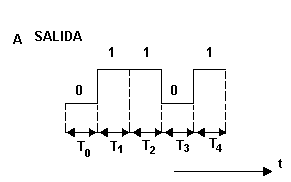
Otra diferencia entre los sistemas digitales y los analógicos es que en los sistemas digitales, el valor exacto de un voltaje no es importante; por ejemplo, un voltaje de 3.6 V es igual que uno de 4.3 V. En los sistemas analógicos, el valor exacto de un voltaje si es importante.
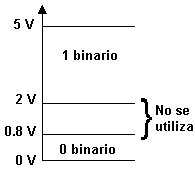
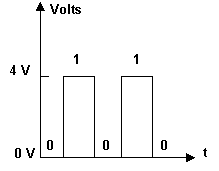
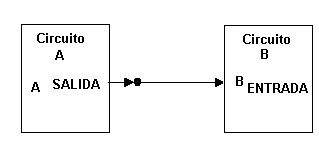
(a) (b)
(a) Asignaciones comunes de voltaje en el sistema digital; (b) señal digital común.
CIRCUITOS DIGITALES INTEGRADOS. Casi todos los circuitos que se utilizan en los sistemas digitales modernos son circuitos integrados (CI). Se utilizan diferentes tecnologías de fabricación de circuitos integraos para producir CI digitales; siendo los más comunes TTL, CMOS, NMOS y ECL. Cada uno difiere en el tipo de circuitos que se emplean para efectuar la operación lógica que desee. La tecnología TTL(lógica de transistor-transistor) se vale del transistor bipolar como elemento principal del circuito, en tanto que la CMOS (semiconductor metal óxido complementario) utiliza el transistor MOSFET como elemento principal del circuito.
TRANSMISIÓN PARALELA Y SERIAL
Una de las operaciones más comunes que se presentan en cualquier sistema digital es la transmisión de información de un lugar a otro. La información puede transmitirse a una distancia mínima de algunos milímetros sobre la misma tarjeta de circuito , o a varios kilómetros cuando el operador de una terminal de computadora se comunica con una computadora que esta en otra ciudad. La información que se transmite se encuentra en forma binaria y, por lo general, está representada por varios voltajes que aparecen en las salidas del circuito de transmisión que está representada por los voltajes que aparecen en las salidas del circuito de transmisión que están conectadas a las entradas del circuito de recepción. Hay dos métodos básicos empleados para la transmisión de información digital: el paralelo y el serial.
La transmisión paralela utiliza una línea por bit , y todos se transmiten en forma simultánea; (b) la transmisión serial emplea sólo una línea de señal; cada bit se transmite en forma consecutiva (uno por uno).
Así, la representación paralela es más rápida y la serial requiere menos líneas de señal.
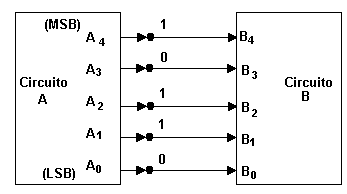
Transmisión paralela
Transmisión serial
CONVERSIONES DE BINARIO A DECIMAL
Como ya vimos el sistema de numeración binario es un sistema posicional donde cada dígito binario (bit) tiene un valor basado en su posición relativa al LSB. Cualquier número binario puede convertirse a su equivalente decimal, simplemente sumando en el número binario las diversas posiciones que contenga un 1.
Ejemplo 1.
1 1 0 1 12 (binario)
24 + 23 + 0 + 21 + 20 = 16+8+2+1
= 2710 (decimal)
Ejemplo 2.
1 0 1 1 0 1 0 12 =
27 + 0 + 25 + 24 + 0 + 22 + 0 + 20 =
128+ 0 + 32 + 16 + 0 + 4 + 0 + 1 = 18110
CONVERSIONES DE DECIMAL A BINARIO
Existen dos maneras de convertir un número decimal entero a su representación equivalente en el sistema binario. El primer método es inverso al proceso descrito en la sección anterior. El número decimal se expresa simplemente como una suma de potencias de 2 y luego los unos y los ceros se escriben en las posiciones adecuadas de los bits.
Ejemplo 1.
4510 = 32 + 8 + 4 + 1 = 25 + 0 + 23 + 22 + 0 + 20
= 1 0 1 1 0 121
Obsérvese que se coloca un cero en las posiciones 21 y 24, ya que todas las posiciones deben tomarse en cuenta.
Ejemplo 2.
7610 = 64 + 8 + 4 = 26 + 0 + 0 + 23 + 22 + 0 + 0
= 1 0 0 1 1 0 02
Otro método emplea la división repetida por 2. La conversión, que se ilustra a continuación para 2510 requiere dividir repetidamente el número decimal entre 2 y que se escriban los residuos después de cada división hasta que se obtenga un cociente de cero. Nótese que el resultado binario se obtiene al escribir el primer residuo como el LSB y el último como MSB.
Ejemplo1.
2510
25/2 = 12 + residuo de 1
12/2 = 6 + residuo de 0
6/2 = 3 + residuo de 0
3/2 = 1 + residuo de 1
1/2 = 0 + residuo de 1
MSB
2510 = 1 1 0 0 12
LSB
2510 = 110012
Ejemplo 2.
3710 =
37/2 =18.5 residuo de 1 (LSB)
18/2 =9.0 residuo de 0
9/2 =4.5 residuo de 1
4/2 =2.0 residuo de 0
2/2 =1.0 residuo de 0
1/2 =0.5 residuo de 1 (MSB)
Por tanto, 3710 = 1001012
CONVERSIONES DE DECIMALES
Para convertir decimales se multiplicara por 2 repetidamente el número decimal y que se escriban los residuos después de cada multiplicación tomando como residuo la cantidad a la izquierda del punto hasta que se obtenga un resultado de 1. El resultado binario se obtendrá al escribir el primer residuo como el MSB y el último como LSB, es decir, se tomara al revés.
Ejemplo 1.
Convertir a binario
(0.6875)10
0.6875*2 = 1.375 residuo de 1 (MSB) (0.6875)10 =(0.1011)2
0.375*2 = 0.75 residuo de 0
0.75*2 = 1.5 residuo de 1
0.5*2 = 1.0 residuo de 1 (LSB)
Para convertir binario a decimal se toma la cantidad a la izquierda del punto y se convierte a decimal como ya se ha visto. Después se tomara la cantidad a la derecha del punto, y se comenzara desde la última elevando el 2-1 y la siguiente 2-2, así sucesivamente hasta llegar al punto. Después se toman las dos cantidades y se suman.
Ejemplo 2.
Convertir a decimal (1111.1111)2
1 1 1 1 . 1 1 1 1
23 22 21 20 = 8+4+2+1 = 15 2-4 2-3 2-2 2-1
=0.5+0.25+0.125+0.0625 = .9375
15+.9375= 15.9375
SISTEMA DE NUMERACIÓN HEXADECIMAL
El sistema hexadecimal emplea la base 16. Así tiene 16 posibles símbolos digitales. Utiliza los dígitos del 0 al 9 más las letras A, B, C, D, E y F como sus símbolos digitales. Los dígitos hex (abreviatura de hexadecimal) de A aF son equivalentes a los valores decimales de 10 a 15.
Tabla de las relaciones entre los sistemas hexadecimal, decimal y binario.
| Hexadecimal | Decimal | Binario |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
CONVERSIÓN DE HEXADECIMAL A DECIMAL
Un número hex se puede convertir a su equivalencia decimal utilizando el hecho de cada posición de los dígitos hex tiene un valor que es una potencia de 16. El LSD tiene un valor de 160 =1; el siguiente dígito en secuencia tiene un valor de 161=16; el siguiente tiene un valor de 162=256 y así sucesivamente. El proceso de conversión se demuestra en los siguientes ejemplos.
Ejemplo 1.
Convertir a decimal
35616 = 3*162 +5*161 +6*160
= 768 + 80 + 6
= 85410
Ejemplo 2.
Convertir a decimal
2AF16 = 2* 162 + 10*161 + 15*1601
= 512 + 160 + 15
= 68710
CONVERSIÓN DE DECIMAL A HEXADECIMAL
La conversión de decimal a hexadecimal se puede efectuar por medio de la división repetida entre 16.
Ejemplo 1.
Convierte 42310 a hexadecimal
423/16 =26 + residuo de 7
26/16 =1 + residuo de 10
1/16 =0 + residuo de 1
42310 = 1A716
Ejemplo 2.
Convierte 21410 a hexadecimal
214/16 =13 + residuo de 6
13/16 =0 + residuo de 13
21410 = D616
CONVERSIÓN DE HEXADECIMAL A BINARIO
Cada dígito hexadecimal se convierte en su equivalente binario de 4 bits.
Ejemplo 1.
Convertir 9F216 a binario
9F216 = 9 F 2
1001 1111 0010
= 1001111100102
CONVERSIÓN DE BINARIO A HEXADECIMAL
Esta conversión es exactamente la operación inversa del proceso anterior. El número binario se agrupa en conjunto de 4 bits y cada grupo se convierte a su dígito hexadecimal equivalente. Cuando es necesario se añaden ceros para completar un grupo de 4 bits.
Ejemplo 1.
Convertir 11101001102 a hexadecimal
11101001102 = 0011 1010 0110
3 A 6
= 3A616
COMPUERTAS
AND NAND
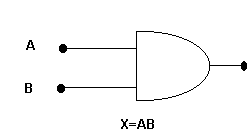
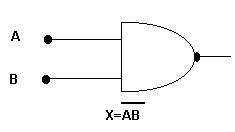
| AND | NAND | ||
| A | B | X=AB | X´=AB |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
OR NOR
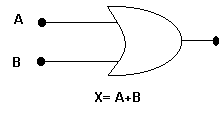
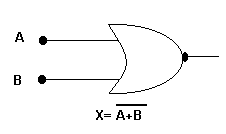
| OR | NOR | ||
| A | B | X=A+B | X´=A+B |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
NOT SEGUIDOR O BUFFER


Hace que no decaiga la corriente
| A | X=A |
| 1 | 1 |
| 0 | 0 |
| A | X=A' |
| 1 | 0 |
| 0 | 1 |
AND OR
TRANSISTOR
El 0 y el 1 representan el estado de una variable de voltaje o bien lo que se conoce como su nivel lógico. También se emplean otros sinónimos como los de la siguiente tabla.
| 0 LÓGICO | 1 LÓGICO |
| Falso Desactivado Bajo No Interruptor Abierto | Verdadero Activado Alto Si Interruptor Cerrado |
Tabla de verdad para tres entradas con diferentes operaciones
| A | B | C | OR | NOR | AND | NAND |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 |
TEOREMAS DE BOOLE
Postulado 2 (a) x+0=x (b) x.1= x
Postulado 5 (a) x+x'=1 (b) x.x'= 0
Teorema 1 (a) x+x=x (b) x.x= x
Teorema 2 (a) x+1=1 (b) x.0=0
Teorema 3, involución (x')'=x
Postulado 3, conmutativo (a) x+y= y+x (b) xy=yx
Teorema 4, asociativo (a) x+(y+z)=(x+y)+z (b) x(yx)=(xy)z
Postulado 4, distributivo (a) x(y+z)=xy+xz (b) x+yz=(x+y)(x+z)
Teorema 5, De Morgan (a) (x+y)'=x'y' (b) (xy)'=x'+y'
Teorema 6, absorción (a) x+xy=x (b) x(x+y)=x
Teorema 1(a): x+x=x
x+x=(x+x).1 del postulado: 2(b)
=(x+x).(x+x') 5(a)
=x+xx' 4(b)
=x+0 5(b)
=x 2(a)
Teorema 1(b): x.x=x
x.x=xx+0 del postulado: 2(a)
=xx+xx' 5(b) =x(x+x') 4(a)
=x.1 5(a)
=x 2(b)
Nótese que el teorema 1(b) es el dual del teorema 1(a) y que cada paso de la prueba en parte (b) es el dual de la parte (a). Cualquier teorema dual puede derivarse similarmente de la prueba de un par correspondiente.
Teorema 2(a): x+1=1
X+1=1.(x+1) del postulado: 2(b)
=(x+x')(x+1) 5(a) =x+x'.1 4(b)
=x+x' 2(b)
=1 5(a)
Teorema 2(b): x.0=0 por dualidad
Teorema 3: (x')'=x Del postulado 5, se tiene x+x'=1 y x.x'=0, lo cual define el complemento de x. El complemento de x' es x y es también (x')'. Así como el complemento es único tendremos que (x')=x.
Los teoremas que comprenden dos o tres variables pueden ser probados algebraicamente de los postulados y de los teoremas ya probados. Tómese por ejemplo el teorema de absorción.
Teorema 6(a): x+xy=x
x+xy=x.1+xy del postulado: 2(b)
=x(1+y) 4(a) =x(y+1) 3(a)
=x.1 del teorema 2(a)
=x del postulado 2(b)
Teorema 6(b): x(x+y)=x por dualidad
FUNCIONES
X= ABC+BC+AC (Como es una compuerta AND se multiplica)
1
Diagrama de Ven
F1= x+xy=x F2= x.x=x
X'

F1= x(y+z)= xy+xz

MAPAS DE KARNAUGH
PRACTICAS
Display de 7 segmentos
GLOSARIO
BCD. Código Binario Decimal.
LSB. (Low Significal Bit). Bit menos significativo
MSB(More Significal Bit) .Bit más significativo.
Compuerta AND.
Compuerta NAND.
Compuerta OR.
Compuerta NOR.
BIBLIOGRAFÍA
SISTEMAS DIGITALES
PRINCIPIOS Y APLICACIONES
RONALD J. TOCCI
PRENTICE HALL
X
b
a
c
d
e
f
g
Descargar
| Enviado por: | Ara |
| Idioma: | castellano |
| País: | México |
