Comunicación Audiovisual
Sistemas de Video
Práctica 1: Tratamiento básico y conversión de ficheros gráficos.
Introducción.
En esta práctica se desarrollan algunos aspectos básicos del tratamiento de imágenes con el objetivo de familiarizar al lector con algunas de las herramientas software que se utilizaran durante el curso. La mayor parte de los conceptos se presentan utilizando el 'Notebook' de Matlab, donde se sugieren las rutinas a utilizar y se presentan algunas ideas para que el alumno desarrolle directamente, como ejercicio, algunos programas en la ventana de comandos de Matlab. Pretendemos que al final de esta sesión el estudiante pueda desarrollar de forma autónoma la carga y evaluación de algoritmos simples sobre las imágenes y conozca los aspectos más significativos de los formatos de imagen con los que trabajaremos a lo largo del curso.
Los aspectos que consideraremos durante la ejecución de esta práctica son:
Lectura y carga de ficheros bitmap desde el Notebook y desde el editor de comandos del Matlab.
Representación de los ficheros en ventanas gráficas.
Análisis del contenido de los ficheros en las matrices que representan la imagen.
Conversión entre formatos tipo byte y formatos de coma flotante para el tratamiento de la imagen.
Cálculos de luminancia y componentes diferencia de color. Conversión entre componentes rgb y componentes yuv. Formato ITU-601 y ventajas de las componentes yuv.
Negativos, binarización y filtrados paso alto y paso bajo de imágenes.
Conversión de formato bitmap a formato *.lum.
Conversión de formato bitmap a formato *.yuv.
Carga de ficheros Bitmap en el entorno Matlab y Notebook.
Durante la ejecución de esta práctica supondremos que todas las imágenes y rutinas del matlab están almacenados en el directorio 'c:\practica1'. Para ello es necesario crear y copiar todos los ficheros asociados a esta práctica a un directorio con este nombre. La definición del directorio dentro de nuestro entorno requiere ejecutar la instrucción:
cd 'c:\practica1';
Para cargar un fichero de tipo bitmap en el entorno Matlab basta con realizar la siguiente sentencia (suponemos que la imagen que deseamos cargar esta disponible en el directorio):
imbn = imread('senyorabn.bmp');
La imagen está cargada en la variable imbn, puede visualizarse ejecutando la sentencia:
imshow(imbn);
Todas las sentencias ejecutadas hasta este momento podrían haberse ejecutado directamente desde la ventana de comandos del Matlab. Como prueba, maximice la ventana Matlab Command Window y ejecute la siguiente secuencia de sentencias:
imbn2 = imread('senyorbn.jpg');
imshow(imbn2);
Las sentencias también podrían haberse ejecutado directamente desde el Notebook:
imbn2=imread('senyorbn.jpg'); imshow(imbn2);
En este segundo ejemplo, hemos cargado en la variable imbn2 una imagen que originalmente tenía el formato JPEG. La rutina imread permite cargar los formatos de imágenes más habituales. Puede ver los detalles de esta función del Matlab, situándose en la ventana de comandos y ejecutando la sentencia help imread. Esta rutina, admite distintos parámetros de entrada y salida, en función de las características de la imagen y del formato con el que deseemos representarla dentro del Matlab. En nuestro caso, sólo estámos interesados en un uso básico de la rutina como el que se ha descrito en los apartados anteriores.
Debe notarse que, independientemente del tipo de formato con el que estén almacenados los datos (*.bmp; *.jpg), las imágenes se representan como matrices. En el caso de imágenes en blanco y negro, cada elemento de la matriz representa el nivel de gris de la imagen. El tamaño de la matriz puede determinarse ejecutando la instrucción size(imbn2), lo que devuelve el número de filas y de columnas de la imagen. Esta instrucción puede ejecutarse directamente desde el interprete de comandos o desde el Notebook.
size(imbn)
ans =
288 384
size(imbn2)
ans =
308 344
Obsérvese que para obtener una respuesta del Matlab, las sentencias deben finalizarse sin el punto y coma.
Podemos ver el valor de un elemento de imagen referenciándo la variable que la representa como una matriz. Así, para ver el nivel de gris del pixel situado en la fila 27, columna 32 de la imagen ejecutaríamos la sentencia:
imbn(27,32)
ans =
141
Este valor también puede asignarse a una variable:
Pixel = imbn(27,32);
o incluso a una matriz con otras dimensiones:
imaux = imbn(1:150,1:150);
donde ahora, podemos examinar la variable imaux y comprobar sus dimensiones:
size(imaux)
ans =
150 150
Si visualizamos la imagen obtenemos:
imshow(imaux);
lo que indica que imaux es una subimagen formada por las 150 primeras filas y columnas de la imagen original.
A la vista de estos resultados, ejecute las siguientes sentencias, desde este Notebook:
imaux1 = imbn(100:188,150:384);
imaux2 = imbn(1:2:288,1:2:384);
Cuestiones:
Examinando los tamaños de las imágenes 'imaux1' e 'imaux2' y viendo sus representaciones gráficas, indique que tipo de operaciones se han realizado en los dos sentencias anteriores. El examen de las dimensiones y la visualización de las imágenes puede realizarlo directamente desde la ventana de interprete de comandos de Matlab o utilizando las siguientes sentencias desde el Notebook.
size(imaux1)
ans =
89 235
size(imaux2)
ans =
144 192
imshow(imaux1);
imshow(imaux2);
RESPUESTA: Lo que observamos es por una parte una sección de la imagen, o sea en este primer caso la operación que hemos realizado es recortar la imagen convirtiéndola en una matriz de 89 por 235 pixeles, su matriz inicial era de 288 por 384 pixeles, y dicho resultado es el que vemos en la variable imaux1, a través de la sentencia imshow(imaux1).
En la imaux2 lo que ha sucedido con la instrucción "imaux2 = imbn(1:2:288,1:2:384);" es que han sido eliminados todos los pixeles pares, o sea que nuestra imagen se ha vuelto 4 veces más pequeña, que la original, obteniendo también una perdida considerable de resolución.
Así mismo hemos creado con dicha sentencia una matriz formada por la columna desde el pixel 1 hasta 384, y las filas desde el pixel 1 hasta el 288. Aunque después de ejecutar la instrucción se nos quede en 144 filas y 192 columnas.
Indique que operación realizaría para obtener una imagen de 100x100 píxeles situáda en la parte central y que tuviera la misma resolución que la imagen original.
RESPUESTA:
La operación que necesitaríamos para obtener una imagen de 100 x 100 pixeles y situada en la parte central seria la siguiente:
[size(imaux2)]
-
ans =
-
144 192
[imbn(94,142)]
ans =
216
Pixel = imbn (94,142);
imaux2 = imbn(94:194,142:242);
[imshow(imaux2); ]
ans =
2.0007
Nuestra imaux2 ahora sera una imagen compuesta entre 94 y 194 pixels por fila, y por 142 y 242 pixels por columna, ésta formada de 100 filas y de 100 columnas, y con la misma resolución y calidad que la original ya que no hemos descartado ninguna fila ni columna, (par o impar), y de esta manera obtenemos nuestra matriz deseada.
Tratamiento numérico de las imágenes en blanco y negro.
El formato numérico con el que se representan las imágenes anteriores en el Matlab es el uint8 (unsigned integer 8 bits). Se trata de un formato muy eficiente en el que el nivel de gris de cada elemento de imagen se representa únicamente con 8 bits, representando los números desde el 0 hasta el 255. No obstante, este formato no resulta adecuado para realizar operaciones sobre los elementos de imagen por cuanto no es posible asegurar que después de las mismas los niveles de gris de la imagen se sigan manteniendo en el margen 0, .., 255. Existen dos posibles alternativas para realizar de forma eficiente el procesado de las imágenes. La primera consiste en convertir los niveles de gris de la imagen a números reales que están situados entre 0 y 1, lo que se conoce como intensity image. Ahora, el nivel 0 corresponderá al negro mientras que el nivel 1 representará el blanco. El resto de valores representarán distintos gradaciones de nivel de gris. La conversión a una imagen de intensidad puede realizarse mediante una única sentencia:
imbnint = double(imbn)/255;
El operador double actúa sobre la imagen imbn convirtiendo todos los valores uint8 a números en coma flotante. Posteriormente, cada uno de los números de la matriz se divide por 255 asignándose a la matriz resultante imbnint. Debe observarse que el Matlab es un lenguaje matricial de muy alto nivel que interpreta las sentencias en función del contenido de las variables. Esto significa que en una única sentencia hemos realizado la asignación de una matriz completa a otra matriz. En lenguajes de más bajo nivel, como el C++ o el Visual Basic, deberíamos haber realizado la asignación de cada uno de los elementos por separado mediante el uso de dos bucles tal y como se ilustra en el siguiente algoritmo:
for i = 1:288;
for j = 1:384;
imbnint(i,j) = double(imbn(i,j))/255.;
end;
end;
Cuando la variable es un escalar (como la variable Pixel definida anteriormente), la sentencia anterior se realizaría a nivel de variable. Pruebe, como ejemplo, la siguiente sentencia:
Pixel2 = double(Pixel)/255
Pixel2 =
0.8471
Compruebe que el resultado obtenido coincide con el valor del elemento de imagen de la matriz imbnint en la fila 27, columna 32:
imbnint(27,32)
ans =
0.5529
La rutina imshow analizada anteriormente también interpreta de forma automática el formato de representación de la imagen. Así, cuando ejecutamos:
imshow(imbnint);
Identifica que la imagen está representada como niveles de intensidad y la representa en la pantalla. Realizaremos a continuación algunas operaciones básicas sobre la imagen. Para ello serán de utilidad las funciones max y min que proporcionan los valores máximos y mínimos de la imagen. Ejecute:
max(max(imbnint))
ans =
0.9608
min(min(imbnint))
ans =
0.0039
La función max aplicada a una matriz devuelve un vector fila cuyos elementos son el valor máximo de cada una de las columnas de la matriz. Para comprobar el significado de esta operación genere la matriz A siguiente y compruebe el resultado del operador max()
A = [1 7 2; 4 9 6; 10 6 3]
A =
1 7 2
4 9 6
10 6 3
max(A)
ans =
10 9 6
Si aplicamos el operador max sobre un vector fila o columna el resultado es directamente el elemento de mayor valor. Por tanto, el resultado de aplicar max(max(A)) proporcionará el valor máximo de la matriz. El operador min se comporta de forma análoga pero determinando el mínimo de la matriz o del vector.
Realizaremos distintas operaciones elementales. En primer lugar, reduciremos el nivel de la luminancia:
im1 = 0.5*imbnint;
Esta operación divide por 2 el nivel de gris de todos los elementos de la imagen. Por tanto, la observaremos más oscura.
imshow(im1);
Nota: La imagen resultante, es algo mas oscura que la original, ya como se ha comentado anteriormente los tonos grises han sido divididos por dos.
Ahora, sumaremos una constante a todos los elementos de la imagen, lo que es equivalente a aumentar el brillo en un receptor de TV.
im1 = im1+1;
Nota:Nuestra protagonista ha oscurecido, logicamente gracias a la suma de dicha constante.
Esta instrucción suma la unidad a todos los elementos de la imagen. Por ello, es posible que el margen de valores de im1 ya no esté comprendido entre los límites 0,..,1 que exige la representación de la imagen como niveles de intensidad. Para ello, la reescalamos antes de visualizarla:
im1 = im1/max(max(im1)); imshow(im1);
Nota: La imagen es mas blanca, han desaparecido los tonos oscuros, éstos se han convertido en grisaceos, y los grisaceos en blancos, asemejando la imagen original.
Ahora realizaremos una mejora de contraste de la imagen resultante. Para ello, en primer lugar, calculamos su valor medio y lo sustraemos de la imagen. A partir de los valores máximos y minimos del resultado realizamos una transformación que ajuste el valor mínimo al negro y el máximo al blanco:
im2 = im1-mean(mean(im1)); a = max(max(im2)); b=min(min(im2));
im2 = (im2-b)*(1/(a-b)); imshow(im2);
Nota: La imagen ha recuperado su brillo, su saturacion, en definitiva se han restaurado sus tonos originales.
Cuestiones.
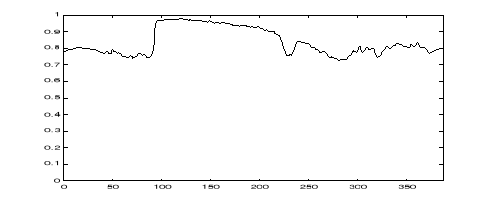
Justifique las operaciones realizadas en el apartado anterior para mejorar el contraste. Interprete el método utilizado ayudándose de una señal que represente el nivel de gris en una de las líneas de la imagen. (Nota: Tome como ejemplo el nivel de gris en la línea 100 en la imagen im1, que se representa en la figura siguiente).
RESPUESTA: La metodologia que hemos seguido es lograr que las frequancias altas, sean las maximas, y las frequencias bajas sean las minimas. O sea que calculamos el valor medio de la imagen im1, a im1 le damos el valor im2, y con la siguiente sentencia:
im2 =im1-mean (mean(im1)) lo que hacemos es calcular el valor medio de los pixels de la imagen.
Con la instrucción im2= (im2-b)*(1/(a-b)) lo que hacemos convertir todos los valores de la imagen a numeros reales situados entre 0 y 1, tomando como a 1 blanco y como a 0 negro, o ausencia de color o lo que literalmente se denomina Intensy image.
Utilizando la función 'plot' del Matlab y la ayuda reproduzca la gráfica de la figura proporcionada en el ejercicio anterior. Realice las pruebas directamente en la ventana de comandos del Matlab e indique las sentencias utilizadas para obtener la representación.
RESPUESTA:
Como hemos visto, las instrucciones utilizadas son plot, logicamente.
o sea plot ( im2 ( 100,1:384 ), axis([1,384,0,1]);
Indique que operaciones utilizaría para representar el negativo de una imagen.
RESPUESTA: im-neg = 1- im2
variable = 1-im2;
imshow (variable)
Realización de rutinas y funciones en Matlab.
En esta sección revisaremos algunos conceptos básicos para trabajar en la ventana de comandos de Matlab y aprenderemos los principios para realizar rutinas y funciones que agrupen una secuencia de instrucciones. La mayor parte de las sentencias que revisaremos se utilizan de forma habitual y pueden usarse tanto desde la ventana de comandos como desde el Notebook. Sin duda, el recurso más utilizado del Matlab es la instrucción help. Puede ejecutarse directamente desde la ventana de comandos para proporcionar ayuda en línea sobre una instrucción o bien recurrir a una ayuda interactiva de tipo texto o, en el modo más avanzado, acceder a los ficheros html desde un navegador donde pueden obtenerse los manuales completos y un sistema de búsqueda avanzado.
Otra instrucción utilizada con frecuencia es who, que indica las variables que están activas en la ventana actual. Si ejecuta la instrucción who desde la ventana de comando verá listadas todas las variables que hemos ido creando durante la ejecución de esta práctica.
Las instrucciones load y save también son muy usadas. La instrucción save almacena en disco todas las variables del entorno de trabajo mientras que la función load las recupera del disco. Cuando se trabaja con el Notebook es útil guardar de vez en cuando las variables del entorno de trabajo por si se cierra accidentalmente el Matlab. En este caso, podrá continuarse con la ejecución interactiva del Notebook desde el último punto donde se haya realizado el save. Las variables se salvan y se recuperan por defecto del fichero Matlab.mat. Puede especificarse cualquier otro nombre de fichero.
La función uigetfile se utiliza para invocar una interficie gráfica de windows que permita adquirir el nombre de un fichero y el directorio en el que está localizado. Pruebe de ejecutar la siguiente instrucción desde la interficie de comandos:
[nom,path] = uigetfile('*.bmp');
Compruebe los valores de las variables nom y path (para ver los valores desde la ventana de comandos basta con teclear el nombre de la variable sin punto y coma final y pulsar la tecla return).
Veremos ahora como generar un fichero tipo texto que ejecute una secuencia de operaciones con una única instrucción. Para ello, siga los pasos siguientes:
-
Desde la ventana de comandos seleccione el menú File, opción New, M-File.
-
Escriba en el fichero las sentencias que desea ejecutar:
[name,path]=uigetfile('*.bmp');
imag = imread([path,name]);
-
Guardar el fichero con el nombre lee_imag.m en el directorio de trabajo de la práctica_1 y cerrar el editor de texto.
Ahora puede ejecutar la sentencia lee_imag desde la ventana de comandos del Matlab con lo que se cargará la imagen seleccionada en la variable imag. La nueva instrucción también es accesible desde el Notebook. Para probarlo puede eliminar la variable imag, actualmente en la memoria, ejecutando la instrucción clear imag. Compruebe ejecutando la orden who que la variable ha desaparecido del entorno de trabajo y ejecute la siguiente instrucción desde este M-book.
lee_imag;imshow(imag);
Compruebe que la variable imag vuelve a estar definida en el entorno de trabajo. La generación de ficheros del tipo *.m es muy útil pues permite agrupar sentencias que se realizan de forma sistemática en una única instrucción. Los ficheros se ejecutan invocando la rutina con el nombre del fichero y los resultados obtenidos son equivalentes a la ejecución de todas las instrucciones individuales desde la ventana de comandos. Todas las variables que hayan sido definidas en el fichero *.m son ahora accesibles desde el entorno de trabajo.
De forma parecida, pueden definirse nuevas funciones, con la ventaja de que las variables internas serán locales y por tanto no serán accesibles una vez ejecutada la función. Definiremos una función que realice la carga automática de un fichero. Para ello, desde la ventana de comandos genere un nuevo fichero M-file y escriba las siguientes instrucciones:
function [imag] = lee_imagen();
[name,dir]=uigetfile('*.bmp');
imag = imread([dir,name]);
return
Guarde el fichero con el mismo nombre que la función. Ahora puede ejecutar la instrucción asignándo el resultado de la lectura a cualquier variable tanto desde la interficie de comandos como desde el M-book:
lee_imagenNUEVA= lee_imagen;imshow(c);
Filtrado de imágenes.
En esta sección veremos algunos ejemplos de filtrado de imágenes mediante plantillas que nos servirán tanto como una revisión de conceptos básicos ya estudiados en el curso anterior como para una primera aproximación a la transformada Wavelet, cuyos detalles serán analizados en una práctica posterior.
Consideremos la plantilla siguiente:
P = (1/9)*ones(3,3);
Se trata de una plantilla de valor promedio en el que cada pixel de la imagen resultante se obtiene como el valor medio entre los pixeles situados en un entorno 3x3 sobre el pixel que se está calculando. El resultado de filtrar la imagen imbnint mediante esta plantilla puede obtenerse utilizando la instrucción filter2. Así, el resultado de la imagen filtrada será:
im9 = filter2(P,imbnint);imshow(im9);
Podemos comparar la imagen original con la resultante del filtrado paso bajo, representando ámbas en la misma figura:
subplot(121);imshow(imbnint);subplot(122);imshow(im9);
Evidentemente, si se aumenta el tamaño de la plantilla promedio, el efecto del filtrado paso bajo es más pronunciado:
P25 = (1/25)*ones(5,5); P49 = (1/49)*ones(7,7); im25 = filter2(P25,imbnint);im49 = filter2(P49,imbnint);
Ahora podemos comparar en una misma gráfica todos los resultados:
subplot(221);imshow(imbnint);subplot(222);imshow(im9); subplot(223);imshow(im25); subplot(224);imshow(im49);
La diferencia entre la imagen original y una imagen paso bajo puede considerarse como un filtrado paso alto puesto que se cancelan las componentes de baja frecuencia manteniéndose únicamente las de alta frecuencia. Consideremos la resta de las dos imágenes:
imdif = imbnint-im25;
La imagen diferencia puede tomar tanto valores positivos como negativos por lo que no es posible representarla directamente en el margen de niveles de luminancia entre el negro y el blanco. Existen dos alternativas para su representación. La primera consiste en representar el valor absoluto:
imshow(abs(imdif));
El problema de esta representación es que las diferencias entre las imágenes tienen un valor absoluto muy pequeño por lo que su apariencia global es totalmente oscura. Puede mejorarse la representación si se escala la visualización a todo el margen dinámico.
imshow(abs(imdif)/max(max(abs(imdif))));
En este caso, las diferencias más importantes se concentran en los márgenes de la imagen diferencia, donde el filtrado es ambiguo debido a los contornos de la imagen. Si normalizamos únicamente la zona central de la imagen obtendríamos:
imdif2 = imdif(11:278,11:374); imshow(abs(imdif2)/max(max(abs(imdif2))));
Otra alternativa, consiste en multiplicar el valor absoluto por un escalar fijo, siempre que no superemos los límites entre 0 y 1 de la luminancia:
imshow(5*abs(imdif2));
Otra opción, para representar imágenes diferencia o los resultados de un filtro paso alto consiste en sumar un valor de continua constante a toda la imagen. Con ello, los valores centrados en el origen (diferencias nulas) quedarán ahora centrados en el nivel gris medio mientras que los valores positivos tenderán hacia el blanco y los negativos hacia el negro. Esta es la forma con la que habitualmente se representan los filtrados obtenidos a partir de la transformada Wavelet. En nuestro caso tendríamos:
imshow(imdif2+0.5);
O directamente sobre la imagen original:
imshow(imdif+0.5);
CUESTIONES:
Indique porqué no es necesario reescalar la imagen resultante de los filtros de promedio.
RESPUESTA: No es necesario reescalar , ya que solo disponemos de pixels comprendidos entre 0 y 1.
Proponga una plantilla que aplicada directamente a la imagen imbnint se obtuviera la imagen imdif con la que hemos estado trabajando. Compruebe que los resultados obtenidos con la plantilla propuesta son exactos.
RESPUESTA: Tenemos que definir una nueva matrix, o sea una nueva plantilla que seria:
Plantilla = -(1/25)*ones(5,5)
Realice una rutina, basándose en bucle 'for', que implemente la misma función que filter2. Llame a la rutina filterp e incluyala como un fichero *.m.
RESPUESTA: (Código de la rutina)
Antes de continuar liberaremos la memoria del entorno de trabajo del Matlab y cargaremos una nueva imagen:
clear all; imag = imread('c:\practica1\senyorbn.jpg');
Normalizamos la imagen obtenida al dominio 0,1:
imag = double(imag)/max(max(double(imag)));
Otras plantillas de uso habitual para el análisis de contornos de las imágenes son los estimadores de gradiente o de derivadas direccionales. Uno de los más utilizados para la estimación de la derivada en el sentido horizontal es:
Ph = [-1 0 1; -1 0 1; -1 0 1];
El resultado de aplicar esta plantilla a la imagen es:
imhor = filter2(Ph,imag);imshow(abs(imhor)/max(max(abs(imhor))));
Nótese que el resultado de tratamiento de la imagen resalta principalmente los contornos verticales. Es habitual aplicar una binarización de la imagen de manera que si el nivel de gris normalizado supera un determinado umbral los pixeles se representen como blancos mientras que si no superan este nivel se representan como negros. Una posible forma para binarizar la imagen es:
umbral = 0.1; imh = abs(imhor)/max(max(abs(imhor)));
imh =0.5*(sign(imh-umbral)+1); imshow(imh);
CUESTIONES
Pruebe distintos niveles de umbral hasta determinar un valor óptimo para detectar los contornos verticales de la imagen.
RESPUESTA:
El valor de umbral correcto es el de 0,06 ya que nos permite difereciar los conotrnos.
Ayudándose del help de Matlab, justifique porqué la función anterior realiza una binarización de la imagen.
RESPUESTA: La funcion sign nos da como resultado un 1 positivo si el valor analizado es mas grande que zero. Zero si es igual a zero, y -1, si el valor analizado es negativo. A partir de aquí obtenemos una imagen en la que los valores 1 son claros, los valores -1 son oscuros, y 0 son negros.
Ahora tenemos que tranformar los valores obtenidos, o sea para hacer que el valor -1 sea positivo lo que hacemos es sumar 1, y así sucesivamente hasta que llegemos a normalizar dicha función.
Para obtener una estimación de los contornos debemos girar la plantilla unos 90º. Una forma de realizar un giro de la matriz es la transposición (cambio de filas por columnas):
Pv = Ph';
imver = filter2(Pv,imag),imshow(abs(imver)/max(max(abs(imver))));
Análogamente al caso anterior podemos calcular el resultado de la binarización de esta imagen.
CUESTIONES
Calcule, desde la interficie de comandos del Matlab, una imagen imv que contenga los contornos verticales
Combine las dos imágenes imv y imh para obtener una representación tanto de los contornos verticales como de los horizontales.
Un método alternativo para determinar los contornos de la imagen lo proporciona el propio Matlab con la instrucción edge. En este caso, el cálculo del umbral lo realiza el Matlab de forma automática.
iw = edge(imag,'prewit');imshow(iw);
Otra forma habitual de obtener los contornos de la imagen consiste en utilizar el filtro de Sobel que es una variante del filtro de prewit que hemos considerado en éste apartado. La plantilla asociada al filtro de sobel para la estimación de gradientes horizontales es:
Phsobel = [-1 0 1; -sqrt(2) 0 sqrt(2); 1 0 1];
Los contornos que obtendríamos con el filtro de Sobel son:
iw = edge(imag,'sobel'); imshow(iw);
Consideraremos ahora, brevemente, la implementación de filtros bidimensionales a partir de filtros unidimensionales más simples. Considere la siguiente plantilla horizontal:
P1 = [-1 0 1]; i1 = filter2(P1,imag); imshow(i1+0.5);
donde ahora hemos elegido la representación respecto al nivel de gris medio en sustitución de la representación mediante el valor absoluto. P2 será ahora un filtro de promedio en la dirección vertical (obsérve que la matriz está traspuesta):
P2 = [1 1 1]'; i2 = filter2(P2,i1);imshow(i2+0.5);
Examinemos ahora el siguiente resultado:
imshow(imhor-i2+0.5);
CUESTIONES:
Podría justificar por qué la imagen resultante anterior es nula ?
RESPUESTA:Hemos cogido la imagen con contornos verticales y le hemos restado imhor. Pues hemos restado los valores de los contornos con la imatge nula. Entonces nos queda un fondo o sea un fondo con numeros negativos, como hemos explicado anteriormente, y, al sumar 0.5 se restablecen los tonos. O sea que en definitiva lo que hemos hecho es una superposición de filtros.
Como aplicación de la superposición de filtros vamos a considerar los resultados que se obtienen para dos filtros muy simples [1, 1] y [1, -1], aplicados a alternativamente en las direcciones horizontales y verticales. Las imágenes que se obtienen son una versión del primer nivel de la transformada Wavelet que consideraremos con detalles en prácticas posteriores.
PB=[1 1] ; PA = [1 -1];
imaux = filter2(PB,imag); im11 = filter2(PB',imaux/2); imshow(im11/2)
imaux = filter2(PB,imag); im12 = filter2(PA',imaux/2); imshow(im12+0.5)
imaux = filter2(PA,imag); im21 = filter2(PB',imaux/2); imshow(im21+0.5)
imaux = filter2(PA,imag);im22=filter2(PA',imaux/2);imshow(im22+0.5)
CUESTIONES.
Represente las 4 imágenes anteriores en una sola figura e interprete los resultados obtenidos.
RESPUESTA:
Representación de imágenes en color.
El procedimiento utilizado para la carga de las imágenes en color es idéntico al de blanco y negro:
clear all;
imag=imread('c:\practica_1\atletisme.bmp');
La visualización también es idéntica:
imshow(imag);
o bien, trabajando con imágenes de intensidad:
im = double(imag)/255; imshow(im);
No obstante, ahora la matriz asociada a la imagen se indexa con tres variables:
size(im)
Las dos primeras variables de la matriz se utilizan para referenciar, como en el caso de imágenes en blanco y negro, la fila y la columna. El tercer índice identifica la componente de color: 1 para el rojo, 2 para el verde y 3 para el azul. Así, para obtener las componentes RGB del elemento de imagen situado en la fila 27 columna 32:
Pixel = [imag(27,32,1);imag(27,32,2);imag(27,32,3)]
Los métodos matemáticos para el tratamiento de imágenes en color son, en la mayoría de las aplicaciones, idénticos a los utilizados para el blanco y negro aunque se aplican a las tres componentes simultáneamente por lo que aumenta considerablemente la carga computacional. Una alternativa, cuando sólo deseamos trabajar con la información de luminancia es convertir las imágenes de color en una imagen de blanco y negro que aporte la información de brillo. Esta conversión puede realizarse utilizando la ponderación visual de las tres componentes de color:
imbn = 0.3*im(:,:,1)+0.59*im(:,:,2)+0.11*im(:,:,3);imshow(imbn);
Puede comparar la información de cada una de las componentes con la imagen de color en una misma gráfica:
subplot(221);imshow(im);subplot(222);imshow(im(:,:,1));
subplot(223); imshow(im(:,:,2));subplot(224); imshow(im(:,:,3))
Observe como la camiseta roja y blanca de uno de los atletas aparece totalmente blanca en la componente roja mientras que aparece con las dos tonalidades en el resto de componentes.
También podemos comparar las tres componentes de color con la señal de luminancia en una misma gráfica:
subplot(221);imshow(imbn);subplot(222); imshow(im(:,:,1)); subplot(223); imshow(im(:,:,2));subplot(224);imshow(im(:,:,3))
Podríamos aplicar los procedimientos de detección de contornos únicamente a la imagen de luminancia, pues ésta ya contiene suficiente información para separar los objetos.
imcont = edge(imbn,'sobel',0.15);imshow(imcont);
Pruebe con distintos valores de la tercera variable para hacer más o menos sensible la binarización de la imagen.
La información de color también puede representarse mediante las componentes Y, U y V, tal y como se transmiten en el sistema PAL. Las componentes U y V pueden calcularse a partir de las componentes de color mediante la siguiente combinación lineal:
U = 0,493 (B-Y) = 0,493(-0.3R-0.59G+0.89B) = -0.147 R - 0.29 G + 0.438 B;
V = 0,877(R-Y) = 0,877(0.7 R -0.59 G -0.11B)= 0.61 R - 0.517 G - 0.096 B;
Por tanto, podemos calcular las componentes U y V de forma análoga a como hemos calculado la luminancia a partir de las componentes de color. Debe tenerse en cuenta en este caso, que el resultado de las operaciones puede producir elementos positivos y negativos. Por ello, las imágenes resultantes suelen representarse respecto a un nivel de gris medio. Del mismo modo, cuando las componentes u y v se almacenan en ficheros, suele sumarse 128 para que puedan ser representadas mediante 8 bits.
En el directorio de trabajo se dispone de la rutina bmp2yuv.m que ha sido generada para convertir imágenes en color del formato bmp a imágenes en formato *.yuv. Pruebe a utilizar esta rutina para distintos ficheros. La misma rutina convierte las imágenes a formato *.lum cuando las imágenes bitmap se presentan en blanco y negro. Realice también algunas pruebas con esta rutina. Utilice el programa 'Codec.exe' para comprobar que los ficheros obtenidos se abren correctamente (Tenga en cuenta que la mayoría de los programas de evaluación de códigos que presentaremos en esta asignatura sólo admiten estos formatos. Además, el tamaño de las imágenes para que los programas funciones correctamente debe ser CIF o QCIF).
CUESTIONES:
Edite el programa bmp2yuv.m y comente que operaciones se realizan y su objetivo en las distintas instrucciones.
RESPUESTA:
Modifique el programa bmp2yuv.m para que produzca una imagen en blanco y negro (en formato *.lum) a partir de un fichero bitmap en color. Llame bmp2lum a la nueva rutina.
RESPUESTA:
Descargar
| Enviado por: | Frederic Alvarez |
| Idioma: | castellano |
| País: | España |
