Ingeniero de Telecomunicación
Sistemas de Segundo Orden
PRACTICA 2
SISTEMAS DE SEGUNDO ORDEN
En la plantada montada en el laboratorio, se pretende medir con el módulo de adquisición SIGLAB, los siguientes parámetros:
Sobreimpulso máximo (Mp)
Tiempo de establecimiento (ts)
Tiempo de crecimiento (tr)
Tiempo de pico (tp)
Tiempo de retardo (td)
Se pretende hallar la función de transferencia
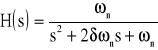
midiendo los parámetros “ts” y “Mp”. Se hará uso de las expresiones:
-
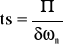
y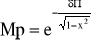
-
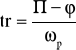
y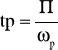
donde:
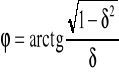
![]()
Posteriormente, se deberá hacer una simulación con la función de transferencia obtenida y comparar los resultados de dicha simulación con los medidos en el laboratorio.
Por último, se pretende hallar la respuesta en frecuencia (diagrama de Bode) de dicha planta, en “Simulink”.
Base teórica
Nos encontramos con un sistema de 2º orden cuya función de transferencia es:
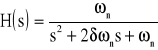
donde : ![]()
es el factor de amortiguamiento
![]()
es la pulsación angular o natural no amortiguada
La respuesta ante un escalón unitario puede ponerse de la siguiente forma:

La respuesta de un sistema de segundo orden se puede caracterizar en función del factor de amortiguamiento encontrándonos varios casos:
-

< 0 : Sistema inestable: En este sistema no tiene sentido hablar de factor de amortiguamiento. -

= 0 : Sistema no amortiguado: Sistema oscilatorio cuya respuesta es una senoide pura. -
0 <

< 1 : Sistema subamortiguado: La respuesta es un seo afectado por una exponencial. -

= 1 : Sistema crítico/amortiguado: No presenta oscilación -

> 1 : Sistema sobreamortiguado: Responde como un sistema de primer orden.
Vamos a ver ahora como es la respuesta en frecuencia de un sistema de segundo orden:
Tenemos que representar el módulo y la fase.
-
Módulo:

-
Fase:

Y lo representamos en sendas gráficas:
Módulo
Tiene dos diferencias significativas con respecto al sistema de primer orden:
-
Caída de 40 dB en vez de 20 dB como en el sistema de primer orden.
-
Este puede sobrepasar los 0 dB mientras que el de primer orden no.
Fase
Tiene dos diferencias significativas con respecto al sistema de primer orden:
-
Altas frecuencias (180º)
-
La frecuencia natural en vez de 90º son 45º.
Con respecto a las especificaciones en el tiempo tenemos:
-
Tiempo de retardo: Lo que tarda el sistema en alcanzar por primera vez el 50% de su valor final.
-
Tiempo de crecimiento: Lo que tarda la respuesta en pasar del 0 al 100% de su valor en un estado estacionario
-
Tiempo de establecimiento: Lo que tarda la respuesta en alcanzar y mantenerse en un rango alrededor del valor final establecido en ±5%
-
Tiempo de pico: Tiempo requerido para que la respuesta alcance el primer pico del sobreimpulso.
-
Sobreimpulso máximo: El valor máximo de la respuesta medido desde la unidad.
![]()
Descripción del experimento
La planta montada en el laboratorio consta de diferentes partes, como son entre otras:
-
Ventilador
-
Plancha
-
Acondicionador
-
Actuador
Esta planta actuará como un sistema de segundo orden generando una respuesta que bien no es totalmente igual que la de una de segundo orden, si la podemos asemejar. Para comprobarlo necesitamos el actuador que se encarga de generar señales escalón, las cuales queremos estudiar para medir su respuesta. Este actuador, actúa sobre el pequeño motor que da el funcionamiento al ventilador, el cual se mueve haciendo que la plancha se mueva también. En el eje de sujeción hay un potenciómetro cuya señal varía según el movimiento de la pala y que va a un sensor.
Para introducir la señal de control en el sistema utilizaremos la tarjeta “SIGLAB”. Esta tarjeta consta de cuatro entradas y dos salidas. De uno de los canales de entrada está conectado el actuador, por donde se introduce la señal escalón se encuentra el ganador de pulso y el acondicionador.
Todo esto está controlado por entorno MATLAB donde podemos encontrar diferentes opciones, una de ellas es un osciloscopio cuyo funcionamiento es el mismo que uno convencional, además de un generador de funciones, para introducir la función que queremos, escalón, rampa...
Entonces le introducimos los correspondientes datos necesarios para la obtención de los resultados:
-
Rango: (Canal 1 y 2) 5V
-
Frecuencia: (Canal 1) 0,2 Hz. Cada 5 seg un impulso.
-
Tensión de pico: 2V (Tensión alterna). Se ajusta el offset a 2V
Habilitamos todo. Y comienza a funcionar. El ventilador se acciona, levanta la tablilla y obtenemos muestras obteniendo la siguiente respuesta:
Que como podemos comprobar se asemeja a la respuesta de un sistema de segundo orden.
Obtención de resultados
Una vez obtenido esta respuesta podemos calcular todos los parámetros que se piden:
Primero los calcularemos por resultado en el laboratorio.
Para sacar los resultados que buscamos el programa tiene la opción de poder hacer zoom todas las veces que queramos. Entonces observando obtenemos:
-
Utilizamos el zoom hasta observar donde se encuentra nuestro 0. En nuestro caso se encuentra en 0,3125 sec.
-
Con el ratón no situamos en la altura máxima del primer pico de la gráfica de la respuesta. Este es el tiempo de pico = 0,34765 sec. (Este valor es respecto a nuestro 0)
-
Seguimos observando la pantalla y podemos observar los siguientes resultados:
y(tp)=3,817 V
y(")=3,186 V
Con lo que ya podemos obtener el sobreimpulso máximo.
![]()
= 19,805%
A partir de aquí tendremos en cuenta las expresiones dadas en el enunciado, necesarias para la resolución del problema.
Sabiendo que:

![]()
![]()
Podemos observar que el factor de amortiguamiento es del tipo 0 < ![]()
< 1, es decir sistema subamortiguado, como era de esperar a la vista de la respuesta.
-
Podemos también observar en la pantalla el tiempo de establecimiento = 0,7578 sec.
Utilizando la expresión ![]()
podemos obtener la frecuencia natural.
![]()
Y también sabemos las siguientes expresiones.
-

y
donde:

![]()
Que sustituyendo los valores correspondientes obtenemos:

![]()
![]()
que es el tiempo de crecimiento.
Con todos estos valores estamos en condiciones de sacar la función de transferencia


Con esta función de transferencia ya puedo hallar la respuesta en frecuencia (Diagrama de Bode), que lo haremos de dos formas:
-
Con Simulink
-
Con espacio de trabajo Matlab.
SIMULINK
En el primer cuadro de diálogo pongo fdt, y continúo haciendo click en la siguiente serie:
Para inmediatamente seguir con la siguiente serie:
Los componentes que nos van haciendo falta los vamos arrastrando y colocándolos en pantalla.
Hago doble click en el analizador de espectro y de descripción y seguimos pasos de conexión. Inmediatamente después seguimos el siguiente proceso:
Con esto mejoro la salida de la onda en pantalla.
Ya la doy a Simular y obtengo los siguientes resultados.
ENTORNO MATLAB
Vamos a ir por pasos explicando cada cosa, dando las órdenes y viendo lo que sale en pantalla.
Definimos numerador y denominador
Nume=[81.93]
Deno=[1 8.146 81.93]
Función de transferencia
printsys (Nume,Deno,'s')
En pantalla
Asignamos variables ceros, polos y ganancia
[cero,polo,ganancia]=tl2zp (Nume,Deno)
Vamos a ver ahora el amortiguamiento y la frecuencia natural
[frec,amort]=damp(Deno)
Respuesta ante escalón unitario (Definimos vector de tiempo)
t=[0 : 0.01 : 3]
Definimos dos nuevas variables, x e y, que van a ser la función escalón
[y,x]=step [Nume,Deno,t]
Para dibujarlo
plot (t,y)
Ahora vamos a hallar la respuesta en frecuencia (Definimos el vector frecuencia)
w=[0.1 : 1 : 10000]; (El punto y coma para que no aparezca resultado en pantalla)
Diagrama de Bode
bode (Nume,Deno,w)
1
0 dB
wn
-40 dB/dec
Depende de ![]()
.Si este es pequeño la cresta es mayor y viceversa
wn
w
-90º
-180º
Barra de tareas -> Simulación -> Parámetros -> Define factor
Sources -> Sineware uno
Blocksets tool boxe -> Simulink extras -> Addiootional sinak -> Spectrum analyzer
MODULO
FASE
FRECUENCIA
![]()
0,5
1
1,2
Cero= Empty
Polo=
-4.0730+8.0384i
-4.0730-8.0834i
Ganancia=
81.93
frec= 9.0515
9.0515
amort= 0.45
0.45
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | España |
