Equipos e instalaciones electrotécnicas
Simplificación de funciones
Memória 2
Simplificación de funciones
1.- Ejercicio
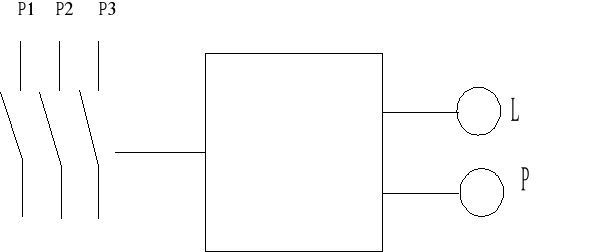
Una prensa se pone en marcha mediante la actuación simultanea de 3 pulsadores. Si se pulsan solamente dos cualquiera la prensa funcionará, pero se activara una lámpara indicando una manipulación incorrecta. Cuando se pulse un solo dispositivo también se encenderá pero no se activará la prensa.
|
P1 | P2 | P3 | L | P |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
FL =A · B· C + A · B · C + A · B · C + A · B · C + A · B · C + A · B · C
| a b c | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 |
B · C
A · B
A · C
FL= A · C + A · B + B · C
FP = A · B· C + A · B · C + A · B · C + A · B · C
Karnaugh de la prensa
| a b c | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 | 1 | |||
| 1 | 1 | 1 | 1 |
A · B
A · C
B · C
FP = A · B + A · C + B · C
A A B B C C
FP
FL
2.- Ejercicios de simplificación
A) F= A · B· C + A · B · C + A · B · C + A · B · C + A · B · C
| a b c | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 |
A
B · C
F= A + B · C
B) F= A · B· C + A · B · C + A · B · C + A · B · C + A · B · C + A · B · C + A · B · C
| a b c | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
A A
B C
F= A + B · C
C) F= A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D
| a c b d | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | 1 | 1 | ||
| 0 1 | 1 | 1 | ||
| 1 1 | 1 | |||
| 1 0 |
A · C
A · B · D
F= A · C + A · B · D
D) F= A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D +
A · B · C · D + A · B · C · D
| a c b d | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | 1 | 1 | ||
| 0 1 | 1 | 1 | ||
| 1 1 | 1 | 1 | ||
| 1 0 | 1 |
A · C
A · B
A · D
F= A · C + A · B + A · D
3.- Ejercicio de simplificación
| a | b | c | d | S | S2 | S3 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Simplifica la siguiente tabla de la verdad utilizando minterm
S
F= A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D +
A · B · C · D + A · B · C · D
| a c b d | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | ||||
| 0 1 | 1 | |||
| 1 1 | 1 | 1 | 1 | 1 |
| 1 0 | 1 | 1 |
F= A · B · C + C · D + B · C
S2
F= A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D +
A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D
| a c b d | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | 1 | 1 | 1 | 1 |
| 0 1 | 1 | 1 | ||
| 1 1 | 1 | 1 | 1 | 1 |
| 1 0 |
F= C · D + C · D + A · B · D + A · B · D
S3
F= A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D +
A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D
| a c b d | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | 1 | 1 | ||
| 0 1 | 1 | |||
| 1 1 | 1 | 1 | 1 | 1 |
| 1 0 | 1 | 1 | 1 | 1 |
F= A · D + A · B · D + C
Conclusion
La simplicación de funciones es muy importante ya que te permite ahorrar tiempo y cable. Al hacer la ximplificación es muy importante k los grupos de unos seleccionados sean del mayor numero posible (2, 4, 8...) para llegar a simplificar mas la función. Siempre en que en cada una de las puntas de la tabla de simplicacion los 1 se podran juntar, la parte de la derecha de la tabla se junta con la de la izquierda y la de arriba con la de abajo, para permitir hacer un menor numero de grupos.
4.- Ejercicio
Un sistema autamático de información posee 4 pulsadores, con 2 posiciones cada uno, que pueden indicar un si o un no. Asi mismo posee 3 lámparas, de las cuáles la primera se enciende cuando el resultado de la botación és afirmativo, la segunda cuando es negativo y l 3era cuando hay un empate. Diseñad un circuito con las especificaciones pedidas y el menor numeo de puertas posible.
| a | b | c | d | L1 | L2 | L3 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Si F= A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D
| a c b d | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | ||||
| 0 1 | 1 | |||
| 1 1 | 1 | 1 | 1 | |
| 1 0 | 1 |
F= A · B · D + A · C · D + A · B · C + B · C · D
No F= A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D
+ A · B · C · D
| a c b d | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | 1 | 1 | 1 | |
| 0 1 | 1 | |||
| 1 1 | ||||
| 1 0 | 1 |
F= A · C · D + B · C · D + A · B · D + A · B · C
= F = A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D
+ A · B · C · D
| a c b d | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | 1 | |||
| 0 1 | 1 | 1 | ||
| 1 1 | 1 | |||
| 1 0 | 1 | 1 |
Si
=
No
Descargar
| Enviado por: | Eduard Martínez |
| Idioma: | castellano |
| País: | España |
