Matemáticas
Serie de Fourier y transformada de Laplace
Universidad Interamericana del Norte
Materia: Matemáticas
Alumno: Miguel Ángel Martínez Durán
Tema: Serie de Fourier y Transformada de Laplace Serie de Fourier generalizada
Supongamos que ![]()
es un conjunto infinito ortogonal de funciones en un intervalo [a,b]. Nos preguntamos: si y=f(x) es una función definida en el intervalo [a,b], ¿será posible determinar un conjunto de coeficientes ![]()
0, 1, 2,..., para el cual
![]()
Como en la descripción anterior, cuando determinamos los componentes de un vector, también podemos determinar los coeficientes ![]()
mediante el producto interno. Al multiplicar la ecuación anterior por ![]()
e integrar en el intervalo [a,b] se obtiene
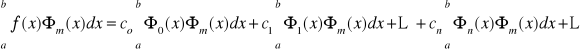
![]()
Debido a la ortogonalidad, cada término del lado derecho de la última ecuación es cero, excepto cuando m=n. En este caso tendremos
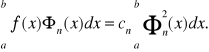
Entonces los coeficientes que buscamos son
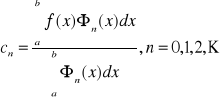
En otras palabras, ![]()
(1)
En la que 
(2)
La ecuación 2, en notación de producto interno ( o producto punto ), es

(3)
El conjunto de funciones

(1)
es ortogonal en el intervalo [-p,p], supongamos que f es una función definida en el intervalo [-p,p] que se puede desarrollar en la serie trigonométrica
![]()
(2)
Entonces, los coeficientes ![]()
pueden determinar tal como describimos para la serie de Fourier generalizada en la sección anterior.
Al integrar ambos lados de la ecuación (2), desde -p hasta p, se obtiene
![]()
(3)
Como cada función ![]()
, ![]()
n>1, es ortogonal a 1 en el intervalo, el lado derecho de (3) se reduce a un solo término y, en consecuencia,
![]()
Al despejar ![]()
se obtiene
![]()
(4)
Ahora multipliquemos la ecuación (2) por ![]()
e integremos:
![]()
(5)
por la ortogonalidad tenemos que
![]()
![]()
y
Entonces la ecuación 5 se reduce a ![]()
Y así ![]()
(6)
Por último si multiplicamos a (2) por ![]()
, integramos y aplicamos los resultados
![]()
![]()
![]()
llegamos a ![]()
(7)
La serie de Fourier de una función definida en el intervalo (-p,p) es
![]()
(8)
![]()
(9)
![]()
(10)
![]()
(11)
Series de Fourier de cosenos y de senos
Si f es una función par en (-p,p), entonces en vista de las propiedades anteriores, los coeficientes de (9),(10) y (11) se transforman en
![]()
![]()
![]()
.
En forma parecida, cuando f es impar en el intervalo (-p,p),
![]()
, n=0,1,2,..., ![]()
Resumiendo quedaría de la siguiente manera:
La serie de Fourier de una función par en el intervalo (-p,p) es la serie de cosenos
![]()
en que ![]()
![]()
b) La serie de Fourier de una función impar en el intervalo (-p,p) es la serie . de senos
![]()
en donde ![]()
Transformada de Laplace
Definición básica. Si f(t) está definida cuando ![]()
, la integral impropia ![]()
se define como un límite:
![]()
Si existe un límite se dice que la integral existe o que es convergente, si no existe el límite, la integral no existe y se dice que es divergente. En general el límite anterior existe sólo para ciertos valores de la variable s. La situación ![]()
proporciona una transformación lineal muy importante:
Sea f una función definida para ![]()
. Entonces la integral
![]()
se llama transformada de Laplace de f, siempre y cuando la integral converja.
Evaluar L{1}.
Solución ![]()
![]()
L ![]()
es una transformada lineal, para una suma de funciones se puede escribir
![]()
siempre que las dos integrales converjan; por consiguiente,
![]()
Se dice que L es una transformada lineal debido a la propiedad señalada en la función anterior
Condiciones suficientes para la existencia
Si f (t) es continua por tramos en el intervalo ![]()
y de orden exponencial c para t>T, entonces L {f(t)} existe para s>c.
Demostración ![]()
La integral ![]()
existe, porque se puede expresar como una suma de integrales sobre intervalos en que ![]()
es continua. Ahora
![]()
![]()
cuando s>c. Como ![]()
converge, la integral ![]()
converge, de acuerdo con la prueba de comparación para integrales impropias. Esto a su vez, implica que ![]()
existe para s>c. La existencia de ![]()
e ![]()
implica que ![]()
existe cuando s>c.
Transformadas de algunas funciones básicas
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) f) ![]()
g) ![]()
Transformada inversa
Se dice que f(t) es la transformada inversa de Laplace de F(s) y se expresa:
![]()
Algunas transformadas inversas
a) b)
c) d)
e) f)
g)
es una transformada lineal. Suponemos que la transformada inversa de Laplace es, en sí, una transformación lineal; esto es, si ![]()
y ![]()
son constantes,
![]()
en donde F y G son las transformadas de las funciones f y g.
La transformada inversa de Laplace de una función F(s) puede no ser única. Es posible que ![]()
y, sin embargo, ![]()
.
Comportamiento de F(s) cuando ![]()
Si f(t) es continua por tramos en ![]()
y de orden exponencial para t>T, entonces ![]()
Demostración Dado que f(t) es continua parte por parte en ![]()
, necesariamente es acotada en el intervalo; o sea ![]()
. También ![]()
cuando t>T. Si M representa el máximo de ![]()
y c indica el máximo de ![]()
, entonces

para s>c. Cuando ![]()
, se tiene que ![]()
, de modo que ![]()
.
Teoremas de traslación
Primer teorema de traslación
Si F(s)=L{f(t)} y a es cualquier número real,
![]()
Demostración La demostración es inmediata
![]()
Segundo teorema de traslación
Si ![]()
y a>0, entonces
![]()
Demostración Expresamos a ![]()
como la suma de dos integrales:

![]()
.
Ahora igualamos v=t-a,dv=dt y entonces
![]()
![]()
Derivadas de transformadas
Si ![]()
y n=1,2,3,..., entonces

Transformada de una derivada
Si f(t), f'(t),..., ![]()
son continuas en ![]()
, son de orden exponencial, y si ![]()
es continua parte por parte ![]()
, entonces
![]()
en donde ![]()
Teorema de la convolución
Si f(t) y g(t)son continuas por tramos en ![]()
y de orden exponencial,
![]()
Demostración Sean
Y .
Al proceder formalmente obtenemos
![]()
![]()
![]()
Mantenemos fija ![]()
y escribimos ![]()
, de modo que
![]()
Transformada de una función periódica
Si f(t) es continua por tramos en ![]()
, de orden exponencial y periódica con periodo T,

(a)
Demostración Expresamos la transformada de Laplace como dos integrales:
![]()
(b)
Escribiendo t=u+T, la última de las integrales de (a) se transforma en
![]()
Por consiguiente, la ecuación (b) es ![]()
Al despejar ![]()
se llega al resultado de la ecuación (a).
Descargar
| Enviado por: | Miguel Ángel Martínez Durán |
| Idioma: | castellano |
| País: | México |
