Matemáticas
Sección áurea
SECCION AÚREA
Introducción
Hagamos un experimento: dibujemos una recta de la dimensión que deseemos. Fijémonos bien en ella , después, dividámosla en dos partes desiguales mediante un pequeño trazo, de tal manera que los dos segmentos sean equilibrados y proporcionalmente agradables. Tras esto midámoslas, podremos comprobar que la menor es aproximadamente un 62% de la mayor y que ésta es un 62% de la recta completa. Fray Paciolo di Borgo, monje italiano, enuncio en el 1509 una fórmula matemática cuya aplicación da una constante a la que denominó Número de Oro o Divina Proporción. Ya utilizada en la antigüedad ésta Divina Relación se encuentra cuando, realizando el ejercicio anterior, el segmento menor, es al segmento mayor, como este es a la suma de ambos, es decir, a la totalidad de la recta. Este número equivale al 62% y es exactamente 0.618.
Trabajo de la sección Áurea
A lo largo del tiempo todos los artistas han buscado una forma de división de las cosas perfectas pero no había nada que indicase en que proporción debían estar las cosas(seres vivos, objetos...).Ahora sabemos que existe una fórmula muy conocida en el mundo del diseño, que permite dividir el espacio en partes iguales, para lograr un efecto estético agradable y que puede llegar a ser muy eficaz. Esta teoría se denomina "La regla Áurea", también conocida como "divina proporción" o “numero áureo”
En 1497, un fraile italiano llamado Lucca Pacioli escribió un libro donde se reveló, por fin, el secreto de la belleza. Se titula De divina Proportione, y su tema central es lo que los escolares de nuestros días conocen como "regla de tres". Pacioli se inspiraba en las ideas de Piero della Francesca, un hombre que hoy conocemos a través de su obra pictórica, pero que en su tiempo era más conocido por ser el autor de De Abaco, un manual de matemática para comerciantes.
La regla de tres era una herramienta básica para los comerciantes del Quattrocento: servía para determinar las proporciones de capital, tierras, volumen de grano o cualquier otra clase de bienes que le correspondía a cada socio, heredero o copropietario ante un total determinado. Se la conocía entonces como regla de oro o llave del comerciante.
Una regla de tres famosa es la llamada Escala Armónica Pitagórica, que al modo renacentista se expresa: 6 8 9 12
Algunos arquitectos relacionaron la escala armónica pitagórica, utilizada para representar una escala musical, con el diseño visual modular o proporcional. Andrea Palladio dejó asentada una falacia de diseño según la cual los espacios pueden ser diseñados "musicalmente" de acuerdo con esta escala: como el intervalo entre 6 y 12 es de una octava, entre 6 y 9 y entre 8 y 12 es de una quinta, entre 6 y 8 y entre 9 y 12 de cuarta y entre 8 y 9 de un tono, si se organizaban las dimensiones de las habitaciones de un edificio siguiendo esta serie, entonces se estaría produciendo una armonía espacial de la misma clase que la que relaciona las notas musicales. La regla Áurea parecía una fórmula perfecta que relacionaba las artes de la música, la pintura y la arquitectura. Y además mantenía las buenas relaciones comerciales.
Cuando Lucca Pacioli escribió La Divina Proporción, lo que hizo fue tomar otro tipo de regla de tres, que, partiendo de una unidad arbitraria permitía la construcción de proporcionalidades tanto de múltiplos como de submúltiplos (intervalos mayores y menores). Los aficionados (en particular los fotógrafos, grandes entusiastas) conocen esta relación como sección áurea. Su expresión matemática es
a:b=b:a+b
Vitruvio ideó un sistema de cálculo matemático de la división pictórica, para seccionar los espacios en partes iguales y así conseguir una mejor composición. Se basa en el principio general de contemplar un espacio rectangular dividido, a grandes rasgos, en terceras partes, tanto vertical como horizontalmente. O, explicado de otra forma, bisecando un cuadro y usando la diagonal de una de sus mitades como radio para ampliar las dimensiones del cuadrado hasta convertirlo en "rectángulo áureo". Se llega a la proporción a:b = c:a. Al situar los elementos primordiales de diseño en una de estas líneas, se cobra conciencia del equilibrio creado entre estos elementos y el resto del diseño.
Rectángulo áureo
| Un rectángulo especial es el llamado rectángulo áureo. Se trata de un rectángulo armonioso en sus dimensiones. | ||
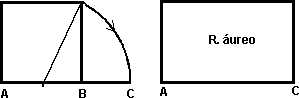
| Dibujamos un cuadrado y marcamos el punto medio de uno de sus lados. Lo unimos con uno de los vértices del lado opuesto y llevamos esa distancia sobre el lado inicial, de esta manera obtenemos el lado mayor del rectángulo. |
| |
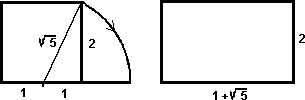
| Si el lado del cuadrado vale 2 unidades, es claro que el lado mayor del rectángulo vale 1+ 5 por lo que la proporción entre los dos lados es: (1+ 5 ) /2 |
| |
A este número se le llama número de oro, se representa por el símbolo Ø y su valor es 1,61803..., lo obtuvieron los griegos al hallar la relación entre la diagonal de un pentágono y el lado. El nombre de "número de oro" se debe a Leonardo da Vinci.
|
| En "el hombre ideal" de Leonardo, el cociente entre el lado del cuadrado y el radio de la circunferencia que tiene por centro el ombligo, es el número de oro. |
|
| Otra propiedad de este rectángulo es que si se colocan dos iguales como en la figura de la derecha, se forma otro rectángulo áureo más grande. |
|
.
Los egipcios ya conocían esta proporción y la usaron en la arquitectura de la pirámide de Keops (2600 años a.C.). Los Egipcios descubrieron la proporción áurea por análisis y observación, buscando medidas que les permitiera dividir la tierra de manera exacta., a partir del hombre, utilizando la mano, el brazo, hasta encontrar que media lo mismo de alto que de ancho con los brazos extendidos y encontraron que el ombligo establecía el punto de división en su altura y esta misma ,se lograba de manera exacta, rebatiendo sobre las bases de un cuadrado, una diagonal trazada de la mitad de la base a una de sus aristas. La proporción áurea, paso de Egipto a Grecia y de allí a Roma. Las más bellas esculturas y construcciones arquitectónicas están basadas en dichos cánones.
| Aparece en pinturas de Dalí, en la Venus de Boticelli. Esta razón también la usaron en sus producciones artistas del Renacimiento. En España, en la Alambra, en edificios renacentistas como El Escorial ... y en la propia Naturaleza en las espirales de las conchas de ciertos moluscos. |
|
|
| Los griegos también la usaron en sus construcciones, especialmente El Partenón, cuyas proporciones están relacionadas entre sí por medio de la razón áurea. |
El símbolo Ø para la relación áurea fue elegido por el matemático americano Mark Barr. La letra fue elegida porque era la primera del nombre de Phidias que solía usar la relación áurea en sus esculturas.
También se ha usado en el diseño del DNI, en la construcción de muebles, marcos para ventanas, camas, etc.
La sucesión de Fibonacci
Consideremos la siguiente sucesión de números:
1, 1, 2, 3, 5, 8, 13, 21, 34...
Cada número a partir del tercero, se obtiene sumando los dos que le preceden. Por ejemplo, 21 = 13 + 8; el siguiente a 34 será 34 + 21 = 55.
Esta sucesión es la llamada "sucesión de Fibonacci" (Leonardo de Pisa 1170-1240).
Los cocientes (razones) entre dos números de la sucesión, se aproximan más y más al número áureo (1'61803...).
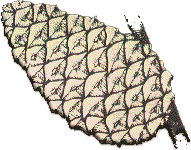
| Esta sucesión de números aparece en la Naturaleza en formas curiosas. Las escamas de una piña aparecen en espiral alrededor del vértice. Si contamos el número de espirales de una piña, encontraremos que siempre es igual a uno de los números de la sucesión de Fibonacci. |
|
|
| Esta sucesión también aparece en el estudio de las leyes mendelianas de la herencia, en la divergencia foliar, en la formación de la concha de algunos moluscos... |
|
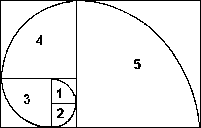
| Una manera práctica de dibujar una espiral es mediante la construcción rectangular en las espirales de cuadrados; se trata de dibujar el cuadrante de un círculo en cada nuevo cuadrado que se añada. |
En la construcción anterior, se empieza con un cuadrado de 1 unidad de lado (el nº 1), se añade uno igual para formar un rectángulo de 2 x 1, a continuación añadimos un cuadrado de 2 x 2 (el nº 3) para formar un rectángulo de 3 x 2; después un cuadrado de 3 x 3 (el nº 4), de manera que el siguiente rectángulo es 5 x 3, el siguiente cuadrado es 5 x 5 (el nº 5), y así sucesivamente.
Sucesión de Fibonacci y la regla Áurea
Consideremos la siguiente sucesión de números: 1, 1, 2, 3, 5, 8, 13, 21...
| Las razones entre ellos son: |
|
Si cogemos dos números cualesquiera como números de partida y formamos una sucesión de Fibonacci sumando siempre los dos últimos números, las razones serian:
Empezamos por 3 y 7; la sucesión sería: 3, 7, 10, 17, 27, 44, 71, 115...
| Las razones son: |
|
Independientemente de los números que encabecen la sucesión, las razones se aproximan más y más al número 1'61803...
Este número fue estudiado por los griegos. Estamos ante el numero áureo, su valor
| exacto es: |
| y se representa con el símbolo Ø. |
| Los griegos obtuvieron este número al hallar la relación entre la diagonal del pentágono regular y su lado. Esto hace posible construir un pentágono regular usando regla y compás.
|
|
|
| Al trazar las diagonales de un pentágono resulta la estrella pentagonal o estrella de Italia, era el símbolo de la escuela pitagórica y servía a los pitagóricos para reconocerse entre sí. |
Índice
Portada ............................................................................................................................... pagina 1
Índice ............................................................................................................................... pagina 2
Introducción ....................................................................................................................... pagina 3
Trabajo ............................................................................................................................... pagina 3-10
Bibliografía ........................................................................................................................ pagina 11
Bibliografía
E recopilado la información de este trabajo buscando en la Enciclopedia Encarta 2000 y buscando en www.google.com donde encontré información en bastantes paginas web, algunas de estas web son las siguientes:
http://www.newsartesvisuales.com/funda/compo4.htm
http://www.geocities.com/ResearchTriangle/Thinktank/4492/noticias/la_proporcion_aurea.htm
http://www.cnice.mecd.es/recursos/bachillerato/arte/arte/pintura/fibonaci.htm
Descargar
| Enviado por: | Alfredo_getafe_i.e.s_puig Adam |
| Idioma: | catalán |
| País: | España |