Estadística
Regresión Lineal Simple
Regresión Lineal Simple
Generalidades
La regresión y los análisis de correlación nos muestran como determinar tanto la naturaleza como la fuerza de una relación entre dos variables
En el análisis de regresión desarrollaremos una ecuación de estimación, esto es, una formula matemática que relaciona las variables conocidas con la variable desconocida. Entonces podemos aplicar el análisis de correlación para determinar el grado de en el que están relacionadas las variables. El análisis de correlación, entonces, nos dice qué tan bien están relacionadas las variables. El análisis de correlación, entonces, nos dice que tan bien la ecuación de estimación realmente describe la relación
Principales técnicas utilizadas en el análisis de regresión lineal simple
1) Ordenamiento y análisis de la información original
3) Diagrama de dispersión e interpretación
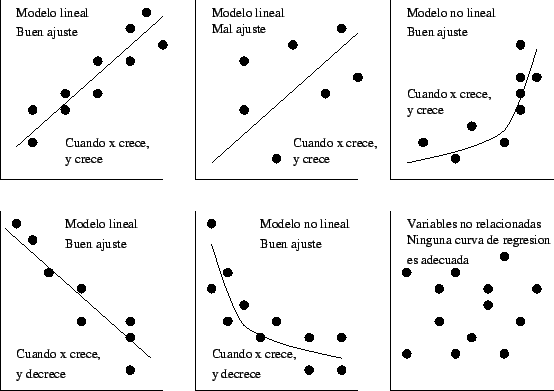
El primer paso para determinar si existe o no una relación entre dos variables es observar la grafica de datos observados. Esta grafica se llama diagrama de dispersión.
Un diagrama nos puede da dos tipos de información, visualmente podemos buscar patrones que nos indiquen que las variables están relacionadas. Entonces si esto sucede, podemos ver que tipo de línea, o ecuación de estimación, describe esta relación.
Primero tomamos los datos de la tabla que deseamos analizar y dependiendo de que se desea averiguar se construye la grafica colocando la variable dependiente en el eje Y y la independiente en el eje X, Cuando vemos todos estos puntos juntos, podemos visualizar la relación que existe entre estas dos variables. Como resultado, también podemos trazar, “o ajustar” una línea recta a través de nuestro diagrama de dispersión para representar la relación. Es común intentar trazar estas líneas de forma tal que un numero igual de puntos caiga a cada lado de la línea.
Diagrama de dispersión
Estimación mediante la línea de regresión
Hasta el momento las líneas de regresión se colocaron al ajustar las líneas visualmente entre los puntos de datos, pero para graficar estas líneas de una forma más precisa podemos utilizar una ecuación que relaciona las dos variables matemáticamente.
La ecuación para una línea recta donde la variable dependiente Y esta determinada por la varianza dependiente X es:
Usando esta ecuación podemos tomar un valor dado en X y calcular el valor de Y la a se denomina intersección en Y por que su valor es el punto en el cual la línea de regresión cruza el eje Y por que su valor es el punto en el cual la línea de regresión cruza el eje Y, es decir el eje vertical. La b es la pendiente de la línea, representa que tanto cada cambio de unidad de la variable independiente X cambia la variable dependiente Y. Tanto a como b son constantes numéricas, puesto que para cada recta dada, sus valores no cambian.
Recta de regresión por el método de mínimos cuadrados.
Ahora que hemos visto como determinar la ecuación para una línea recta, pensemos como podemos calcular una ecuación para una línea dibujada en medio de un conjunto de puntos en un diagrama de dispersión. Para esto debemos minimizar el error entre los puntos estimados en la línea y los verdaderos puntos observados que se utilizaron para trazarla.
Para esto debemos introducir un nuevo símbolo, para simbolizar los valores individuales de los puntos estimados, esto es, aquellos puntos que caen en la línea de estimación. En consecuencia escribiremos la ecuación para la línea de estimación como
Una forma en que podemos medir el error de nuestra línea de estimación es sumando todas las diferencias, o errores, individuales entre los puntos observados y los puntos estimados.
La suma de las diferencias individuales para calcular el error no es una forma confiable de juzgar la bondad de ajuste de una línea de estimación.
El problema al añadir los errores individuales es el efecto de cancelación de los valores positivos y negativos, por eso usamos valores absolutos en esta diferencia a modo de cancelar la anulación de los signos positivos y negativos, pero ya que estamos buscando el menor error debemos buscar un método que nos muestre la magnitud del error, decimos que la suma de los valores absolutos no pone énfasis en la magnitud del error.
Parece razonable que mientras más lejos este un punto de la línea e estimación, mas serio seria el error, preferiríamos tener varios errores pequeños que uno grande. En efecto, deseamos encontrar una forma de “penalizar” errores absolutos grandes, de tal forma que podamos evitarlos. Puede lograr esto si cuadramos los errores individuales antes de sumarlos. Con estos se logran dos objetivos:
penaliza los errores más grandes
cancela el efecto de valores positivos y negativos
Como estamos buscando la línea de estimación que minimiza la suma de los cuadrados de los errores a esto llamamos método de mínimos cuadrados.
Si usamos el método de mínimos cuadrados, podemos determinar si una línea de estimación tiene un mejor ajuste que otro. Pero para un conjunto de puntos de datos a través de los cuales podríamos trazar un numero infinito de líneas de estimación, ¿cómo podemos saber cuando hemos encontrado la mejor línea de ajuste?
Los estadísticos han derivado dos ecuaciones que podemos utilizar para encontrar la pendiente y la intersección Y de la línea de regresión del mejor ajuste. La primera formula calcula la pendiente.
-
b = pendiente de la línea de estimación de mejor ajuste
-
X = valores de la variable independiente
-
Y = valores de la variable dependiente
-
= media de los valores de la variable independiente
-
= media de los valores de la variable dependiente
-
n = numero de puntos de datos
La segunda ecuación calcula la intersección en Y
-
a = intersección en Y
-
b = pendiente de la ecuación anterior
-
= media de los valores de la variable dependiente
-
= media de los valores de la variable independiente
Verificación de la ecuación de estimación
Ahora que sabemos como calcular la línea de regresión, podemos verificar que tanto se ajusta.
Tomando los errores individuales positivos y negativos deben dar cero
5) Error estándar de la estimación
El error estándar nos permite deducir la confiabilidad de la ecuación de regresión que hemos desarrollado.
Este error se simboliza Se y es similar a la desviación estándar en cuanto a que ambas son medidas de dispersión.
El error estándar de la estimación mide la variabilidad, o dispersión de los valores observados alrededor de la línea de regresión y su formula es la siguiente
-
= media de los valores de la variable dependiente
-
Y = valores de la variable dependiente
-
n = numero de puntos de datos
Método de atajo para calcular el error estándar de la estimación
Dado que utilizar la ecuación anterior requiere una serie de cálculos tediosos, se ha diseñado una ecuación que puede eliminar unos de estos pasos, la ecuación es la siguiente:
-
X = valores de la variable independiente
-
Y = valores de la variable dependiente
-
a = intersección en Y
-
b = pendiente de la ecuación de la estimación
-
n = numero de puntos de datos
interpretación del error estándar de la estimación
Como se aplicaba en la desviación estándar, mientras más grande sea el error estándar de estimación, mayor será la dispersión de los puntos alrededor de la línea de regresión. De manera que inversa, si Se = 0, esperemos que la ecuación de estimación sea un estimador perfecto de la variable dependiente. En este caso todos lo puntos deben caer en la línea de regresión y no habría puntos dispersos.
Usaremos el error estándar como una herramienta de igual forma que la desviación estándar. Esto suponiendo que los puntos observados están distribuidos normalmente alrededor de la línea de regresión, podemos encontrar un 68% de los puntos en + 1 Se, 95.5% en + 2 Se y 99.7% de los puntos en + 3 Se. Otra cosa que debemos observar es que el error estándar de la estimación se mide a lo largo del eje Y, y no perpendicularmente de la línea de regresión.
Intervalos de confianza utilizando desviación estándar
En estadística, la probabilidad que asociamos con una estimación de intervalo se conoce como el nivel de confianza
Esta probabilidad nos indica que tanta confianza tenemos en que la estimación del intervalo incluya al parámetro de la población. Una probabilidad mas alta significa mas confianza.
El intervalo de confianza es el alcance de la estimación que estamos haciendo pero a menudo hacemos el intervalo de confianza en términos de errores estándar, para esto debemos calcular el error estándar de la media así:
Donde es el error estándar de la media para una población infinita, es la desviación estándar de la población.
Con frecuencia expresaremos los intervalos de confianza de esta forma: en la que:
= limite superior del intervalo de confianza
= limite inferior del intervalo de confianza
Relación entre nivel de confianza e intervalo de confianza
Podría pensarse que deberíamos utilizar un alto nivel de confianza, como 99% en todos los problemas sobre estimaciones, pero en algunos casos altos niveles de confianza producen intervalos de confianza alto por lo tanto imprecisos.
Debe tenerse un intervalo de confianza que vaya de acuerdo al tema que se este estimando.
6) intervalos de predicción aproximados
una forma de ver el error estándar de la estimación es concebirla como la herramienta estadística que podemos usar para hacer un enunciado de probabilidad sobre el intervalo alrededor del valor estimado de , dentro del cual cae el valor real de Y.
Cuando la muestra es mayor de 30 datos, se calcula los intervalos de predicción aproximados de la siguiente manera,
Si queremos estar seguros en aproximadamente 65% de que el valor real de Y caerá dentro de + 1 error estándar de . Podemos calcular los limites superior e inferior de este intervalo de predicción de la siguiente manera:
= Limite superior del intervalo de predicción
= Limite inferior del intervalo de predicción
Si, en lugar decimos que estamos seguros en aproximadamente 95.5% de que el dato real estará dentro de + 2 errores estándar de la estimación de . Podríamos calcular los limites de este intervalo de la siguiente manera:
= Limite superior del intervalo de predicción
= Limite inferior del intervalo de predicción
y por ultimo decimos que estamos seguros en aproximadamente el 99.7% cuando usamos + 3 errores estándar de la estimación de Podríamos calcular los limites de este intervalo de la siguiente manera:
= Limite superior del intervalo de predicción
= Limite inferior del intervalo de predicción
Como ya habíamos mencionado solo se usa para grandes muestras (mayores de 30 datos) para muestras más pequeñas se usan la distribución T
Debemos poner énfasis en que los intervalos de predicción son solo aproximaciones, de hecho los estadísticos pueden calcular el error estándar exacto para la predicción Sp, usando la formula:
en la que:
X0 = valor especifico de x en el que deseamos predecir el valor de Y
Análisis de correlación
El análisis de correlación es la herramienta estadística que podemos usar para describir el grado hasta el cual una variable esta linealmente relacionada con la otra. Con frecuencia el análisis de correlación se utiliza junto con el análisis de regresión para medir que tan bien la línea de regresión explica los cambio de la variable dependiente Y. Sin embargo, la correlación también se puede usar sola para medir el grado de asociación entre dos variables.
Los estadísticos han desarrollado dos medidas para describir la correlación entre dos variables: el coeficiente de determinación y el coeficiente de correlación.
Coeficiente de determinación
El coeficiente de determinación es la principal forma en que podemos medir la extensión, o fuerza de asociación que existe entre dos variables, X y Y. Puesto que hemos desarrollado una muestra de puntos para desarrollar las líneas de regresión, nos referimos a esta medida como el coeficiente de determinación de la muestra.
El coeficiente de determinación de la muestra se desarrolla de la relación entre dos tipos de variación: la variación de los valores Y en conjunto de los datos alrededor de
la línea de regresión ajustada
su propia media
el termino variación en estos dos casos se refiere a “la suma de un grupo de desviaciones cuadradas”. Al usar esta definición, entonces es razonable expresar la variación de los valores Y alrededor de la línea de regresión con esta ecuación:
variación de los valores Y alrededor de la línea de regresión =
la segunda variación, la de los valores de Y con respecto a su propia media, esta determinada por
variación de los valores de Y alrededor de su propia media =
uno menos la razón entre estas dos variaciones es el coeficiente de determinación de la muestra que se simboliza r2
esta ecuación es una medida del grado de asociación lineal entre X y Y
Una correlación perfecta es aquella en que todos los valores de Y caen en la línea de estimación , por lo tanto el coeficiente de determinación es 1
Cuando el valor del coeficiente de determinación es 0 quiere decir que no hay correlación entre las dos variables
En los problemas con que se topa la mayoría de los responsables de la toma de decisiones, r2 caerá en alguna parte entre estos dos extremos de 1 y 0. recuerde, no obstante que un r2 cercano a 1 indica una fuerte correlación entre X y Y, mientras que un r2 cercano a 0 significa que existe poca correlación entre estas dos variables.
Un punto que debemos subrayar fuertemente es que r2 mide solo la fuerza de una relación lineal entre dos variables.
Otra interpretación de r2
Los estadísticos también interpretan el coeficiente de determinación viendo la cantidad de variación en Y que es explicada por la línea de regresión.
Método de atajo para calcular el coeficiente de determinación (r2)
Hay una formula que nos ahorra muchos cálculos tediosos y esta es:
en la que:
-
r2= coeficiente de determinación de la muestra
-
a = intersección en Y
-
b = pendiente de la línea de estimación de mejor ajuste
-
n = numero de puntos de datos
-
X = valores de la variable independiente
-
Y = valores de la variable dependiente
-
= media de los valores observados de la variable dependiente
el coeficiente de correlación
el coeficiente de correlación es la segunda medida que podemos usar para describir que también una variable es explicada por la otra. Cuando tratamos con muestras, el coeficiente de variación de muestra se denomina como r y es la raíz cuadrada del coeficiente de determinación de muestra:
cuando la pendiente de estimación de la muestra es positiva, r es la raíz cuadrada positiva, pero si b es negativa, r es la raiz cuadrada negativa. Por lo tanto, el signo de indica la dirección de la relación entre las dos variables X y Y. Si existe una relación inversa, esto es , si y disminuye
Y
X
Intersección Y
Variable dependiente
Pendiente de la línea
Variable independiente
![]()
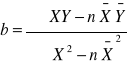
Descargar
| Enviado por: | Juan Carlos Riaño G |
| Idioma: | castellano |
| País: | España |
