Física
Refracción de la luz
Especialidad
Mecánica Industrial
Materia
Física III
-
Refracción de la Luz
Refracción de la luz es el cambio de dirección que experimenta un rayo al pasar de un medio menos refringente a otro más refringente.
Una cuchara introducida parcialmente en el agua, se ve quebrada en la parte donde hace contacto con la superficie del líquido.
La refracción de la luz consiste en la desviación de los rayos luminosos cuando ellos pasan de un medio a otro de distinta densidad óptica.
Para un observador situado en un medio menos denso, como el aire, un objeto situado en un medio más denso parece estar más cerca de la superficie de separación de lo que está en realidad. Un ejemplo habitual es el de un objeto sumergido, observado desde encima del agua, como se muestra en la figura 3 (sólo se representan rayos oblicuos para ilustrar el fenómeno con más claridad). El rayo DB procedente del punto D del objeto se desvía alejándose de la normal, hacia el punto A. Por ello, el objeto parece situado en C, donde la línea ABC intersecta una línea perpendicular a la superficie del agua y que pasa por D.
Leyes de la Refracción
Rayo Incidente, es aquel que llega a la superficie de separación de dos medios.
Rayo Refractado, el rayo que pasa al otro medio.
Ángulo de Incidencia, el ángulo que se forma entre el incidente y la normal.
Ángulo de Refracción, el ángulo formado por la normal y el rayo refractado.
Normal, es la perpendicular a la superficie de separación de los medios trazados.
Primera Ley de la Refracción
El rayo incidente, la normal y el rayo refractado pertenecen al mismo plano.
Segunda Ley de la Refracción o Ley de Snell
La razón o cociente entre el seno del ángulo de incidencia y el seno del ángulo de refracción es una constante, llamada índice de refracción, del segundo medio respecto del primero o sea:
| Sen i | = n | XXXXX | Del agua respecto al aire es n = 1.333 |
| Sen r | Del vidrio respecto del aire es n = 1.5 |
Relación entre la velocidad de la luz en el vacío y en medios transparentes
La relación entre la velocidad de la luz en el vacío o aire y la velocidad de la luz en otro medio material transparente se llama índice de refracción de la luz.
La velocidad de propagación de la luz en un medio material homogéneo y transparente es constante pero menor que la velocidad de propagación de la luz en el vacío.
Llamamos v1 y v2, a cada una de las velocidades respectivas y n al índice de refracción, tenemos:
| n = | v1 | XXXXX | n = índice de refracción |
| v2 | v1 = velocidad de la luz en el aire | ||
| v2 = velocidad de la luz en el otro medio |
Índices de refracción absolutos para la luz
Vacío 1.00
Aire 1.0000294
Agua 1.33
Alcohol etílico 1.36
Benceno 1.50
Vidrio 1.52
Diamante 2.42
Sal gema 1.54
Ácido sulfúrico 1.63
Éter 1.36
Hielo 1.32
Conocidos los índices de refracción podemos hallar la velocidad de la luz en estos medios.
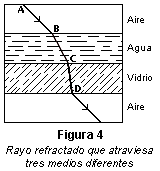
En la figura 4 se muestra la trayectoria de un rayo de luz que atraviesa varios medios con superficies de separación paralelas. El índice de refracción del agua es más bajo que el del vidrio. Como el índice de refracción del primer y el último medio es el mismo, el rayo emerge en dirección paralela al rayo incidente AB, pero resulta desplazado.
Problema
Hallar la velocidad de la luz en el Benceno, sabiendo que su índice de refracción es de 1.50 (la velocidad de la luz en el aire 300,000 km/s).
| Datos | x | Fórmula | x | Despeje | x | Sustitución | x | Resultado |
| v1 = 300,000 km/s | n = | v1 | v2 = | v1 | v2 = | 300,000 km/s | v2 = | 200,000 km/s |
| n = 1.50 | v2 | n | 1.5 |
| v2 = ? |
Problema
Hallar la velocidad de la luz en el vidrio, sabiendo que su índice de refracción es de 1.52.
| Datos | x | Fórmula | x | Despeje | x | Sustitución | X | Resultado |
| n = 1.52 | n = | v1 | v2 = | v1 | v2 = | 300,000 km/s | v2 = | 197,368 km/s |
| v1 = 300,000 km/s | v2 | n | 1.52 |
| v2 = ? |
El fulgor de las piedras preciosas, y sobre todo, del diamante es debido también a la reflexión total, pues este fenómeno es muy intenso en ellas por poseer un índice de refracción muy elevado y de ahí los variados destellos y tonalidades que presentan.
Refracción Atmosférica
La densidad de la atmósfera disminuye a medida que nos alejamos de la Tierra. Por eso los rayos luminosos en su trayectoria atraviesan capas de distinta densidad sin solución de continuidad. En dichas circunstancias el rayo se acerca a la normal.
La trayectoria de los rayos configuran una curva, pues la variación de densidad de la atmósfera es gradualmente progresiva debido a que las capas no se presentan perfectamente delimitadas. El astro solamente se observará sin variaciones de altura cuando esta en el cenit.
Por ello es que podemos ver el disco solar al amanecer y al atardecer cuando sólo su borde superior es tangente al horizonte.
Si no existiera refracción atmosférica el cielo ofrecería aspectos distintos.
Ángulo Límite
Ángulo límite es el ángulo de incidencia al que corresponde uno de refracción de 90°, cuando el rayo va de un medio más refringente hacia otro menos refringente.
Sea un foco de luz, de él parten infinidad de rayos, y al salir del medio más refringente al menos refringente, los rayos se separan de la normal y, por consiguiente, el ángulo de refracción es mayor que el de incidencia, si éste se va haciendo cada vez mayor y llegará un momento en que el rayo salga por la misma superficie de separación de los dos medios, y entonces el ángulo de refracción valdrá 90°. El ángulo de incidencia correspondiente se llama ángulo límite. El ángulo límite del agua es 48°; el de vidrio, 42°; el del diamante, 24°, etc.; que corresponden a los índices 1.3 y 2.4 respectivamente.
Reflexión Total
En el ángulo límite, el rayo sale por la misma superficie de separación, otro rayo incidente, que forme con la normal un ángulo mayor que el del límite, ya no saldrá al otro medio, sino que quedará dentro del mismo medio. Los ángulos que forman son iguales, como en la reflexión, este fenómeno se llama reflexión total. “Por reflejarse todos los rayos”.
Condiciones. La reflexión total se verifica:
Cuando el rayo va de un medio más refringente hacia otro menos refringente.
Cuando el ángulo de incidencia sea mayor que el del límite.
Ángulo crítico
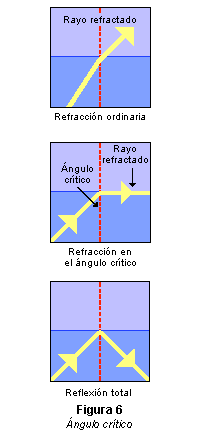
Puesto que los rayos se alejan de la normal cuando entran en un medio menos denso, y la desviación de la normal aumenta a medida que aumenta el ángulo de incidencia, hay un determinado ángulo de incidencia, denominado ángulo crítico, para el que el rayo refractado forma un ángulo de 90º con la normal, por lo que avanza justo a lo largo de la superficie de separación entre ambos medios. Si el ángulo de incidencia se hace mayor que el ángulo crítico, los rayos de luz serán totalmente reflejados. La reflexión total no puede producirse cuando la luz pasa de un medio menos denso a otro más denso. Las tres ilustraciones de la figura 6 muestran la refracción ordinaria, la refracción en el ángulo crítico y la reflexión total.
Espejismo
Es un fenómeno óptico que consiste en la formación de imágenes invertidas. Se observa en regiones de clima cálido principalmente y se debe a un efecto de reflexión total.
Las capas de aire en contacto con la Tierra, caldeada por el Sol, se calientan extremadamente, y el aire se dispone por capas en orden creciente de densidades de abajo hacia arriba, de modo que las capas más densas están arriba. Esto sucede en días de calma , durante cierto tiempo. En estas condiciones, los rayos de luz que parten del objeto sufren sucesivas refracciones en capas de aire cada vez menos refringente, y llegará el momento en que el ángulo de incidencia sea mayor que el ángulo límite y origine la reflexión total. El objeto se verá invertido, como si se reflejará en el agua de un lago. Esta ilusión se tiene también a veces en los días cálidos en caminos y campos, así como en carreteras asfaltadas, que dan la impresión de que están cubiertas de agua que refleja el cielo. Son capas calientes de aire que reflejan la luz como si fueran un espejo.
-
Lentes
-
Concepto
Se llama lente a un medio transparente limitado por caras curvas o por una plana y otra curva.
Clasificación de las lentes
Lentes convergentes o positivos
Lentes divergentes o negativos
Lente, en sistemas ópticos, disco de vidrio u otra sustancia transparente cuya forma hace que refracte la luz procedente de un objeto y forme una imagen real o virtual de éste. Las lentes de contacto o las lentes de las gafas o anteojos corrigen defectos visuales. También se utilizan lentes en la cámara fotográfica, el microscopio, el telescopio y otros instrumentos ópticos. Otros sistemas pueden emplearse eficazmente como lentes en otras regiones del espectro electromagnético, como ocurre con las lentes magnéticas usadas en los microscopios electrónicos. (En lo relativo al diseño y uso de las lentes. En lo relativo a la lente del ojo).
Las lentes con superficies de radios de curvatura pequeños tienen distancias focales cortas. Una lente con dos superficies convexas siempre refractará los rayos paralelos al eje óptico de forma que converjan en un foco situado en el lado de la lente opuesto al objeto. Una superficie de lente cóncava desvía los rayos incidentes paralelos al eje de forma divergente; a no ser que la segunda superficie sea convexa y tenga una curvatura mayor que la primera, los rayos divergen al salir de la lente, y parecen provenir de un punto situado en el mismo lado de la lente que el objeto. Estas lentes sólo forman imágenes virtuales, reducidas y no invertidas.
Si la distancia del objeto es mayor que la distancia focal, una lente convergente forma una imagen real e invertida. Si el objeto está lo bastante alejado, la imagen será más pequeña que el objeto. Si la distancia del objeto es menor que la distancia focal de la lente, la imagen será virtual, mayor que el objeto y no invertida. En ese caso, el observador estará utilizando la lente como una lupa o microscopio simple. El ángulo que forma en el ojo esta imagen virtual aumentada (es decir, su dimensión angular aparente) es mayor que el ángulo que formaría el objeto si se encontrara a la distancia normal de visión. La relación de estos dos ángulos es la potencia de aumento de la lente. Una lente con una distancia focal más corta crearía una imagen virtual que formaría un ángulo mayor, por lo que su potencia de aumento sería mayor. La potencia de aumento de un sistema óptico indica cuánto parece acercar el objeto al ojo, y es diferente del aumento lateral de una cámara o telescopio, por ejemplo, donde la relación entre las dimensiones reales de la imagen real y las del objeto aumenta según aumenta la distancia focal.
La cantidad de luz que puede admitir una lente aumenta con su diámetro. Como la superficie que ocupa una imagen es proporcional al cuadrado de la distancia focal de la lente, la intensidad luminosa de la superficie de la imagen es directamente proporcional al diámetro de la lente e inversamente proporcional al cuadrado de la distancia focal. Por ejemplo, la imagen producida por una lente de 3 cm de diámetro y una distancia focal de 20 cm sería cuatro veces menos luminosa que la formada por una lente del mismo diámetro con una distancia focal de 10 cm. La relación entre la distancia focal y el diámetro efectivo de una lente es su relación focal, llamada también número f. Su inversa se conoce como abertura relativa. Dos lentes con la misma abertura relativa tienen la misma luminosidad, independientemente de sus diámetros y distancias focales.
Fabricación de Lentes
La mayoría de las lentes están hechas de variedades especiales de vidrio de alta calidad, conocidas como vidrios ópticos, libres de tensiones internas, burbujas y otras imperfecciones. El proceso de fabricación de una lente a partir de un bloque de vidrio óptico implica varias operaciones. El primer paso consiste en serrar una lente en bruto a partir del bloque de vidrio. Para ello se presiona el vidrio contra una delgada placa metálica circular que se hace girar. El borde de la placa se carga con polvo de diamante. Después, se le da una primera forma a la pieza en bruto prepulimentándola sobre una placa plana de hierro colado cubierta con una mezcla de granos abrasivos y agua. Para formar la superficie redondeada de la lente se la talla con herramientas cóncavas o convexas cargadas con abrasivos. La superficie de una lente convexa se forma mediante una herramienta cóncava y viceversa. Generalmente se emplean dos o más herramientas en este proceso de tallado, utilizando grados de abrasivo cada vez más finos. El último proceso de acabado de la superficie de la lente es el pulido, que se realiza mediante una herramienta de hierro cubierta de brea y bañada con mordiente rojo y agua. Tras el pulido, la lente se 'remata' rectificando el borde hasta que el centro físico coincida con su centro óptico (el centro óptico es un punto tal que cualquier rayo luminoso que pasa por él no sufre desviación). Durante este proceso se coloca la lente en el bastidor de un torno, de forma que su centro óptico se encuentre en el eje de giro, y se rectifican los bordes con una tira de latón cargada con abrasivo.
Caracterización de las Lentes
Las características ópticas de las lentes sencillas (únicas) o compuestas (sistemas de lentes que contienen dos o más elementos individuales) vienen determinadas por dos factores: la distancia focal de la lente y la relación entre la distancia focal y el diámetro de la lente. La distancia focal de una lente es la distancia del centro de la lente a la imagen que forma de un objeto situado a distancia infinita. La distancia focal se mide de dos formas: en unidades de longitud normales, como por ejemplo 20 cm o 1 m, o en unidades llamadas dioptrías, que corresponden al inverso de la distancia focal medida en metros. Por ejemplo, una lente de 1 dioptría tiene una distancia focal de 1 m, y una de 2 dioptrías tiene una distancia focal de 0,5 m. La relación entre la distancia focal y el diámetro de una lente determina su capacidad para recoger luz, o "luminosidad". Esta relación se conoce como número f, y su inversa es la abertura relativa.
Historia
Las primeras lentes, que ya conocían los griegos y romanos, eran esferas de vidrio llenas de agua. Estas lentes rellenas de agua se empleaban para encender fuego. En la antigüedad clásica no se conocían las auténticas lentes de vidrio; posiblemente se fabricaron por primera vez en Europa a finales del siglo XIII. Los procesos empleados en la fabricación de lentes no han cambiado demasiado desde la edad media, salvo el empleo de brea para el pulido, que introdujo Isaac Newton.
El reciente desarrollo de los plásticos y de procesos especiales para moldearlos ha supuesto un uso cada vez mayor de estos materiales en la fabricación de lentes. Las lentes de plástico son más baratas, más ligeras y menos frágiles que las de vidrio.
-
Tipos de Lentes
Clasificación de las Lentes Convergentes y Divergentes
Las lentes convergentes tienen el espesor de su parte media mayor que el de su parte marginal.
Las lentes divergentes son más delgadas en el centro que en los bordes.
Biconvexa o convergente.
Plano convexa.
Menisco convergente.
Bicóncava.
Plano cóncava.
Menisco divergente.
Elementos de una Lente
Centro Óptico, donde todo rayo pasa por él, no sufre desviación.
Eje Principal, es la recta que pasa por los centros de curvatura.
Foco Principal, punto en donde pasan los rayos que son paralelos.
Eje Secundario, es la recta que pasa por el centro óptico.
Rayos notables en las lentes convergentes
Rayo paralelo al eje principal se refracta y pasa por el foco.
El rayo que pasa por el foco principal es decir el rayo emergente que la corresponde es paralelo al eje principal.
Todo rayo que pase por el centro óptico no sufre desviación.
-
Formación de Imágenes en las Lentes
Construcción gráfica de imágenes en las lentes convergentes
-
Imágenes reales, son aquellas capaces de ser recibidas sobre una pantalla ubicada en tal forma de que entre ella y el objeto quede la lente.
-
Imagen virtual, está dada por la prolongación de los rayos refractados, no se puede recibir la imagen en una pantalla.
El objeto está a una distancia doble de la distancia focal. La imagen obtenida es: real, invertida, de igual tamaño, y también a distancia doble de la focal.
El objeto está a distancia mayor que el doble de la distancia focal. Resulta una imagen: real invertida, menor, formada a distancia menor que el objeto.
El objeto está entre el foco y el doble de la distancia focal. La imagen obtenida es: real invertida, mayor, y se forma a mayor distancia que el doble de la focal.
El objeto está entre el foco y el centro óptico. Se obtiene una imagen: virtual, mayor, derecha, formada del lado donde se coloca el objeto.
El objeto está en el foco principal, no se obtiene ninguna imagen.
Lente convexa
Una lente convexa es más gruesa en el centro que en los extremos. La luz que atraviesa una lente convexa se desvía hacia dentro (converge). Esto hace que se forme una imagen del objeto en una pantalla situada al otro lado de la lente. La imagen está enfocada si la pantalla se coloca a una distancia determinada, que depende de la distancia del objeto y del foco de la lente. La lente del ojo humano es convexa, y además puede cambiar de forma para enfocar objetos a distintas distancias. La lente se hace más gruesa al mirar objetos cercanos y más delgada al mirar objetos lejanos. A veces, los músculos del ojo no pueden enfocar la luz sobre la retina, la pantalla del globo ocular. Si la imagen de los objetos cercanos se forma detrás de la retina, se dice que existe hipermetropía.
Fórmula de los focos conjugados de las lentes convergentes
| 1 | = | 1 | + | 1 | x | (imágenes reales) |
| f | d | d' | ||||
| x | ||||||
| 1 | = | 1 | - | 1 | (imágenes virtuales) | |
| F | d | d' |
f = distancia focal
d = distancia del objeto
d' = distancia donde se obtiene la imagen
Lentes Divergentes
En las lentes divergentes las imágenes siempre resultan virtuales, de igual sentido y situados entre la lente y el objeto.
Lentes divergentes
Fórmula
| - | 1 | = | 1 | - | 1 |
| f | D | d' |
Lente cóncava
Las lentes cóncavas están curvadas hacia dentro. La luz que atraviesa una lente cóncava se desvía hacia fuera (diverge). A diferencia de las lentes convexas, que producen imágenes reales, las cóncavas sólo producen imágenes virtuales, es decir, imágenes de las que parecen proceder los rayos de luz. En este caso es una imagen más pequeña situada delante del objeto (el trébol). En las gafas o anteojos para miopes, las lentes cóncavas hacen que los ojos formen una imagen nítida en la retina y no delante de ella.
Potencia de una Lente
Dioptría
Potencia de una lente es la a la inversa de su distancia focal.
Potencia = 1/foco P = 1/m =una dioptría.
La potencia de una lente es la reciproca de su distancia focal.
Problema
Calcular en dioptrías las potencias de las siguientes lentes:
a) f = 2 m b) f = 25 cm c) f = -40 cm
Solución
| a) | p = | 1 | = | 1 | = | 0.5 dioptrías |
| f | 2 m | |||||
| x | ||||||
| b) | p = | 1 | = | 1 | = | 4 dioptrías |
| f | 0.25 m | |||||
| X | ||||||
| c) | p = | 1 | = | 1 | = | -2.5 dioptrías |
| f | 0.4 m |
Fórmula para calcular el aumento o relación entre el tamaño de la imagen y el objeto
| i | = | d' | XXXXX | i = imagen |
| o | d | o = objeto | ||
| d = distancia de la lente al objeto | ||||
| d' = distancia de la lente a la imagen |
Problema
a) ¿Cuál es la posición de la imagen que brinda una lente convergente cuya distancia focal es de 40 cm, colocado el objeto a 55 cm de ella?
| Datos | X | Fórmula | X | Despejando | X | Sustitución | X |
| F = 40 cm | 1 | = | 1 | + | 1 | 1 | = | 1 | - | 1 | 1 | = | 1 | - | 1 | d' = | 440 cm |
| d = 55 cm | f | d | d' | d' | f | d | d' | 40 cm | 55 cm | 3 |
| d' = ? | |
| Enviado por: | Beelzebú |
| Idioma: | castellano |
| País: | México |