Matemáticas
Radicales
TEORÍA DE EXPONENTES Y RADICALES
TEORÍA DE RADICALES
![]()
Signo del radical
INDICE Cantidad subradicalo
RADICANDO
![]()
LEYES
![]()
-
![]()
-
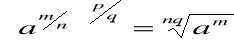
-
-
![]()
![]()
-
-
EJERCICIOS
Hallar el valor numérico de las siguientes expresiones:
![]()
![]()
![]()
![]()
![]()
![]()
CALCULAR: la raíz cuadrada y cúbica de los siguientes números.
![]()
![]()
Hallar el valor numérico de las siguientes expresiones o simplifíquela.
![]()
![]()

EJERCICIOS

![]()
![]()
![]()
EXTRACCIONES DE FACTORES DE UN RADICAL
![]()
![]()
![]()
Si el radicando contiene uno o más factores que sean potencias de exponente igual al índice del radical, estos factores pueden extraerse del radical (como factores) las bases de dichas potencias.
SIMPLIFICANDO LAS SIGUIENTES RADICALES
POR EXTRACCIÓN DE FACTORES
![]()
![]()
![]()
![]()
![]()
![]()
RACIONALIZACIÓN
Sin un radical afecta a una expresión fraccionaria o, si en el denominador de una fracción hay algún radical se llama: RACIONALIZACIÓN de una expresión al procedimiento mediante el cual se logra que no este afectado por radical alguno.

EJEMPLOS
ADICIÓN Y SUSTRACCIÓN DE RADICALES
Que son radicales semejantes:
2 términos que contengan cada uno un radical como factor, se dicen semejantes, cuando estas radicales tienen el mismo índice y el mismo radical.
La semejanza de los monomios se establecen atendiendo al radical que contienen y presidiendo del carácter de los demás factores.
ADICIÓN
Una suma algebraica de términos que contengan radicales puede reducirse aun monomio siempre que se trate de términos semejantes; pues hasta entonces se aplica la propiedad distributiva sacando factor común el radical.
Como coeficiente de la suma resultará la correspondiente sima algebraica de los factores exteriores a los radicales en los diversos términos.
![]()
Ejercicios
![]()
![]()
![]()
REDUCCIÓN DE RADICALES A OTROS EQUIVALENTES
REDUCCIÓN DE RADICALES A UN ÍNDICE COMÚN
Teniendo en cuenta que es fácil reducir varios radicales a otros que tengan el mismo índice pues hasta multiplicar cada índice y el exponente de la cantidad subrradical por el número apropiado.
La reducción de radicales de un índice común es utilizar en la multiplicación y en la división de expresiones con radicales; también se aplica esta operación cuando se trata de comparar numéricamente varios radicales sin hacer las correspondientes extracciones de raíces. Reducir los radicales siguientes a otros equivalentes del mismo índice.
![]()
m. c. i.= 12
![]()
MULTIPLICACIÓN DE RADICALES
MONOMIOS
Si las expresiones dadas contienen radicales del mismo índice, se halla el producto de los coeficientes; en la forma usual y para multiplicar los radicales se tiene en cuenta que el producto de dos radicales del mismo índice es otro radical de igual índice cuyo radicando es el producto de los radicandos de los factores.
![]()
![]()
![]()
Polinomios
Para multiplicar dos expresiones polinómicas que contengan radicales, se produce como en la multiplicación de dos polinomios cualquiera.
![]()
![]()
![]()
División de radicales
Monomios
![]()
Si las expresiones dadas contienen radicales del mismo índice dividen los coeficientes de los radicales en forma usual.

Polinomios. - el coeficiente de dos expresiones polinómicas, cuyos términos contengan radicales, pueden expresarse en forma entera, con respecto a los radicales mediante la racionalización del denominador.
Si el denominador fuese de forma a-b se racionalizaran entonces multiplicando por la suma a+b

![]()
![]()
ECUACIONES DE SEGUNDO GRADO

Se llaman ecuaciones algebraicas de segundo grado o ecuaciones cuadráticas.
ECUACIONES INCOMPLETAS DE SEGUNDO GRADO
ECUACIÓN DE LA FORMA ax2 +c
ECUACIÓN DE LA FORMA x2 = 2x
ECUACIÓN DE LA FORMA ax2+bx=0
ECUACIÓN DE LA FORMA AX2= 0


Sabemos que una ecuación incompleta de la forma ax2+bx = 0 se resuelve sacando x como factor común cuando se tiene una ecuación incompleta de la forma ax2+bx+c=0 y el trinomio que forma el primer miembro de la ecuación puede descomponerse por algunos métodos estudiados anteriormente, la resolución de la ecuación de segundo grado queda reducida así a la resolución de 2 ecuaciones simples de 1er grado.
Ejercicios


Solución
RESOLUCIÓN POR EL MÉTODO DE COMPLETAR UN CUADRADO PERFECTO
Puesto que:

A un binomio de la forma x2+mx con m positivo o negativo le falta el cuadrado de la mitad de m, o sea el término:
![]()
Para ser un cuadrado perfecto por ejemplo ax2+8x falta agregable


Sumando el 9 en ambos miembros tenemos:
X2 +6x + 9= 7+5
Si extraemos la raíz cuadrada en ambos miembros tenemos:

PROGRESIONES ARITMÉTICAS
Término n-s+ mo de una progresión aritmética a, a+d, a dd, a+3d…. a+(n-1)d
Un= a + (n-1)d
N= K
UK= a+(k-d)d
Sumando d en ambos miembros
Uk+d= a+(k-1)d+d
Uk+d= a+kd-d+d
Uk+d=a+kd
Ésta formula es válida para nk+1 para n=k-1 se obtiene en una progresión.
a= 4
d= 3
U7= 4+(7-1)3
U7= 22 es el séptimo término
EJERCICIOS

![]()
8 Término

Una progresión aritmética se compone de 50 términos si el 1er es 9 su diferencia es -3.

Una progresión aritmética se compone de 20 términos la diferencia es -0.75 cual será 1er término.


MEDIOS ARITMÉTICOS

INTERPOLAR

18, 15, 12, 9, 6, 3, 0, -3, -6, -9

seis medios aritméticos entre 3 y 8
Interpolar 3 y 8
3, 8, 13, 18, 23, 28, 33…………

![]()
Ejercicios

9° Término de 7, 10, 13
25° Término de -6, -3

PROGRESIONES GEOMÉTRICAS
Es una progresión cuyos términos son tales que van a cualquiera de ellos, después de el 1ro, es igual al término anterior multiplicando por un número fijo que le puede hallar dividendo cualquier término de la progresión y se representa por la letra r.
Ejemplos
2, 6, 18…..
Es una progresión creciente cuya razón es r = 3
8, -4,2
Es una progresión decreciente cuya razón es r = ½
LOGARITMOS
El logaritmo de un número es el exponente a que hay que elevar una base positiva y distinta a la unidad. Para obtener una potencia igual al número dado.
El logaritmo es, por tanto, una de las operaciones inversas de la potenciación. Por la definición de logaritmo vemos que la base puede ser cualquier número positivo diferente de la unidad pero en la practica se han elegido 2 bases debido a la simplificación de cálculos que su elección lleva consigo, estas son la base de 10 y la base.
Los logaritmos de base 10 se conocen como decimales o vulgares y los logaritmos de base e se conocen como NEPERIANOS
PROPIEDADES DE LA FUNCIÓN EXPONENCIAL
La función exponencial es siempre más para todos los valores de x es decir, el gráfico se mantiene siempre x arriba del eje horizontal.
A cad valor de x corresponde a un solo valore de (y) y cda coordenada corresponde al valor de x.
Cualquiera que sea la base a = o, la función toma un valor 1 para x= 0. Esto es todos los gráficos pasan por el punto (0,1)
Si > 1 la función exponencial es creciente, es decir, las ordenadas, crecen al crecer las obscisas por lo contrario si o<a<1 la función es decreciente.
CÁLCULO CON POTENCIA DE 10
Los números decimales se pueden expresar en notación científica mediante el uso de potencias de 10 con exponentes enteros. Ej.
Si en vez de expresar parcialmente los # como potencias de 10 los expresaremos completamente en esa forma mediante tablas que se han construido expresamente con ese objeto.
Por tanto: (5, 24, 10) (3,5. 103)= 101, 7, 9 3 9 3 X 10359407
=105 2 6 3 4 8
= 100 2 6 3 4 0 X 105
Haciendo de nuevo uso de la tabla para encontrar el valor de 100126340, hablamos 1834
Luego en definitivo
Logaritmos
Dando Como base un # a + y diferente de 1 se llama logaritmo de un número real y + n, con respecto a dicha base, al exponente x al cual se debe elevar la base a para obtener el número N.
Esto es si
ax = N
Diremos que x es el logaritmo de N en base a y con respecto a la base, lo cual se debe elevar la base a para obtener el # N
Esto es si
Ax=N
Diremos que x es el logaritmo de N en base
x= loga N
Ejemplo
1. Puesto que 43= 64, diremos que el logaritmo de 64 en base 4 es 3
log4 64 = 3
PROPIEDADES DE LOS LOGARITMOS
Además de las propiedades generales mencionadas apartado anterior, los logaritmos poseen otras propiedades importantes que sirven de base al cálculo con logaritmos.
Como estas propiedades son consecuencias de leyes de los exponentes y son ciertas cualquiera sea la base.
Ejemplo
- El logaritmo de la base es siempre 1
- El logaritmo de 1 es siempre 0, cualquiera que sea la base
a2= 1 loga 1=0
- El logaritmo de un producto es igual a la suma de los logaritmos de sus factores.
- Esta igualdad demuestra que m + n es el logaritmo en base a del producto MN loga MN= m+n= loga M+loga N
- El logaritmo de un cociente es igual a la diferencia entre el logaritmo del dividendo y el logaritmo del divisor.
- El logaritmo es una potencia es = al producto del exponente por el logaritmo de la base de la potencia
loga mk = k loga M.
- El logaritmo de una raíz es igual al logaritmo del radicando dividido por el índice del radical.
![]()
No existen reglas simples que expresan
Si M y N toman valores numéricos para calcular (MIN) se compensará por ejecutar la suma o diferencia M=N
ESTADÍSTICA
Problemas fundamentales. - se llama estadística a la recopilación ordenado de datos numéricos sobre asuntos determinados.
Por ejemplo:
Cuando hablamos de la población del país al determinar el número de habitantes por: provincia, sexo, edad, nivel académico, nivel socioeconómico, etc.
OBJETIVOS DE LA ESTADÍSTICA
Tienen los siguientes.
Clasificar, reordenar y representar gráficamente el conjunto de los datos obtenidos, en una forma fácil y precisa los hechos más importantes significativos la estadística moderna va más allá de este proceso de reducción, análisis y representación apropiada de los datos coleccionados.
Predecir las condiciones futuras mediante el conocimiento de las condiciones pasadas y presentes.
lograr información sobre una gran masa de hechos.
DISTRIBUCIONES
Es analizar si los datos se disponen en orden de magnitud numérica e indicando el número de valores que caen en ciertas categorías o clases, se obtiene una distribución de una frecuencia.
Distribución de frecuencia
Es la disposición de los datos en clase especificando el número de datos y observaciones de cada clase. Una tabla de frecuencia es una presentación en una forma tabular de un distribución de una frecuencia.
Ejemplo. - Un biólogo mide 20 ejemplares de cierta especie de insectos y obtienen los siguientes valores (en cm)
2,7; 3,1; 2,3; 3,4; 3,6; 2,9; 2,4; 2,8; 3,7; 3,2; 2,5; 3,3; 3,1; 2,6; 2,8; 3,0; 3,4; 3,9; 2,7.
Los insectos tienen una longitud mayor de 2 cm. pero menos 4 cm. Si dividimos este intervalo en 4 partes, cada uno de 0,5 cm de longitud y los datos en forma creciente de magnitud y distribuidas.
Entre 2 y 2,5 - cm.: 2,3; 2,4
Entre 2,5 y 3 - cm.: 2,5; 2,6; 2,7; 2,8; 2,9
Entre 3 y 3,5 - cm.: 3,0; 3,1; 3,2; 3,3; 3,4; 3,2; 3,4;
Entre 3,5 y 4 - cm.: 3,6; 3,7; 3,9;
Con estos datos se contribuye la siguiente tabla de frecuencia.
| Longitud (en Cm) | # de insectos (frecuencia |
| 2 - 2, 5 2,5 - 3 3 - 3,5 3,5 - 4 | 2 7 8 3 |
En esta tabla se nota que el 75% de los insectos observados, su longitud es de 2,5 y 3,5 cm.
Ejemplo
La tabla II muestra las calificaciones de un grupo de estudiantes de álgebra, la tabla III de las estaturas de un de hombres.
TABLA II
| CALIFICACIONES | FRECUENCIA |
| 00-10 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 90 - 100 | 2 3 5 6 9 11 15 18 14 8 |
Calificaciones recibidas por una clase de álgebra
Tabla III
| ESTATURA EN PULGADAS | FRECUENCIA |
| 56 - 58 58 - 60 60 - 62 62 - 64 64 - 66 66 - 68 68 - 70 70 - 72 72 - 74 74 - 76 | 5 7 10 18 82 170 113 60 27 8 |
Estaturas de 500 hombres
PROMEDIOS
Los datos estadísticos a agruparse alrededor de un cierto valor produciendo un punto más alto que los demás en lo que corresponde a la curva de frecuencia lo cual el lector en varios de los ejemplos anteriores habrá observado.
Todo valor que se utilice para la distribución de frecuencias y en general, una serie estadística cualquiera, recibe el nombre de promedio.
Los promedios de dos distribuciones pueden usarse para sacar una comparación entre ellas.
Los tipos más importantes de promedio son los siguientes: la medida aritmética, la medicina, el modo, la media geométrica y la media cuadrática
Antes de definir estos promedios y buscar la manera de obtenerlos nos conviene recordar el uso del símbolo ( Enigma) ya introducido para indicar abreviadamente la suma de varios términos del mismo tipo. Así, por ejemplo la suma: x1+x2+x3+x4+x5+x6
Se representa abreviadamente escribiendo
![]()
La notación indica que el primer valor que debe darse el símbolo r es 1 y el último es 6
Análogamente
![]()
Significa a1+ a2+a3+a4
![]()
En general
X1 + x2 + x3 …….. + xn
Sin embargo cuando se trata de sumar de términos de la forma escribiremos simplemente para representarlo, omitiendo la indicación de los valores extremos del subíndice.
Como ejemplo y por su aplicación anterior demostraremos las dos propiedades siguientes:
![]()
1.
![]()
2.
LA MEDIA ARITMÉTICA
Este es el promedio más conocido y más comúnmente usado. Su determinación es simple aunque puede resultar cuando los datos son numerosos. También puede ser afectada por valores extremos desusados y puede dejar de ser un valor realmente típico o representativo de la distribución.
Cuando cada uno de los valores (extremos) con la frecuencia fr, la formula (1) se escribe

Ejemplo
La medida aritmética de las calificaciones de la tabla II se halla de la manera siguiente:
| Valores | Frecuencia | Xr fr |
| 5 15 25 35 45 55 65 75 85 95 | 2 3 5 6 9 11 15 18 14 8 | 10 45 125 210 405 605 975 1350 1190 760 |
| Sumas | 91 | 5675 |
De donde
![]()
El computo anterior se puede abreviar aún más escogiendo un origen arbitrario (llamado también promedio hipotético o supuesto) y procedimientos a calcular por medio de la formula
![]()
En lo cual dr representa la diferencia Xr o desviaciones con respecto al promedio supuesto
Cuando la formula (3) se aplica a una distribución de frecuencias se escribe

Para aplicar esta formula al calculo de la media aritmética de las calificaciones de la tabla II prepararemos, eligiendo por ejemplo A= ss, la siguiente tabla
| dr | Fr | dr fr. |
| -50 -40 -30 -20 -10 0 10 20 30 40 | 2 3 5 6 9 11 15 18 14 8 | -100 -120 -150 -120 -90 0 150 360 420 320 |
| Total | 91 | 670 |
De donde 670: 91 = 7.4
Luego x=55+7,4=62.4

![]()
Se abrevia algo más los cálculos escribiendo la formula
En donde h es la amplitud de intervalo de clase y dr.= dr/h: en algunos casos se asigna un # arbitrario Wr, llamado pese, a cada xr, se define entonces la media ponderada o barica. W de los valores x1 + x2 xn por medio de la formula.
La Mediana
La mediana de un conjunto de valore x1, x2, Xn dispuestos en orden creciente o decreciente es el valor equidistante de los extremos, cuando n es impar, si n es par se forma como mediana aritmética de los valores centrales.
Ejemplo
La mediana de 22, 23, 25, 28, 30 es 25
La mediana de 40, 43, 45, 46, 48, 51, es 12=45.5
Si los datos se han dispuesto en forma de una distribución de frecuencias, la mediana se define como la obscisa cuyo correspondiente ordenada divide el área del histograma en 2 partes equivalentes.
El modo
Es el valor que se presenta con mayor frecuencia en la serie estadística cuando hay varios valores con frecuencias máximas el modo queda indeterminado.
En la distribución de ka tabla II la clase modal es la que corresponde al intervalo o sea 75
En la distribución de la tabla III el modo daría aproximadamente 67.
La medida Geométrica
La medida geométrica de n valores x1, x2……xn se define mediante la formula
Tomando logaritmos se puede escribir en la forma
En donde se ve que el logaritmo de la media Geométrica de n cantidades en la media aritmética de los logaritmos de estas cantidades.
Ejemplo
Hallar la media de 2, 3, 7 y 15
Tenemos: Log. 2 - 0,30103
Log. 3 - 0,47713
Log. 7 - 0,84510
Log. 15- 1,17609
2,79934
![]()
luego:
6=5,01
![]()
pero de B = Arm se obtiene
y sustituyendo en [9]
Por tanto para determinar P (dentro de la hipótesis hecha) habrá que tomar la medida geométrica de las poblaciones dadas por los dos censos.
LA MEDIDA ARITMÉTICA
![]()
La medida aritmética x de n valores x1, x2….xn se define
Con la presente formula podemos calcular medias aritméticas simples.
Mientras que cuando uno de los valores Xr. Ocurre con la frecuencia fr, la formula es la siguiente:

La presente formula sirve si los datos de han dispuesto en forma de distribución de frecuencia, el cálculo de la media aritmética se la hace abreviando tomando en cuenta a x r como los puntos medios de los intervalos y como fr las frecuencias correspondientes a las respectivas clases. Ejem.
La media aritmética se las calificaciones de la tabla.
| Valores centrales | frecuencias | xr fr |
| 5 15 25 35 45 55 65 75 85 95 | 2 3 5 6 9 11 15 18 14 8 | 10 45 125 210 405 605 975 1350 1190 760 |
| total | 91 | 5675 |
De donde ![]()
La media aritmética se calcula con los datos distribuidos uniformemente dentro de cada intervalo de clase y que en consecuencia los puntos medios de las clases son valores típicos para cada intervalo.
Se puede abreviar esta formula tomando en cuenta el origen arbitrario y llamado también promedio hipotético y procedimiento a calcular.

Desviaciones con respecto al promedio supuesto
![]()
Si quieres aplicar la formula a una distribución de frecuencias se escribe de la siguiente manera

Para aplicar esta formula. Ejemplo
| xr | dr | fr | dr fr |
| 5 15 25 35 45 55 65 75 85 95 | -50 -40 -30 -20 -10 0 10 20 30 40 | 3 3 5 6 9 11 15 18 14 8 | -100 -120 -150 -120 -90 0 150 360 420 320 |
| Total | 91 | 670 |
![]()
De donde
![]()
Luego
La formula 4 la podemos abreviar tomando en cuenta

n: es la amplitud del intervalo de clase
![]()
dr: a la diferencia
En el ejemplo anterior h es = 10
Por otra parte puede ser probablemente afectada por valores extremos desusados y pueden dejar de ser un valor realmente típico.
Ejemplo
La media aritmética de las calificaciones
La mediana
Para determinar numéricamente el valor de la mediana se construye una tabla acumulativa de frecuencia y se halla el valor de x correspondiente a la frecuencia acumulada igual a la mitad de la frecuencia total
n= f1 + f2 + ………..fn
en muchos casos la mediana es un promedio más típico que otro a causa de su independencia de valores anormales que pueden ocurrir en la serie estadística.
El modo
El valor que se presenta con mayor frecuencia es la serie cuando hay varios valores con frecuencia en la serie estadística, cuando hay varios valores con frecuencia máxima el modo.
Ejemplo
Calcular la mediana de los siguientes datos de 650 personas
| Años | fr | fa | M fa | |
| 0-5 5-10 10-15 15-20 20-25 25-30 30-35 35-40 40-45 45-50 50-55 55-60 | 20 25 40 60 80 10 35 100 70 50 70 90 | 20 45 85 145 225 235 270 370 440 490 560 650 | 325 |
![]()
![]()
![]()
| Intervalos | fr | fa | M fa | d |
| 100-150 150-200 200-250 250-300 300-350 350-400 400-450 450-500 500-550 550-600 600-650 | 20 30 10 40 70 80 100 75 25 105 140 | 20 50 60 100 19 27 370 445 470 575 715 | 357,5 | 87,5 |
![]()

![]()
| Edad | fr | fa | M fa | d |
| 42-44 44-46 46-48 48-50 50-52 52-54 54-56 56-58 58-60 60-62 | 5 8 9 11 15 5 20 10 12 13 | 5 13 22 33 48 51 71 81 93 106 | 53 | 2 |
![]()
![]()
![]()
![]()
![]()


![]()
![]()
Descargar
| Enviado por: | Djorge |
| Idioma: | castellano |
| País: | Ecuador |
