Matemáticas
Radicales y raíces
RADICALES
Se llama raíz n-ésima de un número a, y se escribe ![]()
, a un número b que elevado a n dé a.
Ejemplos:
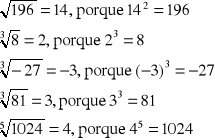
![]()
se llama radical; a, radicando; y n, índice de la raíz.
EXISTENCIA DE RADICALES.
Primera: si a es positivo, ![]()
existe, cualquiera que sea n.
![]()
Segunda: si a es negativo, sólo existen sus raíces de índice impar.
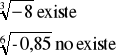
Tercera: salvo que a sea una potencia n-ésima de un número entero o fraccionario,![]()
es un número irracional. Sólo podremos obtener su expresión decimal aproximada.
FORMA EXPONENCIAL DE LOS RADICALES
La raíz n-ésima de un número puede ponerse en forma de potencia:
![]()
Esta nomenclatura es coherente con la definición.
![]()
Es importante familiarizarse con la forma exponencial de los radicales, pues nos permitirá expresarlos y operar cómodamente con ellos.
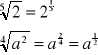
PROPIEDADES DE LOS RADICALES
Los radicales tienen una serie de propiedades, que debemos conocer y utilizar con soltura. Todas ellas son consecuencia inmediata de conocidas propiedades de las potencias. Veámoslas una a una, estudiando su significado en algunos ejemplos, y viendo sus aplicaciones.
Primera:
![]()
Ejemplos:

Esta propiedad tiene dos importantes aplicaciones:
simplificar radicales tal y como se ha visto en los ejemplos anteriores;
conseguir que dos o más radicales tengan el mismo índice (reducir a índice
común).

Segunda:
![]()
Ejemplos:

Esta propiedad tiene dos aplicaciones importantes:
sacar un factor fuera de la raíz;

de modo contrario, juntar varios radicales en uno solo.
![]()
Tercera:

Ejemplos:

Esta propiedad, junto con la primera y segunda, sirve para poner productos y cocientes de radicales bajo una sola raíz.

Cuarta:
![]()
Ejemplos:
![]()
Quinta:
![]()
Ejemplos:

RADICALES SEMEJANTES
Dos radicales son semejantes cuando tienen el mismo índice y radicando.
Los radicales![]()
y ![]()
son semejantes. Tienen el mismo índice, 2, y el mismo radicando, 3.
![]()
y ![]()
son semejantes. Esto se comprueba sacando factores del radical.
![]()
y![]()
son semejantes. Esto se comprueba sacando factores del radical.

Más ejemplos de radicales semejantes:

OPERACIONES CON RADICALES
La suma o la resta de radicales semejantes es otro radical semejante a los dados, cuyo coeficiente es igual a la suma o la resta de los coeficientes de los radicales sumados o restados.
![]()
Ejemplo:
![]()
Si los radicales no son semejantes, la suma se deja indicada.
Ejemplo:
![]()
El producto de radicales, con el mismo índice, es igual a otro radical cuyo coeficiente y radicando son iguales, respectivamente, a los productos de los coeficientes y radicandos de los factores.
![]()
Ejemplo:
![]()
El cociente de dos radicales con el mismo índice, es igual a otro radical, cuyo coeficiente y radicando son iguales, respectivamente, al cociente de los coeficientes y radicandos de los radicales dividendo y divisor.

Ejemplo:
![]()
La potencia de un radical es igual a otro radical, cuyo coeficiente y radicando están elevados a dicha potencia.
![]()
Ejemplo:
![]()
Es importante observar que al elevar al cuadrado un radical de índice 2, se obtiene el radicando.
![]()
Ejemplo:
![]()
EXPRESIONES FRACCIONARIAS
Al efectuar cálculos con radicales pueden surgir expresiones fraccionarias en las que aparezcan radicales.
Estas expresiones no son números racionales, pues para ello el numerador y el denominador tendrían que ser números enteros.
A estas expresiones las llamaremos expresiones fraccionarias, y verifican las mismas propiedades que los números racionales. Es especialmente importante recordar estas dos:
Primera: dos expresiones fraccionarias son equivalentes si los productos cruzados son iguales.
Segunda: si multiplicamos el numerador y el denominador de una expresión fraccionaria por una misma expresión distinta de cero, se obtiene una expresión fraccionaria equivalente a la primera.
Conclusión
Muchas personas encuentran las matemáticas un tema arduo, complicado y, a veces, indescifrable. Por eso, en esta carpeta hemos tratado de huir de formalismos, que en ocasiones consiguen desviar y hemos ejemplificado todas las definiciones
Las bases de las matemáticas no es saber mucho, sino saber hacer.
Bibliografía
Enciclopedia aritmética
Editorial el periódico
Enciclopedia temática interactiva matemática
Ediciones I y II
Lectus Vergara
Zeta Multimedia
9
Descargar
| Enviado por: | Die |
| Idioma: | castellano |
| País: | Chile |
