Ingeniero de Caminos
Propagación de errores
EXPERIMENTO Nº 2
PROPAGACIÓN DE ERRORES
INTRODUCCIÓN
Para la física y la química en su calidad de ciencias experimentales, la medida constituye una operación fundamental. Sus descripciones del mundo físico se refieren a magnitudes o propiedades susceptibles de ser medidas. Las unidades, como cantidades de referencia a efectos de comparación, forman parte de los resultados de las medidas. Cada dato experimental se acompaña de su error o, al menos, se escriben sus cifras de tal modo que reflejan la precisión de la correspondiente medición.
Una de las labores más importantes en el laboratorio es la medición, el ser precisos al momento de expresar el tamaño de un objeto puede ser la diferencia entre el éxito o el fracaso de un experimento. Con mucha frecuencia es necesario expresar longitudes en términos de unidades que contienen decimales, y estos están dados por los decimales que contiene la regla usada para medir, sin embargo a veces es necesario una medición más precisa, en esos casos se usan instrumentos de medición como el vernier, o el tornillo micrométrico.
OBJETIVO
-
Emplear correctamente la cifra significativa para registrar los resultados de las mediciones.
-
Reconocer que todas las cantidades medidas tienen cierto grado de incertidumbre.
MARCO TEÓRICO
Concepto de cifra significativa Supongamos que se mide una distancia con una regla corriente y obtengo una medida de ![]()
, con una incertidumbre de ![]()
. Imaginemos que se necesita la raíz cuadrada del dato
Para ello usamos una calculadora y obtengo Ahora bien, éste es el resultado de la raíz cuadrada de un número natural (20). Sin embargo el valor de la medida está afectado por una incertidumbre. Si utilizamos la ley de propagación de incertidumbres
![]()
De forma que 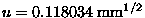
. La expresión de la incertidumbre no necesita ser tan completa. El concepto de incertidumbre y su relación con la medida implica necesariamente que la incertidumbre debe conocerse de forma estimativa. En nuestro caso es suficiente expresar la incertidumbre como 
puesto que el resto de las cifras no añade información. Supongamos entonces, que se escribe el resultado como: 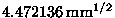
con una incertidumbre de 
. Esta expresión continúa siendo inconsistente puesto que las cifras 2136 no tienen sentido al estar afectadas por el valor de la incertidumbre. Finalmente, se llega a que la expresión correcta del resultado es: 
con una incertidumbre de 
. En esta expresión 4,4,7 son las cifras significativas del resultados, es decir, aquellas cifras de las que se está razonablemente seguro de su certeza. El resto (2,1,3,6) son cifras no significativas: no interesan. Es muy importante entender que el concepto de cifra significativa es absoluto y no depende de la coma decimal ni de las unidades que se usen en la medida. Es decir, una incertidumbre de 0.00112344 se redondea a 0.0011; y una incertidumbre de 112344 se redondea igualmente a 110000. De este último número lo único significativo son los dos unos, el resto de los ceros sólo es necesario para expresar correctamente la centena y decena de millar. A este respecto es mejor escribir el número en notación científica: 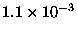
en el primer caso, y 
en el último. También se puede hacer repercutir el exponente 10 en la unidad de medida. Así se puede cambiar 
por mili, 
por kilo, etc.
MATERIALES
-
1 regla graduada en dm
-
1 regla graduada en cm
-
1 regla graduada en mm
-
Tablita con rectángulo dibujado
ANÁLISIS Y RESULTADOS
1. ¿Cuanto mide la longitud del rectángulo con la regla graduada en decímetros?
a. ¿De que medida esta en la medida que obtuvo? ¿Por que?
b. ¿De que numero no puede estar totalmente seguro? ¿Por que?
2. ¿Cuanto mide la longitud del rectángulo con la regla medida en centímetro?
a. ¿De que medida esta en la medida que obtuvo? ¿Por que?
b. ¿De que numero no puede estar totalmente seguro? ¿Por que?
3. Repita la misma medición con la regla graduada en mm ¿De que numero esta bien seguro? ¿Por que?
4. Exprese en metros la medida que obtuvo en los tres (3) casos.
a. ¿son iguales los resultados entres si? ¿Varían? ¿Cómo explicar eso?
b. ¿Depende el numero de decimales de una medida, del instrumento utilizado? ¿Como?
5.a) ¿Que instrumento le permitió tomar las medida mas Precisa? ¿Por qué considera que es mas precisa?
b) ¿El hecho de que una media sea mas precisa que la otra, esta expresado en alguna manera en las respuesta? ¿Como?
6. ¿Cuántas cifras significativas tiene?
a) La primera medida que tomo
b) La segunda
c) La tercera
d) ¿Cómo se determino el numero de cifras significativa?
7. Dentro del rectángulo dibuje un segmento.
a) Mida su longitud con las (3) reglas y exprese su respuesta en cm.
b) ¿Puede tener razonablemente un decimal su respuesta? ¿Por qué?
c) ¿Qué diferencia hay en estas dos medidas: 24cm y 24.0cm?
8. Mida la longitud del rectángulo, con la regla graduada en dm y el ancho del mismo con la regla graduada en mm.
a) Exprese sus medidas en metros
b) Con esas dos medidas ¿Cuál es el semiperimetro?
9. Evaluamos la valides de su última respuesta:
a) Las suma de una cifra cierta con otra cierta ¿da un resultado cierto o incierto?
b) La suma de una cifra incierta con otra incierta ¿Da un resultado cierto o incierto?
c) La suma de algo cierto con algo incierto ¿Da un resultado cierto o incierto?
d) Aplique estas observaciones a su suma y deduzca el número de decimales que deberá llevar el semiperimetro que usted obtuvo.
10. ¿Cuál es el área del rectángulo? (Utilice los mismos datos obtenidos en 8)
11. Evalué su respuesta para ver cuantos decimales deberá tener. Use un método similar al que utilizamos para la suma.
12. Usted mide el diámetro de un alambre delgado envolviéndolo en un lápiz, como lo hizo en el experimento 1.1 y utiliza para ello una regla graduada en mm. Su respuesta debe darle en mm.
a) ¿Cuántas cifras significas tendrá usando de 10 a 100 espiras?
b) ¿Cuántas cifras significativas tendrá, usando de 100 a 1000?
c) Evalué en que caso es mejor la medida ¿Por qué?
Con 25 espiras la medida fue de 23mm. Al hacer la operación 23/25 = 0.92mm el diámetro del alambre
a)
b)
c)
RESULTADOS
1.
a) No estamos seguro de ningún de las dos medidas por que los lados del rectángulo tanto el ancho como el largo median uno menos que el decímetro y otro mas que le decímetro como el decímetro va de diez centímetros en diez y entre estos no hay separaciones en mm y en cm, entonces no podemos dar un medida exacta.
b) No podemos estar seguro de las dos medidas por lo explicado anteriormente
2.
No estamos seguro de ninguna de las dos medidas por que los lados del rectángulo, tanto el ancho como el largo no expresan una medida exacta en centímetro si no que queda en medio de dos centímetros y por lo tanto no se puede dar una medida exacta en centímetro.
3 no estamos seguros de los dos números por las razones explicadas anteriormente
Estamos seguro de las dos medidas de los lados de rectángulo porque ya estos expresa mayor exactitud en milímetros y no queda espacios entre ellos .
4.
1m 100cm 1m 100cm
x 9 cm. x 4.9cm
x=0.109m x=0.049m
1m 10dm 1m 10dm
x 1.09dm x 0.49dm
x=0.109m x=0.049m
1m 1000mm 1m 1000mm
x 1.09dm x 49mm
x =0.109m x=0.049m
a) Los resultados entre si son iguales si son iguales o sea no varían porque las medidas son las mismas, como están expresadas en diferentes unidades de medidas y al pasarla a la unidad patrón nos da el mismo resultado.
Si depende el número decimales de una medida de acuerdo con la medida utilizada porque si toda las unidades como el centímetro, decímetro. milímetro no nos daría en metro el mismo resultado.
5.
a ) El instrumento que nos permitió tomar la medida mas precisa fue la regla graduada en milímetro por escala utilizada de 1/1000 ya que esta de mayor precisión de 1/100 y1/100 que son las escalas del decímetro y centímetro .
b) EL hecho de que una medidas sea mas precisa que la otra es que se dan por las escalas que dios anteriormente. Por mas pequeñas que sea la escala de mayor exactitud.
6.
a) La primera medida que tomamos tiene cuatros cifras significativa.
b) La segunda medida que tomamos tiene cuatro cifras significativas
c) La tercera medida que tomamos no tiene cifra significativa.
d) El número significativa se determina por el punto decimal y la cantidad de cero que tenga una fracción
7.
a) dm= 1.19
mm = 119
cm = 11,9
1cm 10mm
X 119m
X=11,9cm
1dm 10cm
1.19dm X
X = 11.9cm
b) Si se puede tener por que no dan con exactitud las medidas del segmento que trazamos en el segmento que trazamos en el rectángulo.
c) No hay ninguna diferencia ya que el cero no se puede contar como cifra significativa debido ha las reglas de manejo de cifras
8.
a) Longitud de rectángulo con la regla graduada en dm es aproximadamente 1dm y su ancho es de 49mm
1m 10dm
X 1.0dm
X=0.10m
1m 1000mm
X 49mm
X=0.049m
El semiperimetro del rectángulo es 0.10m+0.10m+0.049m+0.049m = 0.298m
9.
a) La suma de una cifra significativa cierta con otra cierta nos da un resultado cierto
b) La suma de una cifra incierta con una incierta nos da un resultado incierto
c) La suma de algo incierto con algo cierto nos da un resultado cierto por que al sumar algo cierto con algo incierto siempre nos va dar un valor cierto, pero si nos da una respuesta especifica y el resultado nos se da entonces ahí es incierto el resultado
11. a = b*h
a = 0.10m * 0.049m = 0.0049m
CONCLUSIONES
-
En algunos casos los datos podrán ser precisos pero con un grado de incertidumbre dependiendo del aparato de medida que utilizamos
-
Existe un relación de medida entre dm, cm, mm, por que estos nos permiten tener referencia al hacer una lectura de un objeto
-
Las escalas establecidas para estas unidades los mm son mas precisos comparados con los cm y estos comparado los con los dm
BIBLIOGRAFÍA
-
RAYMOND. A. Serway. Física I. 1998. Cuarta Edición. Mc GRAW - HILL México
Descargar
| Enviado por: | Loganmet |
| Idioma: | castellano |
| País: | Colombia |
