Industria y Materiales
Probabilidad
Fiabilidad
1. INTRODUCCIÓN
Definiciones
Coste asociado
2. Probabillidad como medida de fiabilidad
Aproximación Fisica
Componentes mecánicos
Modelo analítico
Bibliografía
“Mechanical Reliability”, Carter, Ed. McMillan
“Practical Reliability Engineering”, O'Connor, Ed. Jhon Wiley and Sons.
Introducción
| Fiabilidad | ! | buen funcionamiento |
| ! | coste elevado |
Definiciones fiabilidad
| Organización Europea Control de Calidad | ! | Probabilidad Tiempo Entorno especificado Prestaciones |
| Ejercito USA | ! | Probabilidad Tiempo Condiciones de mantenimiento Condiciones de uso Prestaciones |
| Institución Británica de Normalización | ! | Condiciones de uso Tiempo Prestaciones |
| Ministerio Defensa U.K. | ! | Probabilidad Tiempo Condiciones de uso Prestaciones |
| Magnitudes comunes a las definiciones | ! | Prestaciones Condiciones de uso Tiempo Probabilidad |
| R(t) | ! | Probabilidad de supervivencia, fiabilidad |
| F(t) | ! | Probabilidad de fallo |
Luego
F(t) = 1- R(t)
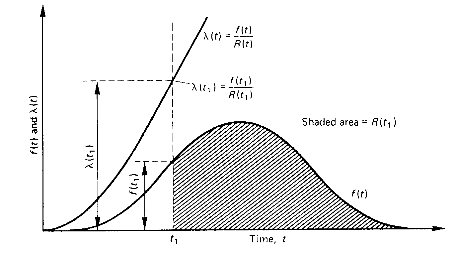
Relación de fallos
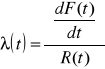
como
![]()
entonces
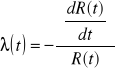
La función de densidad de probabilidad de fallo es
![]()
luego
![]()
| Fiabilidad componente | ! | No requiere mantenimiento |
| Fiabilidad equipo | ! | Conjunto de componentes ensamblados |
Coste asociado a la fiabilidad
| ! Fiabilidad | ! | ! Coste adquisición |
| ! Coste mantenimiento | ||
| ! Perdidas beneficios en producción |
Probabilidad como medida de fiabilidad
| Fiabilidad R | ! | Probabilidad de que un componente o equipo pueda realizar su trabajo bajo condiciones dadas y durante un periodo de tiempo especificado |
| 0 " R " 1 | ! | R = 0 | ! | certeza de fallo |
| R = 1 | ! | certeza de no fallo |
Probabilidad de Fallo (F) ! R + F = 1
Sistema de componentes con Ri independientes
| El fallo de un componente ocasiona el fallo del sistema | ! | Serie |
| El fallos del sistema se debe al fallo de todos los componentes | ! | Paralelo |
Fiabilidad del sistema en serie
R = R1 R2 ... Rn
Probabilidad de fallo del sistema en paralelo
F = F1 F2 ... Fn ! 1-R = (1-R1) (1-R2) ...(1-Rn)
| Sistema serie | ||
| n = 400 | ! | R = 0,8 |
| Ri = 0,9995 |
Componentes mecánicos
| Comportamiento mecánico material | ! | Resistencia | ! | Fiabilidad |
| Discontinuidades geométricas | ||||
| Proceso de fabricación | ||||
| Carga |
Características resistentes material
Carga aplicada
Modelo analítico
|
| ! | Resistencia nominal media |
| S(s) | ! | Densidad de probabilidad de resistencia |
|
| ! | Desviación standard resistencia |
|
| ! | Carga nominal media |
| L(s) | ! | Densidad de probabilidad de carga |
|
| ! | Desviación standard carga |
***Figura 3.7***
|
| ! | Coeficiente de seguridad |
En la figura
| X = 2 | ! | Coeficiente de seguridad insuficiente |
| R < 1 |
Nuevos parámetros
|
| ! | Margen de seguridad |
|
| ! | Dispersión de la carga |
Situaciones límite para sistemas en serie
| L(s) = | ! | DC = 0 | ! |
|
| S(s) | ||||
| Ri= |
| L(s) | ! | DC = 1 | ! |
|
| S(s) = | ||||
| Ri= |
| DC = 0,3 | ! | R(1) |
| DC = 0,9 | ! | R(2) |
| DC = 0,7 | ! | R(3) |
Situaciones límite para sistemas en paralelo
| L(s) = | ! | DC = 0 | ! |
|
| S(s) | ||||
| Ri= |
| L(s) | ! | DC = 1 | ! |
|
| S(s) = | ||||
| Ri= |
Fiabilidad
1
Descargar
| Enviado por: | Usuario Invitado |
| Idioma: | castellano |
| País: | España |


