Física
Principio de Arquímedes
OBJETIVO.-
-
Estudiar el principio de os cuerpos en flotación (principio de Arquímedes).
-
Determinar la densidades de algunos sólidos por los métodos: a) Directo, b) por la balanza de Jolly.
-
Comparar los valores obtenidos en ambos casos.
INTRODUCCION.-
El mundo que nos rodea esta formado por diversas sustancias tanto liquidas como sólidos, el estudio de las propiedades de estas sustancias es bastante amplio, una de las propiedades que nos interesa es a densidad, la cual estudiaremos y determinaremos mediante los métodos mencionados anteriormente.
FUNDAMENTO TEORICO.-
La densidad esta relacionado con dos parámetros muy importantes la masa y el volumen de una sustancia. A menudo podemos adivinar si una pieza esta hecha de plástico u otro material tomando solamente al objeto y apreciando su peso, por definición la densidad es la relación de la masa entre su volumen y tiene unidades (g/cm3) también se puede expresar en otras unidades como (Kg/m3), por tanto:
(1)
Para el error de la densidad se puede propagar la ecuación (1) obteniendo:
(2)
La ecuación (1) es valida siempre y cuando se tenga masa y volumen puntuales es decir que no varien con la temperatura ni que este sometido a diversos proceso externos.
Experimentalmente se puede obtener la densidad, analizando el principio de los cuerpos en flotación que dice “Cualquier cuerpo sumergido parcial o completamente en un fluido es empujado hacia arriba por una fuerza igual al fluido desplazado por el cuerpo”. Este enunciado fue planteado por Arquímedes, así la fuerza de flotación W sobre el cubo es igual al peso del fluido dentro del cubo.
(3)
donde:
E = empuje del fluido
* = densidad del fluido
g = aceleración de la gravedad (9.81 m/s2)
Una forma de demostrar este principio es por la balanza de Jolly que consiste en un resorte con una masa colgado en su extremo, es claro que el resorte debe estar el posición vertical. Inicialmente el resorte esta en equilibrio luego se agrega una masa m y se puede medir la elongación X con respecto a su posición (cero), después con la misma masa m se le puede sumergir en un fluido cualquiera. Notamos de inmediato que la elongación del resorte es menor que cuando no estaba sumergido, esto se debe precisamente al principio de Arquímedes que se denomina Empuje.
Como el sistema estará en equilibrio por la segunda ley de Newton se tiene:
(4)
(5)
En el caso a) cuando el cuerpo esta sumergido en el fluido se tiene:
(6)
(7)
Como el peso del fluido es la misma en ambos casos se puede igualar las ecuaciones (5) y (7) luego:
(8)
donde se debe tomar:
La ecuación (8) se puede escribir como:
(9)
(10)
La relación del peso del cuerpo entre el empuje esta dado por:
(11)
De la ecuación (11) se puede despejar la densidad del fluido en función a las elongaciones del resorte:
(12)
Propagando la ecuación (12) se obtiene el error de la densidad del fluido:
(13)
Realizando el mismo procedimiento para el sistema de la figura b) se obtiene la relación:
(14)
el error de la densidad:
(15)
PROCEDIMIENTO.-
PARTE I
1.- Medir las dimensiones geométricas de cuatro cuerpos distintos por lo menos tres veces.
2.- Pesar en la balanza cada uno de los cuerpos, también tres veces.
3.- Con los datos obtenidos en el inciso (1), calcular el volumen aproximado de los cuerpos.
PARTE II
1.- Colgar verticalmente el resorte, teniendo en cuenta que el resorte no debe ser defectuoso (torcido).
2.- Para distintas masas mi medir las elongaciones del resorte xi correspondientes. Dichas mediciones se debe realizar sin introducir en ningún fluido.
3.- Para las mismas masas mi medir las elongaciones xi, pero introduciendo el sistema en un fluido (agua). Anotar las observaciones pertinentes.
PARTE III
1.- Pesar el sistema Vaso -agua en la balanza y registrar su masa mv + mag, Fig. %%.
2.- Introducir un cuerpo de masa mi en el sistema descrito anteriormente, dicho cuerpo debe estar suspendido por un hilo, registrar el nuevo peso mv + mag + mc.
3.- Realizar el inciso (2) para distintas masas mi registrando las masas correspondientes.
PARTE IV
1.- En el resorte de la Fig. && colgar distintas masas mi y medir las elongaciones correspondientes, pero esta ves se realizara sumergido en aceite comestible.
2.- Repetir el inciso anterior pero usando esta ves aceite de motor de densidad conocida. Y registrar los datos necesarios para la elaboración de cálculos.
DATOS EXPERIMENTALES.-
PARTE I Mediciones de cuerpos geométricos
| Tabla # 1 | Tabla # 2 | |||||||||
| n | m1 (g) | D (mm) | n | D (mm) | ||||||
| 1 | 9,9 | 7,04 | 14,85 | 1 | 36,3 | 15 | 19,3 | |||
| 2 | 9,9 | 7,1 | 14,81 | 2 | 36,3 | 15,2 | 19,4 | |||
| 3 | 9,8 | 7,04 | 14,82 | 3 | 36,2 | 15,2 | 19,2 | |||
| Tabla # 3 |
| Tabla # 4 | ||||||||
| n | m3 (g) | (mm) | D (mm) | dint (mm) | n | m4 (g) | D (mm) | |||
| 1 | 49,8 | 13,42 | 25,38 | 7,58 | 1 | 52,3 | 17,22 | 19,3 | 30.54 | |
| 2 | 49,9 | 13,44 | 25,4 | 7,54 | 2 | 52,4 | 17,2 | 19,3 | 30.60 | |
| 3 | 49,8 | 13,45 | 25,42 | 7,52 | 3 | 52,4 | 17,26 | 19,4 | 30.62 | |
| PARTE II Tabla # 5 | Sin fluido | Tabla # 6 | En fluido | |||||||
| n | mi (g) | Xi (cm) | n | Xi (cm) | ||||||
| 1 | m1 | 0,3 | 1 | 1 | 0,2 | |||||
| 2 | m2 | 3,0 | 2 | 2 | 2,5 | |||||
| 3 | m3 | 4,3 | 3 | 3 | 3,7 | |||||
| 4 | m4 | 4,5 | 4 | 4 | 3,9 | |||||
| PARTE III Tabla # 7 | ||||||||||
| n | m1+mT (g) | m1+mT (g) | m1+mT (g) | m1+mT (g) | ||||||
| 1 | 578,1 | 581 | 582,5 | 582,4 | ||||||
| 2 | 578,2 | 581,1 | 582,3 | 582,3 | ||||||
| PARTE IV Tabla # 8 | Tabla # 9 | |||||||||
| n | mi (g) | Xi (cm) | n | mi (g) | Xi (cm) | |||||
| 1 | 2,8 | 1 | 2,6 | |||||||
| 2 | 3,8 | 2 | 3,8 | |||||||
CALCULO DE DATOS.-
Para calcular la densidad de los cuerpos geométricos, primero se debe calcular los volúmenes y las masas de los objetos (m1, m2, m3, m4), según las formulas requeridas.
Para m1:
(*)
De la tabla # 1 se tienen los valores de diámetro y altura, luego reemplazando:
Propagando la ecuación (*) para el error de volumen:
(**)
Como se puede ver esta en función de , de modo que para todos los casos debemos calcular .
Luego remplazando en (**)
Para el error de la masa:
Utilizando las ecuaciones ()() se obtiene:
Para la masa m2:
Calculando el error del volumen:
La densidad será:
Para m3:
Como se trata de un cilindro hueco se tiene para el volumen:
propagando:
Para m4:
Y h2 = htotal -h1
PARTE II
Las ecuaciones ()() representan el valor promedio y el error de la densidad del fluido, que esta en función de los errores del cuerpo y de las elongaciones del resorte. Con los valores calculados en la PARTE I se puede calcular la densidad del fluido y su correspondiente error:
Para m1:
Para m2:
Para m3:
Para m4:
PARTE III
De la ecuación () y ademas de los valores calculados anteriormente se puede calcular la densidad del cuerpo cuando esta sumergido.
mg
Fr
mg
Mediciones de cuerpos en flotación
Elongaciones de resorte para distintas masas
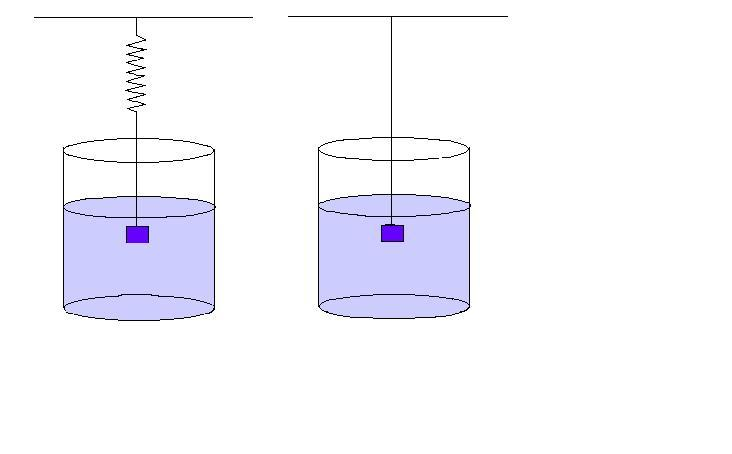
T
E
E
a)
b)
Fig. 1
Fig. 2
Descargar
| Enviado por: | Bburgoa |
| Idioma: | castellano |
| País: | Bolivia |
