Matemáticas
Parábola
INTRODUCCION
Las parábolas aparecen en diferentes situaciones de la vida cotidiana. Se puede apreciar claramente cuando lanzamos un balón bombeado o golpeamos una pelota de tenis. En la curva que describe la pelota en su movimiento se puede ver que se trata de una trayectoria parabólica. Al dibujar este desplazamiento, podemos considerar esta parábola como la representación gráfica de una función que asigna a cada desplazamiento horizontal `x' la altura `y' alcanzada por la pelota.
Una vez situada la parábola en este marco, que es un sistema de coordenadas cartesianas, son visibles dos propiedades fundamentales: tiene un punto extremo, que corresponde al instante en el que la pelota alcanza la altura máxima. Este punto es el vértice de la parábola; y la segunda, en la que las alturas a las que llega la pelota son las mismas en posiciones horizontales equidistantes de la abcisa del vértice. Por tanto, la recta paralela al eje de ordenadas que pasa por el vértice es el eje de simetría de la parábola.
En terminos generales, se podría definir la parábola como la sección cónica -al igual que la elipse y la hipérbola- que se obtiene al cortar la superficie cónica con un plano paralelo a una generatriz. Es una curva que se construye por la relación que existe entre sus puntos, un punto fijo llamado foco -'F'- y una recta llamada directriz -'d'-. La recta que pasa por `F' y es perpendicular a la directriz es el eje de la parábola y su eje de simetría. El punto de corte de la parábola con su eje es el vértice.
La parábola es una de las curvas cónicas más utilizadas en la tecnología actual. Un ejemplo son las antenas parabólicas que sirven para captar las señales de televisión emitidas por un satélite. Con ella podemos ver emisoras de televisión de todas partes del mundo. Del mismo modo, la parábola también se emplea para fabricar los faros de los coches.
PARÁBOLAS
Name=1; HotwordStyle=BookDefault; Se llama parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija llamada directriz.
La distancia entre el foco y la directriz de una parábola recibe el nombre de parámetro de la parábola (suele denotarse por p).
Dada una parábola, se llama eje de la misma la recta que contiene al foco y es perpendicular a la directriz.
Se llama vértice de la parábola al punto donde ésta corta a su eje.
Para simplificar la parábola, se supondrá que el vértice es el origen de coordenadas y que el foco se encuentra en el semieje positivo de abscisas.
Ecuación canónica de la parábola
La ecuación de la parábola con vértice en el origen de coordenadas y foco en el ![]()
y = 2px
Demostración:
Name=2; HotwordStyle=BookDefault;
![]()

![]()
La condición para que el punto esté en la parábola es que ambas coincidan:
Name=3; HotwordStyle=BookDefault;
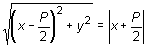
Elevando al cuadrado:
![]()
![]()
-px + y2 = px ð y2 = 2px
Hay otros tres casos elementales de parábolas:
Name=3; HotwordStyle=BookDefault;
ð Si el eje es horizontal y el foco está en el semieje negativo de abscisas, la ecuación es y2 = -2px.
ð Si el eje es vertical y el foco está en el semieje positivo de ordenadas, la ecuación es x2 = 2py.
ð Si el eje es vertical y el foco está en el semieje negativo de ordenadas, la ecuación es x2 = -2py.
Parábola con vértice en un punto cualquiera
Si el vértice de una parábola se encuentra en un punto (x0, y0) su ecuación será, según los casos:
Name=4; HotwordStyle=BookDefault;
ð Eje horizontal y foco a la derecha: (y-y0)2 = 2p(x-x0)
ð Eje horizontal y foco a la izquierda: (y-y0)2 = -2p(x-x0)
ð Eje vertical y foco por encima: (x-x0)2 = 2p(y-y0)
ð Eje vertical y foco por debajo: (x-x0)2 = -2p(y-y0)
Reducción de la ecuación de una parábola
Dada una ecuación del tipo Ax2 + Bx + Cy + D = 0 o del tipo Ay2 + Bx + Cy + D = 0, siempre es posible reducirla a la ecuación de una parábola. Para ello se completa un cuadrado y se manipula adecuadamente el otro miembro.
Ejercicio: ecuaciones de parábolas
ð Hallar la ecuación reducida de la parábola 2x2 + 8x + 3y - 5 = 0. Hallar su vértice, su foco y su directriz.
ð Se ha de transformar esta ecuación en una de la forma:
Name=5; HotwordStyle=BookDefault;
(y - y0)2 = ± 2p(x - x0) ó (x - x0)2 = ± 2p(y - y0)
ð La ecuación dada tiene un término en x2. Habrá que transformarla, pues, en una del tipo (x - x0)2 = ± 2p(y - y0)
ð 2x2 + 8x + 3y - 5 = 0 ð 2x2 + 8x = -3y + 5 ð
![]()
x2 + 3x = (x + 2)2 - 4. Se sustituye en la ecuación:
![]()
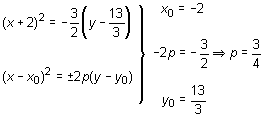
ð Se trata de una parábola con el eje vertical y el foco por debajo del vértice.
![]()
ð Para hallar el foco se le resta la mitad del parámetro a la ordenada del vértice:
![]()
ð Por ser el eje vertical, la directriz es horizontal, y su ordenada se obtiene sumándole la mitad del parámetro a la del vértice:
![]()
ð Hallar los elementos de la parábola y2 - 4x + 6y + 13 = 0.
Resolución:
Name=6; HotwordStyle=BookDefault;
ð Se opera como en el caso anterior, teniendo en cuenta que ahora la variable que aparece elevada al cuadrado es y:
y2 + 6y = 4x - 13
y2 + 6y = y2 + 2 · 3y + 32 - 32 = (y+3)2 - 9.
(y+3)2 - 9 = 4x - 13 ð (y+3)2 = 4x - 4
(y+3)2 = 4(x-1)
ð Es una parábola con vértice en el punto (1, -3).
![]()
vértice.
![]()
ð La directriz se obtiene restándole la mitad del parámetro a la abscisa del vértice: x = 1 - 1 = 0. La directriz es el eje de ordenadas.
Intersecciones de una cónica con una recta
Name=7; HotwordStyle=BookDefault; Para calcular la intersección de una cónica con una recta se ha de resolver un sistema de ecuaciones, que dará lugar a una ecuación de segundo grado (ax2 + bx + c = 0). Al resolver esta ecuación, se obtienen resultados distintos dependiendo del valor que tome el discriminante (ð = b2 - 4ac):
ð Si el discriminante es negativo (b2 - 4ac < 0, la ecuación no tiene soluciones reales; sus dos soluciones son números complejos conjugados), el sistema no tiene solución. La recta no corta a la cónica y se dice que es exterior a ella.
ð Si el discriminante es nulo (b2 - 4ac = 0, la ecuación tiene dos soluciones reales iguales), la recta corta a la cónica en un solo punto. En este caso se dice que la recta es tangente a la cónica.
ð Si el discriminante es positivo (b2 - 4ac > 0, la ecuación tiene dos soluciones reales y distintas), la recta tiene dos puntos comunes con la cónica. Entonces se dice que la recta es secante a la cónica.
Ejercicio: intersección de cónicas y rectas
ð Hallar los puntos de intersección de la recta x + y + 1 = 0 y la elipse
2x2 + 3y2 - 4x + 6y - 9 = 0.
Resolución:
Name=8; HotwordStyle=BookDefault;
![]()
x = -y - 1
2(-y - 1)2 + 3y2 - 4(-y - 1) + 6y - 9 = 0
5y2 + 14y - 3 = 0

![]()
ð Trazar una tangente vertical a la cónica x2 - y2 + 2x + y - 2 = 0.
Resolución:
ð Las rectas verticales son de la forma x = k
ð Sustituyendo este valor en la ecuación:
k2 - y2 + 2k + y - 2 = 0,
-y2 + y + (k2 + 2k - 2) = 0
ð Su discriminante es
b2 - 4ac = 1 - 4 (-1) (k2 + 2k - 2) = 1 + 4k2 + 8k - 8 = 4k2 + 8k - 7
La condición para que la recta sea tangente es que dicho discriminante sea nulo:
![]()
Name=9; HotwordStyle=BookDefault;
4k2 + 8k - 7 = 0
![]()
Las tangentes verticales son:
![]()
ð Hallar las rectas tangentes a la curva y2 = 4x que contengan al punto (-1, 0).
Resolución:
Name=10; HotwordStyle=BookDefault;
ð Cualquier recta que contenga a dicho punto tiene una ecuación de la forma y = m(x + 1), donde m es la pendiente.
ð Sustituyendo en la ecuación de la parábola:
m2(x + 1)2 = 4x ð m2x2 + 2m2x + m2 = 4x ð
ð m2x2 + (2m2 - 4)x + m2 = 0
ð El discriminante es
(2m2 - 4)2 - 4m2 · m2 =
= 4m4 - 16m2 + 16 - 4m4 = -16m2 + 16
ð La recta será tangente si este discriminante es nulo:
-16m2 + 16 = 0 ð 16m2 = 16 ð
ð m = ±1
ð Las tangentes buscadas son:
y = x + 1 e y = -(x + 1)
La parábola es la gráfica de la función cuadrática o polinomio de segundo grado, cuya ecuación general es y=ax2+bx+c, donde a, b y c son números reales.
Se trata de una curva muy interesante y muy común. Aparece en numerosos fenómenos naturales o, cuando menos frecuentes, en nuestras ciudades: el caño de una fuente, la trayectoria que describe un balón de fútbol en un golpe franco, el movimiento de un proyectil disparado por un cañón,...
La definición geométrica de la parábola es algo más complicada:
-
La parábola es el conjunto de los puntos del plano que se encuentran a la misma distancia de un punto fijo F (que se llama foco) y de una recta también fija d (que se llama directriz).

En la siguiente gráfica puedes comprobar la definición:
No deja de ser curioso que una curva tan común y tan frecuente responda a una definición matemática, aparentemente, tan artificial como la anterior. No obstante no se acaban ahí las curiosidades matemáticas de esta gráfica. La parábola esta incluida, junto a otras curvas, dentro de un grupo que recibe el nombre de cónicas. Reciben este nombre porque se obtienen cortando un cono, mediante un plano, de una determinada manera.
En concreto, la parábola se obtiene, cortando un cono con un plano paralelo a una de las directrices del mismo.

LA PARÁBOLA DE ECUACIÓN Y=AX2
Decimos que la ecuación de esta parábola es incompleta, esto se debe a que no aparecen los términos bx y c, es decir b=c=0.
ÁREA DE UN SEGMENTO PARABÓLICO
Cuando Arquímedes escribió su tratado "La cuadratura de la parábola", las secciones cónicas eran bien conocidas desde hacía casi un siglo, pero aún no se había hecho progreso alguno en el cálculo de áreas relacionadas con ellas. La doble vía en la que Arquímedes aborda el problema y que aquí se expone, ilustra la manera de pensar del gran sabio griego.
El primer camino, contenido en el libro El método, muestra cómo empleó ideas provenientes de la mecánica para obtener resultados correctos.
Arquímedes considera el segmento de parábola formado por el arco ABC y el segmento AC ( ver dibujo). Traza la recta CE que es tangente a la parábola en el punto C. Sea D el punto medio del segmento AC. Hace pasar por D una recta paralela al eje de la parábola que corta en B a la curva y en E a la tangente. Afirma que BD es igual a EB y por proporcionalidad en cualquier segmento paralelo a ED se cumple que MN es igual a NO. Traza la recta CB que prolonga hasta H con la condición de que KH es igual que CK.
La brillante idea de Arquímedes es la siguiente: Se da cuenta (lo demuestra) que HK·OP es igual que MO·KN, lo que significa, según la ley de la palanca, que si consideramos el segmento HN como una palanca con el punto K como fulcro y con H y N como platillos, el segmento MO apoyado en N equilibra al segmento OP apoyado en H. De manera genial (anticipándose en casi veinte siglos a Cavalieri), considera que los segmentos de la forma MO llenan el triángulo ACF y los segmentos de la forma PO llenan el segmento parabólico. Por lo tanto el área del triángulo ACF equilibrará al área del segmento parabólico.
La cuestión ahora es que el "platillo" H permanece fijo, mientras que el "platillo" N se desplaza según el tamaño del segmento MO. Para resolver esta cuestión Arquímedes recurre a un resultado de su libro Sobre el equilibrio de los planos en el que prueba que el centro de gravedad del triángulo es el punto X de tal manera que KX = (1/3)CK. De esta manera el área del triángulo apoyado en el platillo X es igual al área del segmento parabólico apoyado en el platillo H por lo tanto por la ley de la palanca:
KX·( área del triángulo ACF) = HK·( área del segmento parabólico)
Como CK el igual a HK y KX = (1/3)CK tenemos que
(1/3)HK·( área del triángulo ACF) = HK·( área del segmento parabólico)
Por lo tanto el área del triángulo ACF es tres veces el área del segmento parabólico.
Arquímedes relaciona ahora el área del triángulo ACF con la del triángulo ABC de la manera siguiente: Es fácil comprobar por proporcionalidad que la altura del triángulo ABC es la mitad de la altura del triángulo ACK. Como la base de los triángulos es la misma (AC) resulta que el área del triángulo ABC es la mitad del triángulo ACK y a su vez el triangulo ACK es la mitad del triángulo ACF. Entoces el área del triángulo ABC es la cuarta parte del área del triángulo AFK y por lo tanto el área del segmento de parábola ABC es al área del triángulo ABC como 4 es a 3. Es decir en notación moderna
área del segmento de parábola = (4/3) área del triángulo ABC
con lo cual Arquímedes consigue cuadrar (es decir, trasformar el área bajo una curva en el área de una figura rectilínea ) el segmento parabólico.
Arquímedes consideraba esta manera de razonar como un método de descubrimiento, puesto que el argumento de llenar las figuras mediante líneas no le parecía formalmente correcto. Por eso, en su libro "Sobre la cuadratura de la parábola" da una demostración rigurosa. Él sabe ya el resultado que quiere probar y se dispone a hacerlo con todo rigor geométrico.
Para ello considera el segmento parabólico ABC en donde el punto B es obtenido al cortar la parábola por una recta paralela al eje que pasa por O, el punto medio de AC. Inscribe en segmento el triángulo ABC. Traza entonces la tangente a la parábola en B. Es intuitivamente claro que la tangente es paralela al segmento AC lo que es probado por Arquímedes es su proposición 18
A continuación se trazan dos rectas paralelas a OB por A y por G que cortan a la recta tangente en B en los puntos M y N respectivamente. Como el triángulo ABC es la mitad del paralelogramo ACNM, resulta que el triángulo ABC es mayor que la mitad del segmento parabólico.
Arquímedes construye ahora otros dos triángulos ABD y BCE de la misma forma que en el párrafo anterior. Los nuevos triángulos ADB y BCE son mayores que la mitad de los segmentos parabólicos ADB y BEC respectivamente. Como esta construcción se puede repetir indefinidamente será posible aproximarse al segmento parabólico tanto como se quiera.
Arquímedes sabe que el área del triángulo ABD es la cuarta parte del área del triángulo AMB que es igual al triángulo AOB. De la misma manera, el área del triángulo BCE es la cuarta parte del triángulo OCB por tanto
área triángulo ADB + área triángulo BCE = (1/4) área triángulo AOB + (1/4) área triángulo OBC = = (1/4) área triángulo ABC
Así pues, podemos afirmar que el área de la figura poligonal obtenida al añadir triángulos al triángulo original ABC, es decir el área de
Triángulo ABC + (1/4) triángulo ABC + (1/16) triángulo ABC + ........(1)
con una cantidad finita de términos se aproxima al segmento parabólico tanto como se quiera. (Proposición 1del libro X de los elementos de Euclides)
Arquímedes se encuentra ahora con la difícil cuestión de sumar la serie anterior (o mejor dicho, en demostrar que dicha serie suma 4/3 del triángulo ABC, puesto que, como hemos visto ya, el resultado le era conocido por medio de su método mecánico) . En la actualidad, un estudiante aplicado de bachillerato sabe sumar la serie geométrica infinita 1 + 1/4 + 1/16 + 1/64 ......... Pero el gran Sabio no disponía ni de nuestro sistema de numeración, ni de nuestro lenguaje del álgebra simbólica por lo que estas dificultades las suplía derrochando mucha imaginación y enorme talento. Veamos como:
Arquímedes demuestra primero el siguiente curios teorema: Sea S = A + B + C + D + E, y, además A:B = B:C = C: D = D:E = 4:1 Entonces se verifica que S = (4/3) A - (1/3) E
La demostración dada por Arquímedes es farragosa, pero nosotros con ayuda de nuestra álgebra simbólica pronto nos convencemos de la veracidad del teorema. En efecto, multipliquemos la expresión inicial por 4/3
(4/3)·S = (4/3)· ( A + B + C + D + E ) = (4/3)· A + (1/3)·( 4B + 4C + 4D + 4E )
como por hipótesis 4B = A; 4C = B; 4D = C; 4E = D tenemos que
(4/3)· A + (1/3)·( 4B + 4C + 4D + 4E ) = (4/3)· A + (1/3)·( A + B + C + D)
sumando y restando ahora (1/3)· E obtenemos
(4/3)·S = (4/3)· A + (1/3)·( A + B + C + D + E ) - (1/3)·E
luego
(4/3)·S = (4/3)· A + (1/3)·S - (1/3)·E
y restando (1/3)·S a los dos miembros de la igualdad anterior obtenemos lo que queríamos demostrar.
Hay que observar que este teorema se puede extender a cualquier número de sumandos por lo que Arquímedes lo aplica a la serie (1).
An = A + A/4 + A/16 + A/64 +......+ A/(4n-1) = (4/3)·A - (1/3)·A/(4n-1) (2)
en donde A = área del triángulo ABC. Como el último término se puede hacer tan pequeño como queramos, tenemos que para un n suficientemente grande, An = (4/3)·A .
Arquímedes prueba ahora que el área del segmento parabólico no puede ser ni mayor ni menor que (4/3)·A. Para ello utiliza el método de reducción al absurdo que consiste en lo siguiente:
Llamemos S al área del segmento parabólico. Entonces puede ocurrir una de estas tres cosas: o bien S > (4/3)·A o bien S < (4/3)·A o bien S = (4/3)·A. Arquímedes prueba que si supone S > A llega a un resultado falso lo que indica que la hipótesis de partida no es cierta. Prueba lo mismo si (4/3)·A < S por lo que concluye que la tercera hipótesis S = (4/3)·A es la correcta. Veamos como lo consigue.
Supongamos S > (4/3)·A. Entonces la cantidad S - (4/3)·A sería positiva y se puede escoger un conjunto finito de triángulos cuya suma de sus áreas S' difiera del área S del segmento en una cantidad menor que cualquier magnitud dada, por lo tanto S > S' > (4/3)·A
Pero si S' contiene n términos por la expresión (2) se tiene S' + (1/3)·A/4n-1 = (4/3)A, lo que implica que S' < (4/3)·A y contradice la hipótesis de partida.
Supongamos ahora que S < (4/3)·A. Entonces la cantidad (4/3)·A - S es positiva. Como los triángulos inscritos son cada vez más pequeños existirá un triángulo de la sucesión n cuya área sea más pequeña que la cantidad (4/3)·A - S, es decir A/(4n-1) < (4/3)·A - S, en donde A/(4n-1) representa el término enésimo de la sucesión de triángulos, utilizando otra vez la expresión (2)
A + A/4 + A/16 + A/64 +......+ A/(4n-1) = (4/3)·A - (1/3)·A/(4n-1)
Reordenando términos resulta
(1/3)·A/(4n-1) = (4/3)·A -(A + A/4 + A/16 + A/64 +......+ A/(4n-1))
De lo cual podemos deducir
A/(4n-1) > (4/3)·A -( A + A/4 + A/16 + A/64 +......+ A/(4n-1))
Reordenando de nuevo
( A + A/4 + A/16 + A/64 +......+ A/(4n-1)) > (4/3)·A - A/(4n-1)
y como A/(4n-1) < (4/3)·A - S resulta que S < (4/3)·A - A/(4n-1)
por lo tanto
( A + A/4 + A/16 + A/64 +......+ A/(4n-1)) > (4/3)·A - A/(4n-1) > S
Pero esta última expresión es imposible puesto que la suma de triángulos inscritos nunca puede ser superior al área del segmento, luego S < (4/3)·A es imposible y por lo tanto S = (4/3)·A
Una vez terminada la demostración aparece la realidad. ¡Arquímedes ha sumado una serie infinita! algo que no harán los matemáticos hasta el siglo XVII, pero, ¡qué diferencia de rigor!. El cuidadoso tratamiento del infinito realizado por Arquímedes es muy superior a "esas diferencias evanescentes" que con cierta razón criticaba el obispo Berkeley en los trabajos de Newton y Leibniz, los cuales no llegaron a fundamentar de una manera convincente su nuevo cálculo diferencial.
Descargar
| Enviado por: | El ogro |
| Idioma: | castellano |
| País: | Perú |
