Electrónica, Electricidad y Sonido
Osciladores de cristal
TIPOS DE CRISTALES
-
CRISTALES DE CUARZO
Algunos cristales encontrados en la naturaleza presentan el efecto piezo-electrico. Cuando se aplica una tensión alterna a través de ellos, vibran a la frecuencia de la tensión aplicada de manera que inversa si mecánicamente se les obliga a que vibren, generan una tensión alterna de la misma frecuencia. Las principales sustancias que producen el efecto piezo-electrico son el cuarzo las sales de rochelle y la turmalina.
La piezo-electricidad es electricidad creada por una presión mecánica. En un material piezoeléctrico, al aplicar una presión mecánica sobre un eje, dará como consecuencia la creación de una carga eléctrica a lo largo de un eje ubicado en un ángulo recto respecto al de la aplicación de la presión mecánica.
En algunos materiales, se encuentra que aplicando un campo eléctrico según un eje, produce una deformación mecánica según otro eje ubicado a un ángulo recto respecto al primero.
Las sales de rochelle tienen la mayor actividad piezoeléctrica Con una tensión alterna, vibran mas que el cuarzo o la turmalina.
Mecánicamente, son los mas débiles porque se quiebran muy fácilmente.
Estas sales se han empleado para hacer micrófonos, agujas fonocaptoras audífonos y altavoces. La turmalina muestra actividad piezoeléctrica mínima, pero es la mas resistente de las tres. Es también la mas cara de las tres Ocasionalmente se usa en frecuencias muy altas. El cuarzo ocupa un lugar intermedio entre la actividad piezoeléctrica de las sales de rochelle y la dureza de la turmalina.
El cristal de cuarzo es utilizado como componente de control de la frecuencia de circuitos osciladores convirtiendo las vibraciones mecánicas en voltajes eléctricos a una frecuencia específica.
-
CORTES DEL CRISTAL
La forma natural del cristal de cuarzo es un prisma hexagonal con pirámides en sus extremos (fig. 1) . Para tener un cristal útil, debemos cortar una lamina rectangular del cristal natural.
La figura 2 muestra una lamina con un espesor t. El numero laminas que podemos obtener de un cristal natural depende de su tamaño y el ángulo de corte.
Hay diferentes formas de cortar el cristal natural, cada corte tiene propiedades piezoeléctricas distintas.
Figura 1 figura 2
La siguiente figura muestra la ubicación de elementos específicos dentro de una piedra de cuarzo
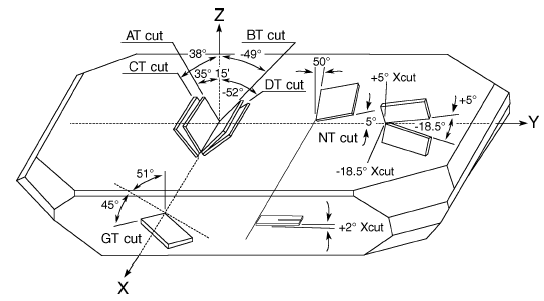
De los cortes que se pueden hacer, el corte "AT" es el más popular y es fabricado hasta frecuencias relativamente altas, mostrando una excelente estabilidad de frecuencia frente a las variaciones de la temperatura.
La siguiente gráfica muestra la variación en partes por millón (PPM) con respecto a la temperatura.

Para utilizarla en circuitos electrónicos, la lamina debe montarse entre dos placas de metal, como en la figura 3. En este circuito la vibración del cristal depende de la frecuencia de la tensión aplicada.
Al cambiar la frecuencia podemos encontrar frecuencias de resonancia a las cuales las vibraciones del cristal alcanzan un punto máximo. Puesto que la energía de las vibraciones debe ser proporcionadas por un generador de señal, la corriente es máxima en cada frecuencia resonante.
FRECUENCIA FUNDAMENTAL Y SOBRETONOS
Casi siempre el cristal se corta y se monta para vibrar adecuadamente en una de sus frecuencias de resonancia, generalmente la frecuencia fundamental o frecuencia mínima. Las frecuencias de resonancia mayores, llamadas sobretónos, son múltiplos casi exactos de la frecuencia fundamental. Por ejemplo, un cristal con una frecuencia fundamental de 1Mhz tiene un primer sobretono aproximadamente de 2 Mhz, un segundo sobretono aproximadamente de 3 Mhz, y así sucesivamente.
La formula de la frecuencia fundamental de un cristal es f = K/t
donde K es una constante que depende del corte y otros factores, y t es el espesor del cristal. Es obvio que la frecuencia fundamental es inversamente proporcional al espesor.
Por esta razón, hay un límite practico para la frecuencia mas alta que se puede alcanzar. Cuanto mas delgado sea el cristal, mas frágil es y mayor probabilidad hay de que se rompa debido a las vibraciones.
Los cristales de cuarzo trabajan adecuadamente hasta los 10 Mhz de frecuencia fundamental. Para lograr frecuencias mas altas, podemos emplear un cristal que vibre en los sobretonos. De esta forma, podemos alcanzar frecuencias de hasta 100Mhz. Ocasionalmente, la turmalina, mas cara, pero mas resistente se emplea a frecuencias mayores.
CIRCUITO EQUIVALENTE PARA SEÑAL
El capacitor CO o capacidad en paralelo, representa en total la capacidad entre los electrodos del cristal más la capacidad de la carcaza y sus terminales. R1,C1 y L1 conforman la rama principal del cristal y se conocen como componentes o parámetros motional donde:
L1 representa la masa vibrante del cristal,
C1 representa la elasticidad del cuarzo y
R1 representa las pérdidas que ocurren dentro del cristal.
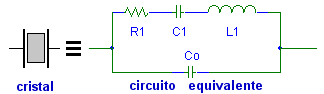
figura 4
Cuando el cristal de la figura, 4a, no esta vibrando, es equivalente a una capacitancia Co por estar compuesto de dos placas de metal separadas por un dieléctrico. Co recibe el nombre de capacitancia del encapsulado.
Cuando el cristal está vibrando, el circuito equivalente se hace mas interesante. Un cristal que vibra actúa como un circuito sintonizado. En la figura 4b, se observa el circuito equivalente se observa el circuito equivalente para señal alterna de un cristal vibra a su frecuencia fundamental o cerca de ella.
Los valores característicos son L en henrios, C1 en fracciones de pico faradio, R1 en cientos de ohmio y Co en pico faradios. Además los valores de el corte, el espesor y el montaje de la lamina influyen en esos valores.
Los cristales tienen una Q increíblemente alta. Para los valores de L=3H, C1=0.05pF, R1=2K y CO=10pF, podemos calcular una Q de mas de 3.000. La de los cristales puede fácilmente estar alrededor de 10.000. La Q extremadamente alta de un cristal genera osciladores con frecuencias muy estables. Este hecho puede corroborarse empleando la ecuación anteriormente vista:
fr=(1/2pi*"(LC))
Cuando Q tiende a infinito, como sucede en un cristal, la frecuencia de resonancia se aproxima al valor ideal determinado por L y C. Estos valores de L y C están determinados exactamente en un cristal. En cambio, el circuito tanque LC normal tiene una L y una C con grandes tolerancias, por lo que su frecuencia no se controla con precisión, como sucede con un oscilador de cristal.
La frecuencia de resonancia paralelo fP de un cristal es la frecuencia a la cual la corriente de lazo de la figura 4b alcanza su valor máximo. Puesto que esta corriente debe circular a través de la combinación en serie de C1 y de CO, Clazo equivalente es
Clazo = C OC 1/(C1+CO)
La frecuencia de resonancia en paralelo es
fR=(1/2*"(LClazo))
Dos capacidades en serie siempre producen una capacidad menor que cualquiera de las dos. En consecuencia Clazo es menor C1 y fp es mayor que fs.
En cualquier cristal, C1 es mucho menor que Co . Por ejemplo, con los valores dados anteriormente, C1 fue de 0.05pF y Co fue de 10pF. Debido a esto, la ecuación de Clazo, esta da un valor ligeramente menor que C1. Ello significa que fp es ligeramente menor que fs.
Cuando se utilice un cristal en un circuito equivalente para señal alterna como el de la figura 5, las capacidades adicionales del circuito aparecen en paralelo con Co. Por esta causa, la frecuencia de oscilación estará entre fs y fp. Esta es la ventaja de conocer los valores de fs y f p; estos fijan los limites inferior y superior de la frecuencia de oscilación.
Figura 5
POTENCIA DE TRABAJO (DRIVE LEVEL)
Es la potencia disipada por el cristal. Está normalmente especificada en micro o milivatios, siendo un valor típico 100 microvatios.
TOLERANCIA EN LA FRECUENCIA
La tolerancia en la frecuencia se refiere a la máxima desviación permitida y se expresa en partes por millón (PPM) para una temperatura especificada, usualmente 25°C.
ESTABILIDAD DE LA FRECUENCIA
La estabilidad de la frecuencia se refiere a la máxima desviación en PPM, en un determinado rango de temperatura. La desviación esta tomada con referencia a la frecuencia medida a 25°C.
ENVEJECIMIENTO
El envejecimiento se refiere a los cambios acumulativos en la frecuencia del cristal con el transcurrir del tiempo.
Los factores que intervienen son: exceso en la potencia disipada, efectos térmicos, fatiga en los alambres de armado y pérdidas en la elasticidad del cristal.
El diseño de circuitos considerando bajas temperaturas ambientales y mínimas potencias en el cristal reducirán el envejecimiento.
CURVA DE IMPEDANCIA
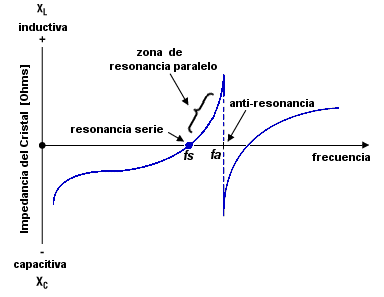
Un cristal tiene dos frecuencias de fase cero, como se ven en la siguiente figura. La más baja es la Frecuencia de Resonancia Serie indicada como fs. En éste punto el cristal se comporta como una resistencia en el circuito, la impedancia está en un mínimo y la corriente que circula es la máxima.
A medida que se incrementa la frecuencia, el cristal pasa por la Frecuencia de Resonancia Paralelo y llega a la frecuencia de Antiresonancia fa en la cual la impedancia es máxima, y las reactancias de la L1 y la Co se cancelan. En éste punto, la corriente que circula por el cristal es la mínima.
Factor de Calidad (Q)
El factor de calidad (Q) es una medida de la eficiencia de la oscilación. La máxima estabilidad obtenible de un cristal depende de el valor de "Q".
En la figura de la impedancia del cristal, la separación entre las frecuencias serie y paralelo se llama ancho de banda. Cuanto más pequeño el ancho de banda mayor es el "Q". Cambios en la reactancia del circuito externo tienen menos efecto (menos "pullability") en un cristal de alto "Q" por lo tanto la frecuencia es en definitiva más estable.
RESONANCIA SERIE Y PARALELO
Además de la Q, L1, R1 y CO de un cristal, hay otras dos características que debemos conocer. La frecuencia de resonancia de la rama RCL en la figura 4b. A esta frecuencia, la corriente de rama alcanza su valor máximo porque L1 esta en resonancia con C1.
CIRCUITOS OSCILADORES SERIE
Un circuito básico oscilador resonante serie, utiliza un cristal que está diseñado para oscilar en su frecuencia resonante serie natural. En éste circuito no hay capacitores en la realimentación Los circuitos resonantes serie son usados por la baja cantidad de componentes que se utilizan, pero estos circuitos pueden tener componentes parásitos que intervienen en la realimentación. y en el caso que el cristal deje de funcionar oscilarán a una frecuencia impredecible. El esquema del circuito oscilador serie es:
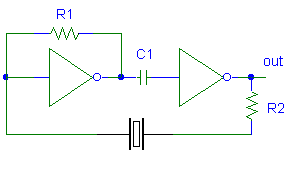
De la figura del circuito básico del oscilador resonante serie se ve que no existen componentes para ajustar la frecuencia de oscilación. R1 es utilizado para polarizar el inversor en su región lineal de operación y además provee realimentación negativa al inversor. C1 es un capacitor de acople para bloquear la componente de continua. R2 está para controlar la potencia que se entrega al cristal, limitando la corriente a través de él.
CIRCUITOS OSCILADORES PARALELO
Un circuitos oscilador paralelo utiliza un cristal que está diseñado para operar con un valor específico de capacidad de carga. Esto resultará en un cristal que tendrá una frecuencia mayor que la frecuencia resonante serie, pero menor que la verdadera frecuencia resonante paralelo.
Un circuito básico se muestra a continuación.
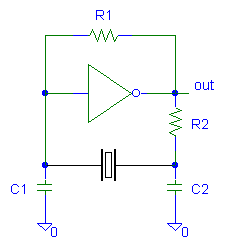
Este circuito utiliza un inversor simple para hacer el oscilador, donde R1 y R2 cumplen las mismas funciones que en el circuito del oscilador resonante serie, con dos capacitores en la realimentación, que componen la capacidad de carga y en conjunto con el cristal darán lugar a la frecuencia a la cual oscilará el circuito.
O sea que ajustes en los capacitores de carga, darán lugar a una variación pequeña en la frecuencia de oscilación, permitiendo un ajuste fino de la misma. El cristal es resonante paralelo, especificado para trabajar con una determinada capacidad de carga a la frecuencia deseada y con la tolerancia y estabilidad deseadas. La capacidad de carga para el cristal en este circuito puede ser calculada con la siguiente fórmula:
![]()
donde para inversores de las familias lógicas CMOS de alta velocidad:
Cs es la capacidad parásita del circuito y normalmente se estima entre 3pf a 10pf.
R1 es del orden de 8.2 Mohm a 10 MOhm
R2 es del orden de 470 Ohm a 2200 Ohm
CAPACIDAD DE SER CARGADO (PULLABILITY)
Son los cambios de frecuencia de un cristal, ya sea de su frecuencia de resonancia natural Fr a una frecuencia FL de una carga resonante, o desde una carga resonante a otra. Esta cantidad depende de la capacidad en paralelo Co, de la C1 del cristal y la CL de carga.
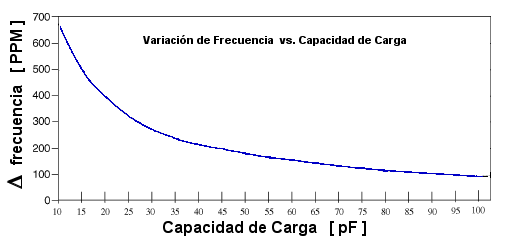
En la siguiente figura se muestra la variación de frecuencia en función de la capacidad de carga, expresada en PPM.
OSCILADORES
Osciladores De Cristal
EN LA ASIGNATURA DE ELECTRÓNICA DIGITAL
UNIVERSIDAD DEL NORTE
PROGAMA DE INGENIERIA ELECTRICA
NOVIEMBRE 29 DEL 2001
CONCLUSIONES
En el presente trabajo se ha experimentado la importancia de los osciladores y en particular de los osciladores de cristal, y su uso en los micrófonos, agujas fonocaptoras, altavoces etc... Auque cada uno de los cristales presentan diferentes características todos son utilizados para propósitos específicos.
Se presentaron diferentes graficas del comportamiento de los cristales entre uno de ellas se mostró la influencia de la temperatura en la frecuencia. Se concluye la importancia de conocer los valores de las capacitancias Co y Cm para describir el funcionamiento a diferentes frecuencias.
1
Descargar
| Enviado por: | Billy |
| Idioma: | castellano |
| País: | Colombia |
