Física
Ondas
ONDAS
<<Concepto de Ondas>>
La definición más general establece que la onda consiste en una perturbación que se propaga con una determinada dependencia espacio-temporal. La perturbación de una magnitud física consiste a menudo en una variación periódica y sobre todo oscilatoria ( repetición entre valores extremos opuestos) por lo que, en particular, la onda se considera como la propagación de una vibración originada en un punto. Existe una amplia variedad de magnitudes físicas cuya oscilación con el tiempo se propaga en el espacio constituyendo ondas. Asimismo pueden ser muy diferentes los mecanismos de transmisión entre un punto y otro. Veamos en un caso particular como es la propagación del desplazamiento vertical de un punto en una cuerda tensa
Perturbación en una cuerda tensa.
Para estudiar la onda como propagación de una perturbación, partimos de una cuerda en equilibrio sometida a cierta tensión por lo que todos sus puntos están inicialmente en línea recta.
Si sobre un punto, tal como su extremo izquierdo, provocamos un desplazamiento 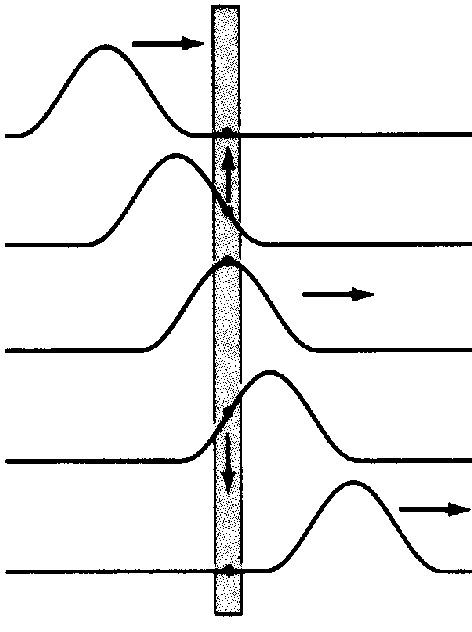
vertical introducimos una perturbación que se transmite debido a las propiedades elásticas de la cuerda. En consecuencia se produce desplazamiento en los puntos adyacentes. Posteriormente este punto vuelve a su estado inicial a la vez que los puntos siguientes después de alcanzar el máximo hacen lo mismo y así sucesivamente.
Observamos que el movimiento realizado por el punto inicial se repite en cada punto de la cuerda, o lo que es equivalente, la perturbación original se propaga sin retorno al suponer una longitud indefinida.
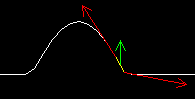
Para analizar el mecanismo responsable de esta propagación seleccionemos un elemento de cuerda con su tensión en ambos extremos y veamos cómo realiza el movimiento vertical al ser alcanzado por la perturbación.
La llegada de la perturbación a su extremo cambia la dirección de la tensión, entonces la fuerza resultante es prácticamente en dirección vertical y origina el desplazamiento en esa dirección del elemento inicialmente en reposo.
<<Aspectos Matemáticos>>
Independientemente del caso particular de onda, podemos deducir el tipo de función matematica que representa la propagación de la onda si observamos como se desplaza un pulso en una cuerda tensa.
Movimiento del pulso en una cuerda.
Un pulso es una onda de duración relativamente corta que suponemos generada en un punto de la cuerda llamado FOCO. 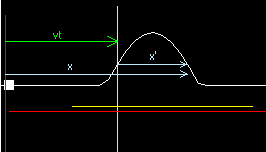
Supongamos una cuerda tensa donde se genera un pulso propagandose de izquierda a derecha con velocidad v respecto a un sistema de referencia fijo X,Y (ejes rojos) que en el instante t=0 esta representado por la ecuacion y=f(x). Supongamos un nuevo sistema coordenado X', Y' (ejes amarillos) que se mueve horizontalmente con la misma velocidad que el pulso.
En el nuevo sistema de referencia el pulso es estacionario, es decir, independiente del tiempo por tanto su ecuacion será
y' = f(x')
Congelando la figura, siendo vt el desplazamiento relativo, podemos vincular en cualquier instante las coordenadas entre ambos sistemas
y' = y x' = x - vt
Por tanto el desplazamiento de un punto de la cuerda en el sistema fijo y por ser igual al y' puede escribirse como
y = f(x-vt)
y esta es la función que representa la onda moviéndose hacia la derecha.
El mismo razonamiento aplicado a un pulso que se mueve hacia la izquierda conduce a
y= f(x+vt)
Podemos sacar como conclusión que cualquier función dependiente de x+vt o x-vt corresponderá una onda propagándose. La onda viajera se representa por la FUNCION DE ONDA que tiene este tipo de dependencia con la posición y el tiempo.
A la ecuación que cumple la función de ondas se debe llegar partiendo de las ecuaciones que rigen el comportamiento de la perturbación en cada caso particular. Obtenemos un modelo general de la ecuación de onda en el caso de la cuerda planteando la 2ª Ley de Newton para el movimiento de alguno de sus puntos
Ecuación de movimiento del elemento de cuerda.
El análisis matematico de una ecuacion de movimiento tiene como punto de partida la 2ª Ley de Newton. Este problema típico de la dinámica lo planteamos para un elemento de la cuerda alcanzado por el pulso con ayuda de la simulación:
La representación de la onda continua que se propaga en una cuerda, nos muestra como evoluciona con el tiempo el desplazamiento de sus puntos desde la posición de equilibrio. El movimiento vertical de cualquier elemento infinitesimal esta originado por la fuerza resultante de las tensiones en ambos extremos, en una aproximación para pequeños desplazamientos. Esta fuerza tiene por tanto solo componente vertical y para estudiar el fenómeno debemos plantear que su valor es igual a la masa por aceleración en el elemento considerado.
La siguiente figura permite amplificar una situación para analizar las fuerzas que actúan en cierto instante sobre un elemento de longitud infinitesimal. Supongamos éste comprendido entre las abcisas x y x+Dx
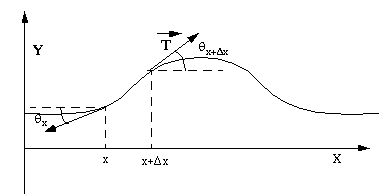
El valor de su desplazamiento viene dado por la coordenada vertical y, por consideraciones geométricas, se obtiene que la fuerza vertical, para ángulos suficientemente pequeños, es
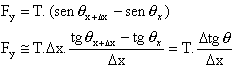
Si utilizamos el concepto de derivada como límite de un cociente de incrementos y la tangente como derivada de la funcion, obtenemos que esa fuerza se puede escribir como
![]()
Suponiendo que la cuerda posee una masa por unidad de longitud m, la masa del elemento bajo estudio es mDx, y considerando la aceleración como derivada segunda del desplazamiento respecto al tiempo, la aplicacion de la 2ª ley de Newton nos lleva a escribir la ecuación de movimiento como
![]()
Simplificando obtenemos que el desplazamiento de cualquier punto de la cuerda cumple una ecuación de la forma
![]()
A este modelo de ecuación lineal (debido a que la función y sus derivadas se presentan solo en primera potencia) deducida para ángulos pequeños, le llamamos ECUACION DE ONDAS y sus soluciones particulares nos dan expresiones de la FUNCION DE ONDA.
La magnitud fisica que corresponde a la función de onda en el caso de cuerdas es el desplazamiento vertical y en la ecuación de onda vemos que la aceleración de un elemento ![]()
esta relacionada con el grado de curvatura de la cuerda ![]()
.
La ecuación de onda constituye una predicción teórica de la existencia de ondas en un sistema. Una función de onda debe ser tal que sus derivadas segundas respecto al espacio y al tiempo coinciden salvo en un factor que depende de las propiedades del medio donde se propaga la onda.
Una onda viajera función de (x-vt) o (x+vt) satisface la ecuación anterior y el factor de proporcionalidad dependiente del medio (T/m) esta relacionado con la VELOCIDAD DE PROPAGACION de la onda como podemos demostrar.
La ecuación de ondas tiene múltiples soluciones y por ser lineal las combinaciones lineales de soluciones particulares por el PRINCIPIO DE SUPERPOSICION también son soluciones de la ecuación.
<<Características de las Ondas>>
Una forma habitual de introducir los parámetros que intervienen en la descripción de ondas es a partir de una definición previa y justificar su significado posteriormente en la función de onda. Algunos términos son ya conocidos de etapas previas, por ejemplo amplitud como valor máximo que puede alcanzar la perturbación o la frecuencia como rapidez con que cambia la perturbación en un punto.
Ondas armónicas en una cuerda.
Muchas de las características de las ondas dependen de la forma como se genera la perturbación en el punto origen o FOCO de la onda. Consideremos de nuevo el caso de una cuerda tensa y supongamos que uno de sus puntos - Origen - realiza el movimiento oscilatorio causado por un muelle sujeto a él.
El desplazamiento vertical, se transmite en sucesivos instantes a los puntos vecinos y constituye la onda propagándose en dirección horizontal. A esta onda que se genera durante un tiempo suficientemente largo se le suele llamar TREN DE ONDAS para distinguirla del PULSO.
Dibujando el desplazamiento vertical de todos los puntos de la cuerda y congelando la figura para compararlos en el mismo instante, apreciamos que su valor varía espacialmente como una función seno.
Escogemos un punto de la cuerda para dibujar en él la magnitud y direccion del desplazamiento. Observamos que hay otros puntos con el mismo valor separados por la distancia que se conoce como LONGITUD DE ONDA. Esta longitud mínima entre dos puntos con el mismo estado de perturbacion es la periodicidad espacial de la onda y se representa por landa l.
La función espacial del seno, con un valor máximo que denominamos A -AMPLITUD- , puede escribirse como

La onda en movimiento se obtiene al reemplazar la coordenada x por x-vt de forma que la FUNCION DE ONDA ARMONICA resulta entonces
![]()
donde al argumento![]()
se conoce como FASE de la onda y de su valor depende la magnitud de la perturbación.
Para una posicion x determinada la fase varia respecto al tiempo como podemos ver en una representación temporal. En una cuerda representa al desplazamiento vertical en cada instante si bien en este caso particular también puede representar el movimiento
puntual de masa. Esto, que solo es posible en medios materiales con propiedades elásticas, no da lugar sin embargo a transporte neto de materia cuando la onda se propaga.
Observamos que la nueva gráfica también es un seno, donde se repite el mismo valor en intervalos de tiempo T llamado PERIODO.
Supongamos que el punto observado corresponde a x=0, su desplazamiento
![]()
es un movimiento armónico simple (MAS) que coincide con el que realiza el extremo del muelle descrito por
![]()
Como el elemento de cuerda realiza el MAS con el mismo periodo y amplitud que el muelle, comparando ambas expresiones se obtiene una relaccion entre el periodo y la longitud de onda
![]()
Comprobamos que T es también el tiempo para que un cierto valor de la onda, determinado por la fase , llegue al siguiente punto separado la distancia de una longitud de onda. Esto nos lleva a interpretar la VELOCIDAD DE LA ONDA como aquella con la que recorre una longitud de onda en el tiempo de un periodo
![]()
Por ser la velocidad con que se transmite la fase de la función de onda,se le conce también comoVELOCIDAD DE FASE.
Si introducimos la frecuencia angular o PULSACION como el numero de periodos en dos pi segundos
![]()
y la frecuencia espacial o NUMERO DE ONDAS como el numero longitudes de onda en dos pi metros
![]()
la función de onda puede escribirse como
![]()
Basándonos en todas estas relaciones y siguiendo con la onda armónica en una cuerda podemos llegar a establecer, de una manera general, cual es la energia transmitida por la onda.
<<Clases de Ondas>>
Aunque todas las ondas tienen unas caracteristicas generales comunes podemos ver algunos aspectos que permiten agruparlas en clases distintas. Cada uno de ellos da lugar a un determinado tipo de onda.
Asi, por ejemplo, atendiendo a su naturaleza la onda puede precisar o no un medio material para su propagacion, esto las agrupa respectivamente en ONDAS MECÁNICAS ( ej. sonido, ondas en cuerdas... ) y en ONDAS ELECTROMAGNÉTICAS ( por ej. la luz se puede propagar en el vacio ).
Dependiendo de cómo se generan, es decir de la forma de oscilar en el origen, tendremos ONDAS PERIÓDICAS o NO PERIÓDICAS. Dentro de las primeras se encuentran las ONDAS ARMÓNICAS que corresponden a vibraciones de tipo senoidal.
Podemos incluir una subdivision segun sea la dependencia espacial de la funcion de onda y tendremos ondas que se propagan en una, dos o tres dimensiones.
Otra consideracion espacial se puede hacer atendiendo a la forma del FRENTE DE ONDAS que es la superfie definida por los puntos del medio a los que llega la perturbacion en el mismo instante. Los frentes de onda mas conocidos corresponden a superficies esfericas, cilindricas y planas, estando todos sus puntos con el mismo valor de la fase
La ONDA PLANA cuyo frente de ondas es un plano, es la mas utilizada por ser una buena aproximacion de cualquier frente en puntos alejados del origen. Su funcion de onda depende de una dimension por tanto por tanto corresponde al modelo básico de estudio.
Otra clasificación que hace referencia a aspectos menos controlables pero de gran importancia por sus consecuencias, es la de ONDAS TRANSVERSALES y ONDAS LONGITUDINALES. En el primer caso la vibracion asociada a la perturbación tiene lugar en una direccion perpendicular a la de propagación de la onda y en el segundo ambas direcciones coinciden. Las ondas transversales pueden ser polarizadas, es decir, el medio puede imponer una de las posibles direcciones perpendiculares de vibracion y eso las distingue de las longitudinales. Las ondas electromagneticas son siempre transversales pero las ondas elásticas, dependiendo del medio en que se propaga, pueden ser de ambas clases. Por ejemplo el sonido es producido por variaciones de presion tranversales y longitudinales en solidos, pero solo longitudinales en liquidos y gases.
Ondas transversales y longitudinales.
Las variaciones en el desplazamiento de los puntos de una cuerda tensa constituyen una onda tipicamente transversal.
El desplazamiento de sus puntos es perpendicular a la dirección de propagación en cualquier instante. En este caso coincide la representacion de la funcion de onda con el aspecto que presenta la cuerda.
Manteniendo una traza comparamos la magnitud del desplazamiento en instantes sucesivos y se aprecia el avance de la onda. Transcurrido un tiempo la persistencia de la traza muestra como todos los puntos pasan por todos los estados de vibración.
Sin embargo para conocer como cambia el desplazamiento con el tiempo resulta mas práctico observar otra gráfica que represente el movimiento de un punto.
Los puntos en fase con el seleccionado vibran a la vez y estan separados por una longitud de onda. La velocidad con que se propaga la fase es el cociente entre esa distancia y el tiempo que tarda en llegar.
Cualquier par de puntos del medio en distinto estado de vibracion estan desfasados y si la diferencia de fase es 90º diremos que estan oposición. En este caso los dos puntos tienen siempre valor opuesto del desplazamiento como podemos apreciar en el registro temporal.
Este tipo de onda transversal igualmente podría corresponder a las vibraciones de los campos electrico y magnético en las ondas electromagnéticas. Una onda electromagnética que puede propagarse en el espacio vacio no produce desplazamientos puntuales de masa.
Las espiras de un muelle (vistas de perfil) pueden realizar oscilaciones en la direccion del eje que pueden constituir una onda longitudinal.
Las vibraciones de una sección producen sucesivos desplazamientos horizontales que se transmiten en dirección paralela .
La funcion de onda representa como cambia el desplazamiento horizontal de cualquier sección conforme transcurre el tiempo. Una espira en particular realiza un movimiento e igualmente las secciones que estan en fasecon ella.
En el muelle se observan compresiones y estiramientos que son mas acusados para mayor amplidtud. Igualmente al aumentar la frecuencia en el mismo muelle se produce un mayor numerode compresiones.
Estas apreciaciones son mas evidentes si lo que se transmite es un pulso de onda.
Descargar
| Enviado por: | Javiergr_uy |
| Idioma: | castellano |
| País: | Uruguay |
