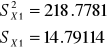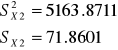Estadística
Muestreo estratificado aleatorio simple
MUESTREO ESTRATIFICADO- M.A.S. (S.R.)
Objetivo:
Estimar el monto de la venta total de pletinas y varillas de cobre entre los meses de enero y setiembre del año 2004 de la empresa D&M Industrial S.A.C.
Población Objetivo:
Clientes de la empresa D&M Industrial S.A.C.
Característica de interés:
Ventas de pletinas y varillas de cobre (monto en soles) de la empresa D&M Industrial S.A.C.
Método de Muestreo:
Usaremos la técnica de muestreo estratificado con muestreo aleatorio simple sin reemplazamiento.
Variable Principal:
Y: Montos de ventas por factura o boleta de los meses de enero a setiembre del presente año.
Variable Auxiliar:
En este caso vemos que existe una relación entre los pesos de pletinas y varillas de cobre con su precio y por ende con el monto total de la factura o boleta. Entonces, la variable auxiliar sería:
X: Peso total de las pletinas o varillas de cobre por factura o boleta.
Marco Muestral:
Registro de ventas de la empresa D&M Industrial S.A.C. desde el mes de enero a setiembre del año 2004.
Unidad de Muestreo:
Cada factura de la empresa emitida entre los meses de enero y setiembre del presente año.
Tabulación de datos:
Emplearemos el método de Sturges, para ello trabajaremos con los datos de la variable auxiliar X.
-
K=1+3.322log(N)
K=1+3.322log(85)
K=7.4095
-
R=Xmáx-Xmín
R=215-2=213
-
A=R/K
A=213/7=30.42"31
-
Re=(A*K)-R
Re = (31*7)-213=217-213=4
-
A=R/K
A=213/8=26.625"27
-
Re=(A*K)-R
Re = (27*8)-213=216-213=3
Luego, elegiremos el número de intervalos (K) que al efectuar el residuo por exceso nos de el menor resultado. Entonces elegimos K=8 en nuestro caso.
Aplicamos el Método de Dalenius:
| Intervalo | f(Y) |
| Acumulada |
| <1;28> | 49 | 7 | 7 |
| [28;55> | 20 | 4.4721 | 11.472 |
| [55;82> | 6 | 2.4495 | 13.9216 |
| [82;109> | 4 | 2 | 15.9216 |
| [109;136> | 3 | 1.7321 | 17.6537 |
| [136;163> | 0 | 0 | 17.6537 |
| [163;190> | 2 | 1.4142 | 19.0679 |
| [190;219> | 1 | 1 | 20.0679 |
Formación de Estratos:
Se formarán 2 estratos de la tabla.
![]()
; se busca el valor más cercano a 10.03395 que es 11.472, entonces tenemos que el primer estrato está formado por el intervalo : <1;55>
10.03395+10.03395=20.06; se busca el valor más cercano a 20.06 que es 20.0679, entonces tenemos que el segundo estrato está formado por el intervalo : [55;219>
Luego, los estratos serán:
| Estrato | Primero | Segundo |
| Límites del estrato | <1; 55> | [55;219> |
| Datos por estrato | N1 = 69 X1 =1426.9
| N2=16 X2=1173.7
|
Datos Poblacionales Estratificados:
| Primer Estrato | |||
| X=pesos | Y=monto | X - Media X | (X - Media X)^2 |
| 2 | 37,89 | -18,6797101 | 348,9315711 |
| 2 | 38,21 | -18,6797101 | 348,9315711 |
| 3,2 | 60,71 | -17,4797101 | 305,5402668 |
| 3,2 | 60,71 | -17,4797101 | 305,5402668 |
| 3,2 | 61,5 | -17,4797101 | 305,5402668 |
| 3,2 | 63,37 | -17,4797101 | 305,5402668 |
| 3,2 | 63 | -17,4797101 | 305,5402668 |
| 3,2 | 63 | -17,4797101 | 305,5402668 |
| 3,2 | 63 | -17,4797101 | 305,5402668 |
| 3,2 | 63 | -17,4797101 | 305,5402668 |
| 4 | 81,07 | -16,6797101 | 278,2127305 |
| 5,7 | 108,5 | -14,9797101 | 224,391716 |
| 5,7 | 108,5 | -14,9797101 | 224,391716 |
| 5,7 | 108,68 | -14,9797101 | 224,391716 |
| 5,7 | 111,5 | -14,9797101 | 224,391716 |
| 6 | 116,14 | -14,6797101 | 215,4938899 |
| 6,4 | 126 | -14,2797101 | 203,9101218 |
| 6,5 | 132,16 | -14,1797101 | 201,0641798 |
| 8 | 154,48 | -12,6797101 | 160,7750494 |
| 8 | 164,65 | -12,6797101 | 160,7750494 |
| 9,6 | 174,18 | -11,0797101 | 122,7599769 |
| 10,8 | 219,47 | -9,87971014 | 97,60867255 |
| 12,1 | 241,14 | -8,57971014 | 73,61142617 |
| 12,8 | 242,57 | -7,87971014 | 62,08983197 |
| 13 | 250,39 | -7,67971014 | 58,97794791 |
| 13 | 251,43 | -7,67971014 | 58,97794791 |
| 13,4 | 265,6 | -7,27971014 | 52,99417979 |
| 13,4 | 272,22 | -7,27971014 | 52,99417979 |
| 13,6 | 249,25 | -7,07971014 | 50,12229574 |
| 13,6 | 263,26 | -7,07971014 | 50,12229574 |
| 15 | 305,34 | -5,67971014 | 32,25910733 |
| 16 | 317,21 | -4,67971014 | 21,89968704 |
| 16,1 | 321,28 | -4,57971014 | 20,97374501 |
| 18,2 | 361,32 | -2,47971014 | 6,148962403 |
| 19,2 | 365,12 | -1,47971014 | 2,189542113 |
| 19,6 | 371,33 | -1,07971014 | 1,165773997 |
| 20 | 376,63 | -0,67971014 | 0,462005881 |
| 20,4 | 381,12 | -0,27971014 | 0,078237765 |
| 21,6 | 430,1 | 0,92028986 | 0,846933417 |
| 22,4 | 390,28 | 1,72028986 | 2,959397185 |
| 22,4 | 434,36 | 1,72028986 | 2,959397185 |
| 22,4 | 443,6 | 1,72028986 | 2,959397185 |
| 24 | 464,85 | 3,32028986 | 11,02432472 |
| 24 | 483,58 | 3,32028986 | 11,02432472 |
| 24,4 | 452,61 | 3,72028986 | 13,84055661 |
| 24,4 | 453,79 | 3,72028986 | 13,84055661 |
| 26,9 | 495,35 | 6,22028986 | 38,69200588 |
| 27 | 471,23 | 6,32028986 | 39,94606385 |
| 27 | 523,4 | 6,32028986 | 39,94606385 |
| 30,5 | 568,81 | 9,82028986 | 96,43809284 |
| 30,5 | 568,81 | 9,82028986 | 96,43809284 |
| 32 | 602,61 | 11,3202899 | 128,1489624 |
| 32 | 612,28 | 11,3202899 | 128,1489624 |
| 32 | 634,26 | 11,3202899 | 128,1489624 |
| 32 | 636,82 | 11,3202899 | 128,1489624 |
| 32,2 | 621,3 | 11,5202899 | 132,7170783 |
| 32,4 | 638,48 | 11,7202899 | 137,3651943 |
| 37,8 | 680,29 | 17,1202899 | 293,1043247 |
| 39 | 754,94 | 18,3202899 | 335,6330204 |
| 40,2 | 700,41 | 19,5202899 | 381,041716 |
| 42,7 | 737,56 | 22,0202899 | 484,8931653 |
| 43 | 760,23 | 22,3202899 | 498,1953392 |
| 43 | 823,96 | 22,3202899 | 498,1953392 |
| 44,7 | 801,3 | 24,0202899 | 576,9743247 |
| 48,3 | 889,42 | 27,6202899 | 762,8804117 |
| 50,3 | 950,52 | 29,6202899 | 877,3615711 |
| 51,2 | 985,91 | 30,5202899 | 931,4880928 |
| 52 | 962,11 | 31,3202899 | 980,9605566 |
| 53,5 | 1066,52 | 32,8202899 | 1077,171426 |
| Total X | Media X | Cuasivar. (X) | Total |
| 1426,9 | 20,6797101 | 218,7781117 | 14876,91159 |
| Segundo Estrato | |||
| X=pesos | Y=monto | X - Media X | (X - Media X)^2 |
| 55,2 | 1015,58 | -75,85625 | 5754,17066 |
| 55,4 | 1021,38 | -75,85625 | 5754,17066 |
| 57,6 | 1072,39 | -74,35625 | 5528,85191 |
| 61 | 1054,74 | -74,35625 | 5528,85191 |
| 64,5 | 1194,09 | -74,35625 | 5528,85191 |
| 80,7 | 1517,97 | -74,35625 | 5528,85191 |
| 83,4 | 1532,52 | -74,15625 | 5499,14941 |
| 84,4 | 1590,84 | -73,95625 | 5469,52691 |
| 104,5 | 2074,29 | -68,55625 | 4699,95941 |
| 107 | 2069,44 | -67,35625 | 4536,86441 |
| 124,6 | 2470,74 | -66,15625 | 4376,64941 |
| 129 | 2548,21 | -63,65625 | 4052,11816 |
| 129 | 2556,84 | -63,35625 | 4014,01441 |
| 172,4 | 3198,47 | -63,35625 | 4014,01441 |
| 178 | 3462,15 | -61,65625 | 3801,49316 |
| 215 | 4144,29 | -58,05625 | 3370,52816 |
| Total X | Media X | Cuasivar. (X) | Total |
| 1701,7 | 106,35625 | 5163,87113 | 77458,0669 |
Cálculo del tamaño de la muestra para un valor especificado de la varianza si Ch es constante:
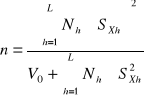
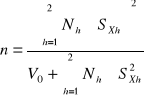
Pero tenemos en cuenta que:
![]()
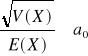
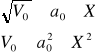
Entonces, para X=3128.6 y un a0 específico se tiene:
| a0 | V0 | n |
| 0.05 | 24 470.3449 | 39 |
| 0.10 | 97 881.3796 | 25 |
| 0.15 | 220 233.1041 | 15 |
Elegimos n=15.
Asignación de los elementos de los estratos en la muestra mediante la asignación de Neyman:

Ahora,reemplazamos los valores hallados en la fórmula:

Muestras aleatorias simples sin reemplazo por estrato:
| Primer Estrato | ||||
| Nº de orden | Nº Aleatorio | Y | Y - Media Y | (Y - Media Y)^2 |
| 1 | 28 | 249,25 | -32,4742857 | 1054,57923 |
| 2 | 52 | 612,28 | 330,555714 | 109267,08 |
| 3 | 13 | 108,68 | -173,044286 | 29944,3248 |
| 4 | 26 | 265,6 | -16,1242857 | 259,99259 |
| 5 | 45 | 453,79 | 172,065714 | 29606,61 |
| 6 | 9 | 63 | -218,724286 | 47840,3132 |
| 7 | 21 | 219,47 | -62,2542857 | 3875,59609 |
| Media Y | Total Y | Cuasivar. (Y) | Total | |
| 281,724286 | 1972,07 | 36974,7494 | 221848,496 |
| Segundo Estrato | ||||
| Nº de orden | Nº Aleatorio | Y | Y - Media Y | (Y - Media Y)^2 |
| 1 | 15 | 4144.29 | 1884,105 | 3549851,65 |
| 2 | 4 | 1194.09 | -1066,095 | 1136558,55 |
| 3 | 5 | 1517.97 | -742,215 | 550883,106 |
| 4 | 2 | 1072.39 | -1187,795 | 1410856,96 |
| 5 | 1 | 1021.38 | -1238,805 | 1534637,83 |
| 6 | 13 | 3198.47 | 938,285 | 880378,741 |
| 7 | 10 | 2470.74 | 210,555 | 44333,408 |
| 8 | 14 | 3462.15 | 1201,965 | 1444719,86 |
| Media Y | Total Y | Cuasivar. (Y) | Total | |
| 2260,185 | 18081,48 | 1507460,02 | 10552220,1 |
Estimaciones para el total poblacional Y:
-
Estimación de Y:
![]()

Nota: Y=59 578.805
-
Estimación de la Varianza:


-
Estimación del C.V.:

El ![]()
estimado es de 12% lo cual nos indica que este método de muestreo es muy acertado para realizar las estimaciones respectivas al total poblacional Y.
-
Intervalo de confianza al 95%:

La empresa D&M Industrial S.A.C. ha tenido una venta total que varía entre los s/.40 941 y s/.70 262 en el período de enero a setiembre del presente año .
MUESTREO ALEATORIO SIMPLE SIN REEMPLAZAMIENTO
Quiero solucionar el mismo problema: ¿Cuánto ha vendido en total,en lo que va del año, la empresa D&M Industrial S.A.C. en cuanto a pletinas y varillas de cobre se refiere?
Mi objetivo es el mismo, pero en ésta oportunidad haremos las estimaciones correspondientes con una técnica de muestreo distinta: Muestreo Aleatorio Simple sin reemplazamiento, para luego comparar cuál de los 2 métodos es mejor de aplicar en este caso.
Variable en estudio:
Y: Montos de ventas por factura o boleta de los meses de enero a setiembre del presente año.
“Y” es una variable cuantitativa contínua.
Datos Poblacionales:
N=85
Y=59 578.56
![]()
Tamaño de muestra:

Para un a0 fijo de 15% y reemplazando los datos poblacionales en la fórmula, se tiene:
n " 34.559 ![]()
n = 35.
Obteniendo la muestra:
| Nº de Orden | Nº Aleatorio | y | y- Media (y) | (y - Media(y))^2 |
| 1 | 35 | 483,58 | -186,884571 | 34925,84304 |
| 2 | 30 | 361,32 | -309,144571 | 95570,36604 |
| 3 | 5 | 680,29 | 9,82542857 | 96,53904661 |
| 4 | 2 | 390,28 | -280,184571 | 78503,39407 |
| 5 | 59 | 823,96 | 153,495429 | 23560,84659 |
| 6 | 25 | 251,43 | -419,034571 | 175589,9721 |
| 7 | 37 | 430,1 | -240,364571 | 57775,1272 |
| 8 | 13 | 242,57 | -427,894571 | 183093,7643 |
| 9 | 10 | 3462,15 | 2791,68543 | 7793507,532 |
| 10 | 44 | 568,81 | -101,654571 | 10333,65189 |
| 11 | 8 | 381,12 | -289,344571 | 83720,28102 |
| 12 | 76 | 250,39 | -420,074571 | 176462,6456 |
| 13 | 60 | 737,56 | 67,0954286 | 4501,796535 |
| 14 | 24 | 263,26 | -407,204571 | 165815,563 |
| 15 | 28 | 63,37 | -607,094571 | 368563,8187 |
| 16 | 20 | 754,94 | 84,4754286 | 7136,098032 |
| 17 | 68 | 1054,74 | 384,275429 | 147667,605 |
| 18 | 53 | 985,91 | 315,445429 | 99505,81841 |
| 19 | 45 | 568,81 | -101,654571 | 10333,65189 |
| 20 | 77 | 376,63 | -293,834571 | 86338,75537 |
| 21 | 31 | 63 | -607,464571 | 369013,2055 |
| 22 | 46 | 1066,52 | 396,055429 | 156859,9025 |
| 23 | 69 | 3198,47 | 2528,00543 | 6390811,447 |
| 24 | 43 | 568,81 | -101,654571 | 10333,65189 |
| 25 | 47 | 2548,21 | 1877,74543 | 3525927,895 |
| 26 | 17 | 464,85 | -205,614571 | 42277,35198 |
| 27 | 3 | 700,41 | 29,9454286 | 896,7286923 |
| 28 | 61 | 111,5 | -558,964571 | 312441,3921 |
| 29 | 67 | 154,48 | -515,984571 | 266240,078 |
| 30 | 32 | 219,47 | -450,994571 | 203396,1035 |
| 31 | 83 | 317,21 | -353,254571 | 124788,7922 |
| 32 | 74 | 495,35 | -175,114571 | 30665,11313 |
| 33 | 38 | 305,34 | -365,124571 | 133315,9527 |
| 34 | 11 | 60,71 | -609,754571 | 371800,6374 |
| 35 | 15 | 60,71 | -609,754571 | 371800,6374 |
| Media(y) | y | Cuasivar.(y) | Total | |
| 670,464571 | 23466,26 | 644516,8223 | 21913571,96 |
Estimación del Total:

= 670.4646
![]()
Estimación de la Varianza:
V![]()
= 78 262 756.99
Estimación del C.V.:
C.V (![]()
) = 
El C.V. estimado de ![]()
es de 16.5% , lo cual indica que esta técnica es buena para hacer las estimaciones correspondientes.
Estimación del total poblacional por intervalo de confianza al 95%:

La venta total en cuanto a pletinas y varillas de cobre, en el período enero-setiembre del 2004, de la empresa D&M Industrial S.A.C. se encuentra entre los s/.39 650 y s/.74 328.
C O N C L U S I O N E S
-
Hemos analizado el mismo problema pero con 2 técnicas distintas de muestreo.
-
Con el MAS (SR) hemos obtenido buenas estimaciones y con el muestreo estratificado(mas-sr) también .Pero comparando ambos métodos nos damos cuenta que el muestreo estratificado con mas(sr) nos da una mejor aproximación del total de ventas que el mas (sr) y esto lo vemos claramente en la amplitud de los respectivos intervalos de confianza , el de muestreo estratificado tiene una menor amplitud.
-
La pregunta es ¿podemos trabajar directamente con mas(sr)?,la respuesta es si, tengo una buena estimación del total en este caso,.
-
¿Puedo emplear un muestreo estratificado para este caso?, la respuesta es no, porque si bien obtengo un mejor resultado, gastaría más tiempo y dinero para encontrar la variable auxiliar y luego para encontrar los valores muestrales.
-
En general puedo usar un muestreo estratificado siempre que no conozca mi variable principal o en caso contrario que ésta sea muy heterogénea.
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | Perú |