Matemáticas
Modelo matemático de Lotka-Volterra
Modelo matemático Lotka-Volterra.
El matemático italiano Volterra, después de haberse interesado por la ecología matemática y haber sido estimulado por su amigo zoólogo Humberto D' Ancona, estudio los registros de las pesquerías del Mar Adriático Superior y observó que, durante y después de la Segunda Guerra Mundial, cuando la pesca había disminuido drásticamente, la proporción de los depredadores había aumentado.
Este hecho lo llevo a estudiar ese problema de una manera más general, logrando construir la primer teoría determinista sistematizada de la dinámica de poblaciones.
-
Oscilaciones en las relaciones presa-depredador de Volterra.
Para iniciar su investigación matemática estableció ciertas cosas:
Que la especie depredadora se alimentaba exclusivamente de la especie presa, mientras que ésta se alimentaba de un recurso que se encontraba en el hábitat en grandes cantidades, el cual solo intervenía así ( pasivamente).
Que ambas poblaciones eran homogéneas, es decir, no intervenían factores como la edad o el sexo.
Que, así mismo, el medio era homogéneo, es decir, que las características físicas, biológicas entre otras, eran las mismas en el hábitat.
Y que los encuentros de la especie depredadora con las especie presa eran igualmente probables.
Siendo así, se encontró con que solo existían dos variables : el tamaño poblacional de la especie depredadora y el de la especie presa. Así mismo, supuso que ambos tamaños poblacionales dependían exclusivamente del tiempo y no de alguna otra variable especial.
Determino que si no existiesen depredadores, la población de presas crecería malthusianamente , es decir:
![]()
mientras que si ni hubiese presas, la especie depredadora decrecería, también siguiendo un modelo maltusiano, es decir:
![]()
Ahora bien, dado que la interacción beneficia a la especie depredadora y perjudica a la presa, él supuso que seria necesario modificar a los depredadores en un termino que diera cuenta del perjuicio para una y del beneficio para la otra, lo que tendría que ser :

Luego entonces, Volterra se topo con el problema de encontrar una forma analítica para cada termino que aparece entre corchetes y, basándose en el argumento de que cuantos más encuentros por unidad de tiempo haya entre individuos de la especie presa con la especie depredadora, mayor ha de ser el perjuicio de unos y el beneficio de otros; llego a la conclusión de que el numero de encuentros por unidad de tiempo entre presas y depredadores, es proporcional al producto algebraico de sus respectivas densidades poblacionales, es decir:
[Numero de encuentros por u. de t.] x(t)y(t)
He incorporó esto en las dos ecuaciones anteriores :
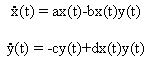
donde a es la tasa instantánea de aumento de presas en ausencia de depredadores; mientras que c es la tasa instantánea per capita de disminución de ,depredadores en el caso de ausencia de presas. Originalmente Volterra interpreto esto diciendo que :
“...los parámetros constantes a y c representan la razón de nacimiento y muerte de las dos especies; mientras que b mide la susceptibilidad de la especie presa a la depredación y d mide la habilidad de depredación de esta especie. Las constantes b y d son la proporción de encuentros perjudiciales para las presas y la correspondiente de encuentros benéficos para los depredadores, respectivamente...”
Y así logro afirmar que en una interacción presa-depredador descrita en las ecuaciones anteriores, el tamaño de la especie presa y el de la especie depredadora, cambian periódicamente al aumentar el tiempo lo que en términos geométricos sería: *La dinámica de las presas.-
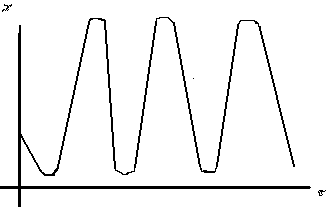
t
*La dinámica de los depredadores.-
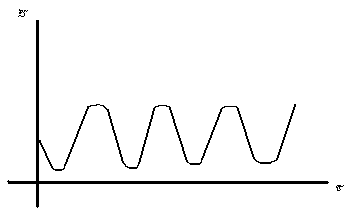
Volterra, basándose en esto, formulo la ley que posteriormente se llamaría Ley de la periodicidad de Volterra, la cual dice que “el cambio de los tamaños poblacionales de ambas especies (presa y depredadora) son periódicos y el periodo depende solamente de a, b, c y d del tamaño inicial de las dos especies...”. Para el caso de pequeñas oscilaciones Volterra da como periodo T=2 / ac.
Posteriormente, formuló otras dos leyes relacionadas a su modelo presa-depredador, las cuales son :
Su Ley de Conservación de los Promedios. Según ésta los promedios de los tamaños poblacionales de la especie presa y de la depredadora son independientes de su tamaño inicial y, calculados en un periodo son, respectivamente :
X = c/d y y = a/b
Ley de la perturbación de los promedios. Ésta dice que si las poblaciones de ambas especies son destruidas a una razón proporcional a su tamaño poblacional, el promedio de las presas aumenta; mientras que el de los depredadores disminuye
Ésta ultima ley es conocida como El principio de Volterra y tiene importantes implicaciones en el uso de insecticidas que destruyen tanto a los insectos depredadores como a sus insectos presa. Es decir , si la proliferación de una plaga (presas) es controlada mediante procedimientos naturales por otra especie (depredadores) , existe cierto equilibrio entre ambas. Si, por otro lado, en cierto momento se decide la aplicación de un insecticida para acabar con la plaga sin tomar en cuenta que éste también mata a los depredadores; el resultado será- según el Principio de Volterra- que, en promedio, la plaga aumenta y, también en promedio, la especie con la que se controlaba disminuye.
-
Modelo de presa-depredador de Volterra con limitaciones de recursos para la presa.
Partiendo del modelo clásico de Volterra, desde un punto de vista cualitativo, se puede obtener un modelo para el cual la especie presa se alimente de un recurso existente en el ecosistema en cantidades limitadas, es decir, sería un modelo más realista que el anterior en el cual se considera que la especie presa se alimenta de un recurso existente en el ecosistema en grandes cantidades. Luego entonces el modelo sería :
x(t) = ax(t)-(t)-bx(t)y(t) = f(x,y)
y(t) = -cy(t)+dx(t)y(t) = g(x,y)
Así, es necesario definir en primer lugar a y , como:
= {(x,y) a-Ex-by = 0} y = {(x,y) -c+dx=0}
donde los puntos de equilibrio son :
P = (0,0), P = (a/E,0) y P = (c/d,ad-cE/bd) = (x*,y*)
Y dependiendo de la disposición relativa de las rectas y será que el punto P tenga o no sentido, para lo cual hay tres posibilidades :
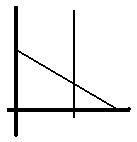
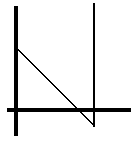
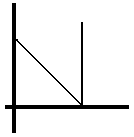
Para realizar un modelo de coexistencia, los dos ultimos quedan excluidos, es decir, el único util es aquél en el que la razon c/d es estrictamente menor que la capacidad de carga, a/E, de las presas en ausencia de los depredadores. Para obtener el comportamiento de las densidades poblacionales de presas y depredadores al transcurrir el tiempo en el caso de que el estado inicial sea cercano a los puntos P , P , P ; se recurre a realizar una linealización y después de varios operaciones se concluye que los tamaños poblacionales de presas y depredadores oscilan con amplitud decreciente tendiendo a x* y y* , respectivamente.
Así, se puede deducir que si (ad-cE) > 0 entonces la coexistencia entre presas y depredadores cuya dinamica está descrita por el sistema anterior, se da a través de la existencia de un atractor global.
-
Oscilaciones en modelos generales de Lotka-Volterra para dos especies.
Posteriormente , se llego a un sistema que generaliza los dos modelos anteriores, es decir :
x(t) = [b +a x(t)+ a y(t)]x(t)
y(t) = [b + a y(t)] y(t)]y(t)
donde dependiendo los signos que tengan los coeficientes a , seran los tipos de interacciones entre las dos especies.
Este modelo presenta la peculiaridad de que a través de él no puede ser modelada la coexistencia entre dos especies por medio de comportamientos aislados, es decir, tal sistema no posee ciclos limites.
BIBLIOGRAFÍA.-
-
Gutiérrez Sánchez, Luis, Matemáticas para las ciencias naturales, Sociedad Matemática Mexicana ,México, 1998, p.p. 529-550.
-
Derrick, William, Ecuaciones diferenciales con aplicaciones, Fondo Educativo Interamericano, México, 1984, p.p. 297-299.
Descargar
| Enviado por: | Dark Ravnos |
| Idioma: | castellano |
| País: | México |
